【NOIP2017】跳房子

这题我0分。

比赛时，我一眼出正解，哈哈，太水了！

这题不就是一个二分+DP+单调队列吗？

然而，细节决定成败。

我错了许多细节，就挂了。

我只考了0分。。。

首先，这题满足一个条件：

保证g变大后，如果原来满足条件，现在也会满足条件；而如果原来不满足条件，现在就有可能满足条件。

g变小后，如果原来满足条件，现在不一定会满足条件；而如果原来不满足条件，现在就一定不可能满足条件。

所以，我们可以用二分找出最合适的g的值。

已知，\({0\leq g\leq 10^9}\)，且跳跃的范围是 Max(1,d-g) ~ d+g。

我们就可以列出状态转移方程了：$${F_i=max(F_j)+S_i\space\space\space(X_j+a\leq X_i \bigwedge X_j+b\geq X_i)}$$

其中，a为跳跃最短距离，b为跳跃的最长距离。

这样做的时间复杂度是\({O(log_210^9n^2)}\)，很明显会时超50分。

所以，我们就要把DP优化一下了。

我们很容易发现，状态转移方程中，对于不同的i，\({max(F_j)}\)的值可能是一样的，但我们的程序却会从一个较大的区间 上一次最后一个 找到的位置+1 ~ i-1 中找 ，这就是程序中最耗时的地方。

怎么优化呢？

我们有多种优化方式，其中我推荐两种：大根堆，还有单调队列。大根堆码量大，而单调队列方便快捷，因此我比较喜欢用单调队列。

用\({queue_i}\)表示单调队列的第i个元素，用head表示单调队列中有效范围内的第一个元素的下标，用tail表示单调队列中有效范围内的最后一个元素的下标。

单调队列存的是元素的下标，即\({F_i}\)，\({X_i}\)中的 i ，这样能方便判断。

由于这个单调队列是递减的（即第一个元素最大，第二个元素比第一个小，第三个比第二个小……最后一个是最小的），所以我们每次使用的最大值就是单调队列中有效范围内的第一个元素对应的值。

那么我们的状态转移方程就可以变成这个样子了：$${F_i=F_{queue_{head}}+S_i\space\space(X_{queue_{head}}+a \leq X_i \bigwedge X_{queue_{head}}+b \geq X_i)}$$

其中，a为跳跃最短距离，b为跳跃的最长距离。

这样用起来是很方便的，但是，重点来了——

怎样才能保持单调队列的单调性（使单调队列递减）和有效性（使\({(X_{queue_{head}}+a \leq X_i \bigwedge X_{queue_{head}}+b \geq X_i)}\)）呢？

首先，我们每一次加入元素时，如果 （new是新加入的元素），也就是说这个样子（越高的值越大）：

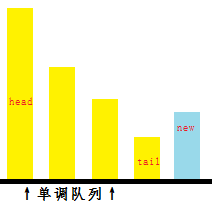
许多人都会认为要变成下面这个样子：

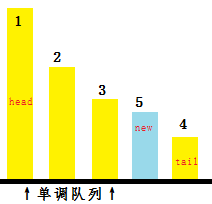
第i个柱子上面的数字是X[queue[i]]的值。

由于新加入单调队列的数，都是可以跳到第i个格子上的，即\({X_{new}+a\leq X_i\bigwedge X_{new}+b\geq X_i}\)

而X又是递增的，所以\({X_{new}+a\leq X_i\leq X_{i+1}\leq X_{i+2}\cdots X_n}\) 。

但是从5（\({X_{new}}\)）这个位置出发，能跳到的最远距离绝对比4远，所以当5不能跳到某一个地方时，4也绝对跳不到那个位置。所以4就没用了。

因此我们可以把4删掉（即tail-1），最后再把5加入，变成下面这个样子：

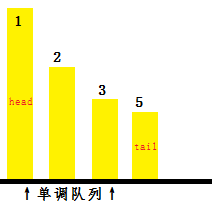
有时候我们要删除很多元素，如下面这个例子：



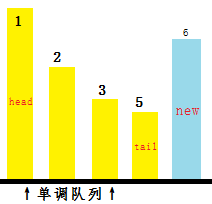
变成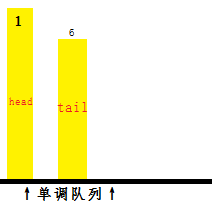

我们就要用一个while循环来删除F值小于等于F[new]的数。

---

但我们的queue[head]是会过期的（queue[head]跳不到第i个格子），这时我们的queue[head]就不能用了。

我们要删掉queue[head]，怎么删掉呢？直接head+1就好了。

最后一点，建议同学们把不能到达的点的F赋值为-maxlongint！

---

#include<cstdio>
using namespace std;
#define maxlongint 1999999999
int f[500001],queue[500001],x[500001],s[500001];
int main()
{
	freopen("jump.in","r",stdin);
	freopen("jump.out","w",stdout);
	int n,d,k,l=0,r=1000000000,mid,i,j,t,ans=-1,maxx,minn,head,tail,last;
	bool bk,bz;
	scanf("%d%d%d",&n,&d,&k);
	for(i=1;i<=n;i++) scanf("%d%d",&x[i],&s[i]);
	l=0;r=1000000000;
	while(l<=r)
	{
		mid=(l+r)/2;
		maxx=d+mid;bk=false;bz=true;
		minn=d-mid;last=0;
		if(minn<1) minn=1;
		tail=head=1;
		queue[1]=0;
		for(i=1;i<=n;i++)
		{
			if(maxx>=x[i]&&minn<=x[i])
			{
				bz=false;
				break;
			}
		}
		if(bz)
		{
			l=mid+1;
			continue;
		}
		for(i=1;i<=n;i++)
		{
			f[i]=maxlongint;
			for(j=last+1;j<i;j++)
			{
				if(x[j]+minn>x[i]) break;
				if(x[j]+maxx<x[i]) continue;
				last=j;
				if(f[j]==maxlongint) continue;
				while(head<=tail&&f[queue[tail]]<=f[j]) queue[tail--]=0;
				queue[++tail]=j;
			}
			while(head<tail&&x[queue[head]]+maxx<x[i]) head++;
			if(x[queue[head]]+maxx<x[i]||x[queue[head]]+minn>x[i]) f[i]=maxlongint;
			else f[i]=f[queue[head]]+s[i];
			if(f[i]<maxlongint&&f[i]>=k)
			{
				bk=true;
				break;
			}
		}
		if(bk)
		{
			ans=mid;
			r=mid-1;
		}
		else l=mid+1;
	}
	printf("%d\n",ans);
	return 0;
}