mod 运算与乘法逆元
mod 运算与乘法逆元
%运算
边乘边mod
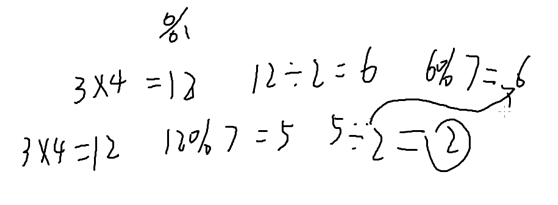
乘法 除法 mod
希望计算5/2%7=6
乘法 除法 mod
希望计算5/2%7=6
两边同时/x
在取mod(p)运算下，a/b=a*bp-2
bp-2 =1/b
bp-2 是b的乘法逆元
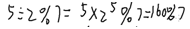=6
P3811 P1082
P不为素数
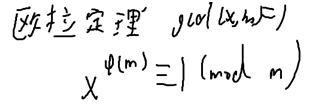
Φ（m）欧拉函数：
1— m中有多少个数和m互质
Φ（p）= p-1
当m不是质数的时候
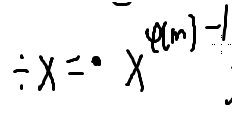
暴力：
题目让干啥就干啥
暴力是个技术活 (shang ke bu nu li ,bao li chu qi ji)
mod 运算与乘法逆元的更多相关文章
- Light OJ 1067 Combinations (乘法逆元）
Description Given n different objects, you want to take k of them. How many ways to can do it? For e ...
- $O(n+log(mod))$求乘法逆元的方法
题目 LOJ #152. 乘法逆元 2 题解 一个奇技淫巧qwq.可以离线求乘法逆元,效率\(O(n+log(mod))\). 考虑处理出\(s_n\)表示\(\prod_{i=1}^na_i\).以 ...
- HDU 1576 (乘法逆元)
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=1576 题目大意:求(A/B)mod 9973.但是给出的A是mod形式n,n=A%9973. 解题思 ...
- Hdu 1452 Happy 2004（除数和函数，快速幂乘（模），乘法逆元）
Problem Description Considera positive integer X,and let S be the sum of all positive integer diviso ...
- A. On The Way to Lucky Plaza 概率 乘法逆元
A. On The Way to Lucky Plaza time limit per test 1.0 s memory limit per test 256 MB input standard i ...
- 数论入门2——gcd,lcm,exGCD,欧拉定理,乘法逆元,(ex)CRT,(ex)BSGS,(ex)Lucas,原根,Miller-Rabin,Pollard-Rho
数论入门2 另一种类型的数论... GCD,LCM 定义\(gcd(a,b)\)为a和b的最大公约数,\(lcm(a,b)\)为a和b的最小公倍数,则有: 将a和b分解质因数为\(a=p1^{a1}p ...
- 乘法逆元__C++
在开始之前我们先介绍3个定理: 1.乘法逆元(在维基百科中也叫倒数,当然是 mod p后的,其实就是倒数不是吗?): 如果ax≡1 (mod p),且gcd(a,p)=1(a与p互质),则称a关于模p ...
- 同余and乘法逆元学习笔记
目录 数学符号 快速幂 方法一 方法二 同余 概念 同余的性质 乘法逆元 概念: 求逆元的方法 扩展欧几里得 快速幂法\(o(n*log(n))\) 递推法\(o(n)\) sjp大佬让我写同余那就只 ...
- something about 乘法逆元
before 在求解除法取模问题(a / b) % m时,我们可以转化为(a % (b * m)) / b, 但是如果b很大,则会出现爆精度问题,所以我们避免使用除法直接计算. (逆元就像是倒数一样的 ...
随机推荐
- matplotlib基本函数
数据分析 matlab Numpy + scipy + pandas +matplotlib 数据计算 +科学应用+数据清洗+数据可视化 1 Numpy概述 1 基于c语言的python接口的数值算法 ...
- 怎么制作电脑系统安装U盘？
现如今U盘安装电脑系统已经是非常普遍的一种方式,这种方式简单好用,能应对大多数情况,受到很多用户的欢迎. 雨后清风U盘启动是一款可将普通U盘制作为系统引导启动工具的软件,其制作的U盘启动盘融合了雨后清 ...
- Kinect for Windows SDK开发入门(三)：基础知识 下
原文来自:http://www.cnblogs.com/yangecnu/archive/2012/04/02/KinectSDK_Application_Fundamentals_Part2.htm ...
- linux实操_shell读取控制台输入
基本语法: read [选项] [参数] 选项: -p 指定读取值时的提示符 -t 指定读取值时等待的时间(秒),如果没有在指定的时间内输入,就不再等待了 参数: 变量:指定读取值的变量名 实例1:读 ...
- Strategic game POJ - 1463 【最小点覆盖集】
Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solu ...
- E:only-child
E:only-child 语法: E:only-child { sRules } 说明: 匹配父元素仅有的一个子元素E.大理石机械构件维修 要使该属性生效,E元素必须是某个元素的子元素,E的父元素最高 ...
- javaMail 详解
原文:http://www.matrix.org.cn/resource/article/44/44101_JavaMail.html 一.JavaMail API简介JavaMail API是读取. ...
- [Luogu] 金字塔神话
这是出给pj的题ccccc #include <bits/stdc++.h> #define ll long long #define INF 2147483647 #define y1 ...
- 线段树详解 （原理，实现与应用）（转载自：http://blog.csdn.net/zearot/article/details/48299459）
原文地址:http://blog.csdn.net/zearot/article/details/48299459(如有侵权,请联系博主,立即删除.) 线段树详解 By 岩之痕 目录: 一:综述 ...
- bit,byte,word,bps,Bps,比特,字节,字, 一图看懂