NOIP200606金明的预算方案

试题描述：

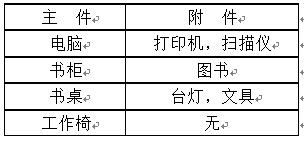
金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过N元钱就行”。今天一早，金明就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：如果要买归类为附件的物品，必须先买该附件所属的主件。每个主件可以有0个、1个或2个附件。附件不再有从属于自己的附件。金明想买的东西很多，肯定会超过妈妈限定的N元。于是，他把每件物品规定了一个重要度，分为5等：用整数1~5表示，第5等最重要。他还从因特网上查到了每件物品的价格（都是10元的整数倍）。他希望在不超过N元（可以等于N元）的前提下，使每件物品的价格与重要度的乘积的总和最大。设第j件物品的价格为v[j]，重要度为w[j]，共选中了k件物品，编号依次为j1，j2，……，jk，则所求的总和为：v[j1]*w[j1]+v[j2]*w[j2]+ …+v[jk]*w[jk]。（其中*为乘号）。请你帮助金明设计一个满足要求的购物单。

输入：第1行，为两个正整数，用一个空格隔开：n  m
（其中N（<32000）表示总钱数，m（<60）为希望购买物品的个数。）
从第2行到第m+1行，第j行给出了编号为j-1的物品的基本数据，每行有3个非负整数v  p  q
（其中v表示该物品的价格（v<10000），p表示该物品的重要度（1~5），q表示该物品是主件还是附件。如果q=0，表示该物品为主件，如果q>0，表示该物品为附件，q是所属主件的编号）

输出：只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值（<200000）。

输入示例：

1000  5
800  2  0
400  5  1
300  5  1
400  3  0
500  2  0

输出示例：

2200

解题思路：

还是DP

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int dp[],p[],v[],p1[],v1[],p2[],v2[];
int ans;
int main()
{
    int n,m;
    cin>>m>>n;
    m/=;
    for(int i=;i<=n;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        a/=;
        if(c!=)
        {
            if(p1[c]==)
            {
                p1[c]=a;
                v1[c]=b;
            }
            else
            {
                p2[c]=a;
                v2[c]=b;
            }
        }
        else
        {
            p[i]=a;
            v[i]=b;
        }
    }
    for(int i=;i<=n;i++)
        for(int j=m;j>=p[i];j--)
        {
            dp[j]=max(dp[j],dp[j-p[i]]+v[i]*p[i]);
            if(j-p[i]-p1[i]>=) dp[j]=max(dp[j],dp[j-p[i]-p1[i]]+v[i]*p[i]+v1[i]*p1[i]);
            if(j-p[i]-p2[i]>=) dp[j]=max(dp[j],dp[j-p[i]-p2[i]]+v[i]*p[i]+v2[i]*p2[i]);
            if(j-p[i]-p1[i]-p2[i]>=) dp[j]=max(dp[j],dp[j-p[i]-p1[i]-p2[i]]+v[i]*p[i]+v1[i]*p1[i]+v2[i]*p2[i]);
            ans=max(ans,dp[j]);
        }
    cout<<ans*;
   // system("pause");
}
//1000 +1200 +1500+2000+1600