跟我学算法聚类(kmeans)

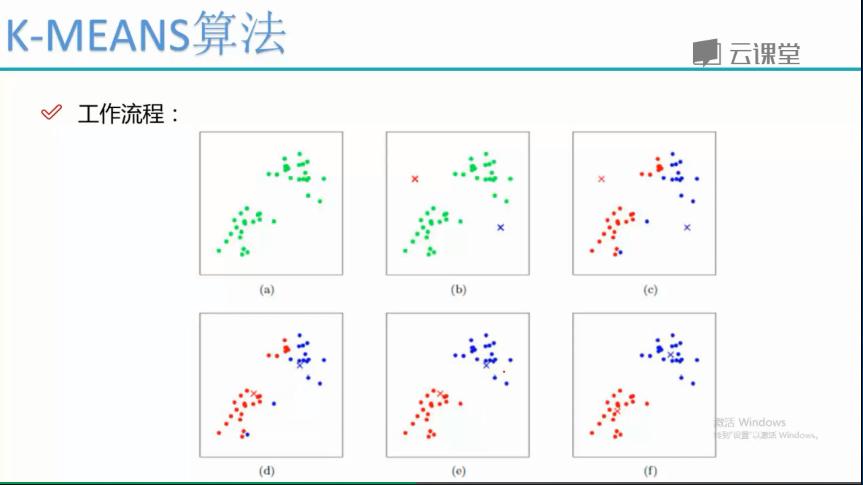
kmeans是一种无监督的聚类问题，在使用前一般要进行数据标准化, 一般都是使用欧式距离来进行区分，主要是通过迭代质心的位置

来进行分类，直到数据点不发生类别变化就停止,

一次分类别，一次变换质心，就这样不断的迭代下去

优势：使用方便
劣势：1.K值难确定

2. 复杂度与样本数量呈线性关系

3.很难发现形状任意的簇

4.容易受初始点的影响

python中使用 sklearn.cluster 模块,使用的时候需要指定参数

第一步：导入数据,提取数据中的变量保存为X

import pandas as pd
beer = pd.read_csv('data.txt', sep=' ')

X = beer[["calories","sodium","alcohol","cost"]]

第二步：进行kmans聚类分析

from  sklearn.cluster import KMeans

km = KMeans(n_clusters=3).fit(X)  #聚成三蔟
km2 = KMeans(n_clusters=2).fit(X) #聚成两蔟

beer['cluster'] = km.labels_    #返回聚类的标签结果
beer['cluster2'] = km2.labels_

beer.sort_values('cluster')  #根据'cluster'进行排序

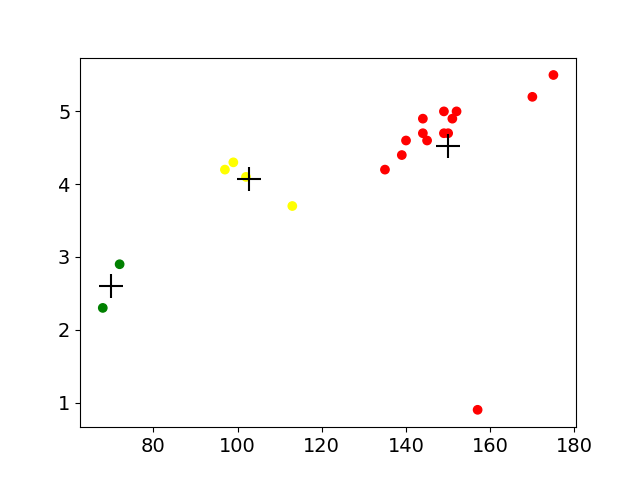
第三步：根据分类结果画出带颜色的散点图，及其混淆矩阵

from  pandas.tools.plotting import  scatter_matrix

cluster_center = km.cluster_centers_

cluster_center_2 = km2.cluster_centers_

# print(beer.groupby('cluster').mean())  #groupby进行快速分组,mean求平均
#
# print(beer.groupby('cluster2').mean())

centers = beer.groupby("cluster").mean().reset_index()  #reset_index()重新添加了序号

import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 14   #rcParams 用于修改字体的大小

import numpy as np
color = np.array(['red', 'green', 'yellow', 'blue'])

plt.scatter(beer['calories'], beer['alcohol'], c=color[beer['cluster']])

plt.scatter(centers.calories, centers.alcohol, linewidths=3, marker='+', s=300, c='black')

scatter_matrix(beer[["calories","sodium","alcohol","cost"]], s=100,alpha = 1 ,c=color[beer['cluster']],\
               figsize=(10, 10))  #alpha 代表不透明的意思
plt.suptitle("With 3 centroids initialized")

plt.show()

第四步：对数据进行标准化，再进行kmeans聚类

from sklearn.preprocessing import  StandardScaler
scaler = StandardScaler()
X_scaler = scaler.fit_transform(X)  #进行转换
new_X_scaler = pd.DataFrame(X_scaler, columns=["calories","sodium","alcohol","cost"])

km = KMeans(n_clusters=3).fit(X_scaler)

beer['scaler_cluster'] = km.labels_

beer.sort_values('scaler_cluster')

print(beer.groupby('scaler_cluster').mean())

scatter_matrix(new_X_scaler, alpha = 1 ,c=color[beer.scaler_cluster])

plt.show()

第五步：为了比较处理前后的效果，我们引入了轮廓系数 metrics.silhouette_score，发现未标准化的分类结果要好于标准化

from sklearn import metrics
score_scaled = metrics.silhouette_score(X,beer.scaler_cluster)
score = metrics.silhouette_score(X,beer.cluster)
print(score_scaled, score)

第六步： 我们使用轮廓系数(b(i)-a(i))/max(b(i), a(i)), b(i)一个点到自己蔟的距离,a(i)表示一个点到其他蔟的距离,来挑选蔟的参数n_clusters

scores = []
for i in range(2, 15):

    print(metrics.silhouette_score(X,KMeans(n_clusters=i).fit(X).labels_))  #X变量,KMeans(n_clusters=i).fit(X).labels_分类得到的标签

scores.append(metrics.silhouette_score(X,KMeans(n_clusters=i).fit(X).labels_)) plt.plot(list(range(2, 15)), scores) plt.xlabel('迭代次数') plt.ylabel('轮廓系数') plt.show()