二叉搜索树 思想 JAVA实现

二叉搜索树：一棵二叉搜索树是以一棵二叉树来组织的，这样一棵树可以使用链表的数据结构来表示（也可以采用数组来实现）。除了key和可能带有的其他数据外，每个节点还包含Left，Right，Parent，它们分别指节点的左孩子，右孩子，和父节点。

一个二叉搜索树总是满足 ：node.left.key<node.key<=node.right.key。

以下是一个用java实现的二叉搜索树，包含了查找最大值，最小值，查找某一节点，插入和删除操作。

接下来通过代码来分析二叉搜索树中的思想：在代码实现二叉搜索树中，大量采用了递归的思想，同样可以采用循环去递归来实现。

插入：自根节点起递归调用“寻找合适位置方法”，使二叉搜索树始终满足条件  node.left.key<node.key<=node.right.key。

查询：自根节点起递归调用“查找孩子的方法”。查找孩子的方法采用的思想是，判断node.key==key 返回，node.key>key 递归查找左子树，node.key<=key 递归查             找右子树。

查询最小值：递归查找左孩子，直到最后一个左孩子。

查询最大值：递归查找右孩子，直到最后一个右孩子。

遍历：

前序遍历：根的关键字输出在左右子树的关键字之前。根 左 右。

中序遍历：根的关键字输出在左右子树的关键字之间。左 根 右。

后序遍历：根的关键字输出在左右子树的关键字之后。左 右 根。

删除：删除一棵搜索树是比较麻烦的。共有以下4种情况

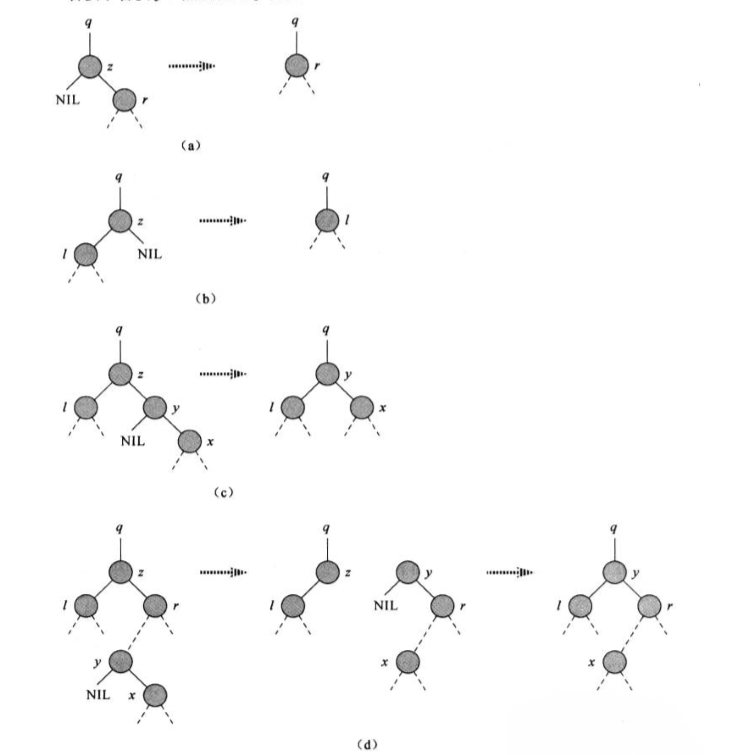
1.删除节点没有孩子，直接断开连接即可

2.a图：删除节点没有左孩子，将右孩子移至删除节点处

3.b图：删除节点没有右孩子，将左孩子移至删除节点处

4.c图：有左右孩子，右孩子 没有 左孩子，将右孩子移动至删除节点处，将左孩子的父节点连接值右孩子。

5.d图：有左右孩子，且右孩子也有左右孩子，则查找右孩子的最小节点，将最小节点移至删除节点处。

public class SearchTree {
                     //树的根节点
　　　　　　private Node Root = null;
                     //内部类，结点
　　　　　　private class Node{

　　　　　　　　　Node parent;//父节点
　　　　　　　　　Node Left;//左孩子
　　　　　　　　　Node Right;//右孩子
　　　　　　　　　int keyValue;//关键字

　　　　　　　　　public Node(Node parent,
　　　　　　　　　　　　　　　　Node Left,
　　　　　　　　　　　　　　　　Node Right,
　　　　　　　　　　　　　　　　int keyValue) {
　　　　　　　　　　this.parent = parent;
　　　　　　　　　　this.Left = Left;
　　　　　　　　　　this.Right = Right;
　　　　　　　　　　this.keyValue = keyValue;
　　　　　　　　　}
　　　　　　}

　　　　　　public void delete(int value) {
　　　　　　　　Node deleteNode = this.search(value);//查找删除节点
　　　　　　　　if(deleteNode.Left==null) {//没有左孩子
　　　　　　　　　　transplant(deleteNode, deleteNode.Right);
　　　　　　　　}else if(deleteNode.Right==null) {//没有右孩子
　　　　　　　　　　transplant(deleteNode, deleteNode.Left);
　　　　　　　　}else {//有左右孩子时
　　　　　　　　　　Node min = this.min(deleteNode.Right);//查找右孩子的最小节点
　　　　　　　　　　if(min.parent!=deleteNode) {
　　　　　　　　　　　　transplant(min, min.Right);
　　　　　　　　　　　　min.Right = deleteNode.Right;
　　　　　　　　　　　　min.Right.parent = min;
　　　　　　　　　　}
　　　　　　　　transplant(deleteNode, min);
　　　　　　　　min.Left = deleteNode.Left;
　　　　　　　　min.Left.parent = min;
　　　　　　　　}
　　　　　　}

//交换子树，将node2 移动至node1的位置。
　　　　　　private void transplant(Node node1,Node node2) {
　　　　　　　　if(node1.parent==null) {
　　　　　　　　　　this.Root = node2;
　　　　　　　　}else if(node1==node1.parent.Left) {
　　　　　　　　　　node1.parent.Left = node2;
　　　　　　　　}else {
　　　　　　　　　　node1.parent.Right= node2;
　　　　　　　　}
　　　　　　　　if(node2!=null) {
　　　　　　　　　　node2.parent = node1.parent;
　　　　　　　　}
　　　　　　}

//查找方法
　　　　　　public Node search(int value) {
　　　　　　　　return searchNode(this.Root,value);
　　　　　　}

　　　　　　private Node searchNode(Node node,int key) {
　　　　　　　　if(node==null || node.keyValue==key) {
　　　　　　　　　　return node;
　　　　　　　　}
　　　　　　　　if(node.keyValue>key) {
　　　　　　　　　　return this.searchNode(node.Left,key);
　　　　　　　　}else {
　　　　　　　　　　return this.searchNode(node.Right, key);
　　　　　　　　}
　　　　　　}

//插入方法
　　　　　　public void insert(int value) {
　　　　　　　　Node child = new Node(null, null, null, value);
　　　　　　　　findRightPlace(this.Root,child);
　　　　　　}

　　　　　　private void findRightPlace(Node currentRoot,Node insertNode) {
　　　　　　　　if(currentRoot!=null) {
　　　　　　　　　　　　if(currentRoot.keyValue>insertNode.keyValue) {
　　　　　　　　　　　　　　if(currentRoot.Left==null) {
　　　　　　　　　　　　　　　　currentRoot.Left = insertNode;
　　　　　　　　　　　　　　　　insertNode.parent = currentRoot;
　　　　　　　　　　　　　　}else {
　　　　　　　　　　　　　　　　findRightPlace(currentRoot.Left,insertNode);
　　　　　　　　　　　　       }
　　　　　　　　　　　　}else {
　　　　　　　　　　　　　　if(currentRoot.Right==null) {
　　　　　　　　　　　　　　　　currentRoot.Right = insertNode;
　　　　　　　　　　　　　　　　insertNode.parent = currentRoot;
　　　　　　　　　　　　　　}else {
　　　　　　　　　　　　　　　　findRightPlace(currentRoot.Right,insertNode);
　　　　　　　　　　　　　　}
　　　　　　　　　　　　}
　　　　　　　　}else {
　　　　　　　　　　　　this.Root = insertNode;
　　　　　　　　}
　　　　　　}

//查找最大
　　　　　　public int findMax() {
　　　　　　　　return max(this.Root)==null?-1:max(this.Root).keyValue;
　　　　　　}

　　　　　　private Node max(Node node) {
　　　　　　　　if(node!=null) {
　　　　　　　　　　if(node.Right!=null) {
　　　　　　　　　　　　return max(node.Right);
　　　　　　　　　　}else {
　　　　　　　　　　　　return node;
　　　　　　　　　　}
　　　　　　　　}else {
　　　　　　　　　　return null;
　　　　　　　　}
　　　　　　}

//查找最小
　　　　　　public int findMin() {
　　　　　　　　return min(this.Root)==null?-1:min(this.Root).keyValue;
　　　　　　}

　　　　　　private Node min(Node node) {
　　　　　　　　if(node!=null) {
　　　　　　　　　　if(node.Left!=null) {
　　　　　　　　　　　　return min(node.Left);
　　　　　　　　　　}else {
　　　　　　　　　　　　return node;
　　　　　　　　　　}
　　　　　　　　}else {
　　　　　　　　　　return null;
　　　　　　　　}
　　　　　　}

//后序遍历
　　　　　　public void after() {
　　　　　　　　afterShow(this.Root);
　　　　　　}

　　　　　　private void afterShow(Node node) {
　　　　　　　　if(node!=null) {
　　　　　　　　　　afterShow(node.Left);
　　　　　　　　　　afterShow(node.Right);
　　　　　　　　　　System.out.println(node.keyValue);
　　　　　　　　}
　　　　　　}

//中序遍历
　　　　　　public void mid() {
　　　　　　　　midShow(this.Root);
　　　　　　}

　　　　　　private void midShow(Node node) {
　　　　　　　　if(node!=null) {
　　　　　　　　　　midShow(node.Left);
　　　　　　　　　　System.out.println(node.keyValue);
　　　　　　　　　　midShow(node.Right);
　　　　　　　　}
　　　　　　}

//前序遍历
　　　　　　public void ahead() {
　　　　　　　　aheadShow(this.Root);
　　　　　　}

　　　　　　private void aheadShow(Node node) {
　　　　　　　　if(node!=null) {
　　　　　　　　　　System.out.println(node.keyValue);
　　　　　　　　　　aheadShow(node.Left);
　　　　　　　　　　aheadShow(node.Right);
　　　　　　　　}
}

参考资料 《算法导论》第三版