机器学习实战python3 决策树ID3

代码及数据：https://github.com/zle1992/MachineLearningInAction

决策树

优点:计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。
缺点:可能会产生过度匹配问题。
适用数据类型:数值型和标称型。

创建分支的伪代码函数createBranch()如下所示:
检测数据集中的每个子项是否属于同一分类:
if so return 类标签;
Else
　　寻找划分数据集的最好特征
　　划分数据集
　　创建分支节点
　　　　for 每个划分的子集
　　　　　　调用函数createBranch并增加返回结果到分支节点中
return 分支节点
上面的伪代码createBranch是一个递归函数，在倒数第二行直接调用了它自己。后面我们
寄把上面的伪代码转换为Python代码，这里我们需要进一步了解算法是如何划分数据集的。

1决策树构造

1.1创建数据

 def createDataSet():
     dataSet = [[1, 1, 'yes'],
                [1, 1, 'yes'],
                [1, 0, 'no'],
                [0, 1, 'no'],
                [0, 1, 'no']]
     labels = ['no surfacing','flippers']
     #change to discrete values
     return dataSet, labels

1.2信息增益

如果看不明白什么是信息增益(information gain)和墒( entropy )，请不要着急—创门自
诞生的那一天起，就注定会令世人十分费解。
嫡定义为信息的期望值，在明晰这个概念之前，我们必须知道信息的定义。如果待分类的事
务可能划分在多个分类之中，则符号xi，的信息定义为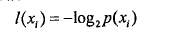

其中P(xi)是选择该分类的概率。
为了计算嫡，我们需要计算所有类别所有可能值包含的信息期望值，通过下面的公式得到:

其中n是分类的数目。

程序：计算给定数据集的香农熵

 def calcShannonEnt(dataSet):
     numEntries = len(dataSet) #Data 的大小N,N行
     labelCount = {}#字典存储 不同类别的个数
     for featVec in dataSet :
         currentLabel = featVec[-1] #每行的最后一个是类别
         if currentLabel not in labelCount.keys():
             labelCount[currentLabel] = 0
         labelCount[currentLabel] += 1  #原书缩进错误！！！
     shannonEnt = 0.0
     for key in labelCount:
         prob = float(labelCount[key])/numEntries
         shannonEnt -= prob *math.log(prob,2) #熵最后外面有个求和符号 ！！！
     return shannonEnt

1.3划分数据集

程序：划分数据集

 def splitDataSet(dataSet,axis,value):
     retDataSet = []
     for featVec in dataSet:
         if featVec[axis] == value:
             #去掉axis 这一列
             reducedFeatVec = featVec[:axis]
             reducedFeatVec.extend(featVec[axis+1: ])
             retDataSet.append(reducedFeatVec)
     return retDataSet  

划分数据集之后，使得划分后的纯度越小。选择信息增益最大的划分。

程序：选择最好的数据集划分方式

 def chooseBestFeatureTopSplit(dataSet):
     #列数 = len(dataset[0])
     #行数 = len(dataset)
     numFeatures = len(dataSet[0]) -1 #最后一列是标签
     baseEntropy = calcShannonEnt(dataSet) #所有数据的信息熵
     bestInfoGainn = 0.0
     bestFeature = -1
     for i in range(numFeatures):#遍历不同的属性
         featList = [example[i] for example in dataSet] #取出每一列
         uniqueVals = set(featList)
         newEntropy = 0.0
         for value in uniqueVals:#在第i个属性里，遍历第i个属性所有不同的属性值
             subDataSet = splitDataSet(dataSet,i,value) #划分数据
             prob = len(subDataSet)/float(len(dataSet))  #len([[]]) 行数
             newEntropy += prob *calcShannonEnt(subDataSet)
         infoGain = baseEntropy - newEntropy
         if(infoGain > bestInfoGainn):
             bestInfoGainn = infoGain
             bestFeature = i
     return bestFeature

1.4递归构建决策树

 def majorityCnt(classList):
     classCount ={}
     for vote in classList:
         if vote not in classCount.keys():
             classCount[vote] = 0
         classCount[vote] += 1

     classCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True) #与python2 不同！！！！！！python3 的字典items 就是迭代对象
     return classCount[0][0] #返回的是字典第一个元素的key 即 类别标签
 def createTree(dataSet,labels):
     #mytree 是一个字典，key 是属性值，val 是类别或者是另一个字典，
     #如果val 是类标签，则该子节点就是叶子节点
     #如果val是另一个数据字典，则该节点是一个判断节点
     classList = [example[-1] for example in dataSet]
     if classList.count(classList[0]) == len(classList): #类别完全相同，停止划分
         return classList[0]
     if len(dataSet[0])==1: #完全划分
         return majorityCnt(classList)
     bestFeat = chooseBestFeatureTopSplit(dataSet)
     bestFeatLabel = labels[bestFeat]
     myTree = {bestFeatLabel:{}}
     del(labels[bestFeat]) #
     featValues = [example[bestFeat] for example in dataSet] # 某属性的所有取值
     uniqueVals = set(featValues)
     for value in uniqueVals :
         subLabels = labels[:]
         myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
     return myTree

2在Python中使用Matplotlib注解绘制树形图

2.1使用文本注解绘制树节点

 #定义文本框跟箭头格式
 decisionNode = dict(boxstyle="sawtooth", fc="0.8")
 leafNode = dict(boxstyle="round4", fc="0.8")
 arrow_args = dict(arrowstyle="<-")
 def plotNode(nodeTxt, centerPt, parentPt, nodeType):
     createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords='axes fraction',
              xytext=centerPt, textcoords='axes fraction',
              va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )

2.2构造注解树

程序：获得叶子节点数与深度

 def getNumLeafs(myTree):
     numLeafs = 0
     firstStr = list(myTree)[0]#找到第一个节点
     secondDict = myTree[firstStr] #第二个节点
     for key in secondDict.keys(): #第二节点的字典的key
         if type(secondDict[key]).__name__=='dict':  #判断第二节点是否为字典
             numLeafs += getNumLeafs(secondDict[key]) #第二节点是字典 ，递归调用getNum
         else :numLeafs += 1 #第二节点不是字典，说明此节点是最后一个节点
     return numLeafs

 def getTreeDepth(myTree):
     maxDepth = 0
     firstStr = list(myTree)[0]#找到第一个节点
     secondDict = myTree[firstStr] #第二个节点
     for key in secondDict.keys(): #第二节点的字典的key
         if type(secondDict[key]).__name__=='dict':  #判断第二节点是否为字典
             thisDepth = 1 + getTreeDepth(secondDict[key]) #第二节点是字典 ，递归调用getNum
         else :thisDepth = 1 #第二节点不是字典，说明此节点是最后一个节点
     if thisDepth > maxDepth: maxDepth =thisDepth
     return maxDepth

程序：plotTree

 def plotMidText(cntrPt, parentPt, txtString):#在父子节点间填充文本信息
     xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
     yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
     createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)

 def plotTree(myTree, parentPt, nodeTxt):
     numLeafs = getNumLeafs(myTree)  #叶子节点个数
     depth = getTreeDepth(myTree)  #树的高度
     firstStr = list(myTree)[0] #！！！！！！！与py2不同
     cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff) #按照叶子结点个数划分x轴
     plotMidText(cntrPt,parentPt,nodeTxt)
     plotNode(firstStr,cntrPt,parentPt,decisionNode)
     secondDict = myTree[firstStr]
     plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD  #plotTree.yOff  全局变量
     for key in secondDict.keys():
         if type(secondDict[key]).__name__ =='dict':
             plotTree(secondDict[key],cntrPt,str(key))# 第二节点是字典，递归调用plotTree
         else:
             plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW #x方向计算结点坐标
             plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)#绘制子节点
             plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))#添加文本信息
     plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD #下次重新调用时恢复y
 def createPlot(inTree):
     fig = plt.figure(1, facecolor='white')
     fig.clf()
     axprops = dict(xticks=[], yticks=[])
     createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)  # no ticks
     # createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
     plotTree.totalW = float(getNumLeafs(inTree))
     plotTree.totalD = float(getTreeDepth(inTree))
     plotTree.xOff = -0.5 / plotTree.totalW
     plotTree.yOff = 1.0
     plotTree(inTree, (0.5, 1.0), '')
     plt.show()

程序：测试

 def retrieveTree(i):
     listOfTrees =[{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
                   {'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
                   ]
     return listOfTrees[i]
 if __name__ == '__main__':
     tree = retrieveTree(0)
     createPlot(tree)

3测试算法:使用决策树执行分类

使用决策树预测隐形眼镜类型

程序：使用决策树分类函数

 def classify(inputTree,featLabels,testVec):
     firstStr = list(inputTree.keys())[0]
     secondDict = inputTree[firstStr]
     featIndex = featLabels.index(firstStr) #将标签转化成索引
     for key in secondDict.keys():
         if testVec[featIndex] == key:
             if type(secondDict[key]).__name__=='dict':
                 classLabel = classify(secondDict[key],featLabels,testVec)
             else : classLabel = secondDict[key]#到达叶子节点，返回标签
     return classLabel

程序：使用pickle保存模型

 def storeTree(inputTree,filename):

     with open(filename,'wb') as f:
         pickle.dump(inputTree,f)

 def grabTree(filename):
     with open(filename,'rb') as f:
         t = pickle.load(f)
     return t

程序：主程序

 if __name__ == '__main__':
     #
     dataSet,labels = createDataSet()
     tree = createTree(dataSet,labels)
     storeTree(tree,"tree.model")
     tree = grabTree("tree.model")
     treePlotter.createPlot(tree)

     #读取txt文件，预测隐形眼镜的类型
     with open('lenses.txt') as f:
         lenses = [inst.strip().split('\t') for inst in f.readlines()]
     lensesLabels = ['age','prescript','astigmastic','tearRate']
     lensesTree = createTree(lenses,lensesLabels)
     treePlotter.createPlot(lensesTree)