Ural Sport Programming Championship 2015

Ural Sport Programming Championship 2015

A - The First Day at School

题目描述：给出课程安排，打印一个课程表。

solution

暴力模拟。

B - Maths

题目描述：给定一个数\(n\)，找出一个序列\(a_i\)满足\(\forall i \in [2, n], \sum_{j=1}^{j \leq i} a_j\) 有\(a_i\)个约数。

solution

暴力搜索，发现和不会超过\(2 \times 10^6\), 数字不会超过\(200\)，而且直接搜索即可很快求出答案。

时间复杂度：\(O(能过)\)

C - History

题目描述：求出从\(A\)年到\(B\)年中有\(1\)~\(12\)个黑色星期五的分别有多少年。

solution

显然有循环，模拟一下发现2800年左右有循环，因此只需要求出循环中每一年有多少个黑色星期五，然后求答案，求一下前缀和即可。

时间复杂度：\(O(2800 \times 12)\)

D - Chemistry

题目描述：给出\(n\)个杯子，每个杯子有一升的水，每次从一个杯子向另一个杯子倒水，使得后一个杯子的水变成原来的两倍，求出一种操作方案，使得最终有一个杯子有\(m\)升水，或无解。

solution

不会，本来想着好像二分那样弄就行，但发现会有副产品利用的情况，而且情况有些复杂。

E - 3D-modeling

题目描述：给定空间中的两条线段，问是否存在一条直线，使得一条线段绕直线转某个角度即可得到另一条直线，求出这条直线和对应的角度。

solution

不会

F - Physics

题目描述：有两个\(v(t)\)函数\(v_1, v_2\)，这两个函数都是折线函数，令\(h(t)=max(v_1(t), v_2(t)), g(t)=min(v_1(t), v_2(t))\)，给出\(h(t), g(t)\)的起点、终点、转折点，求出\(v_1(t), v_2(t)\)，使得两个函数所代表的位移相等。\(v_1, v_2\)重合点不超过\(30\)个。

solution

求出所有的重合点，假设开始时\(v_1=h, v_2=g\)，而只有遇到重合点的时候，\(v_1, v_2\)才有可能交换，即重合点将函数分成了若干段，每一段中的函数不能相交，因此可以分开前后两个部分进行搜索，然后判断是否存在一种方案使得合起来的位移等于总位移的一半。

注意：有可能\(h(t1) \neq g(t1)\)，但\(v_1(t1) = v_2(t1)\)

时间复杂度：\(O(2 \times 2^{15})\)

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=int(2e6)+100;
int T, n, m;
pair<int, int> h[maxn], g[maxn], tmp[maxn];
vector< pair<int, int> > v1, v2, cp;
map<LL, int> cnt;
LL sumh[maxn], sumg[maxn];
int block;
bool vis[maxn];
void read()
{
	scanf("%d", &T);
	scanf("%d", &n);
	for (int i=1; i<=n; ++i)
		scanf("%d%d" , &h[i].first, &h[i].second);
	scanf("%d", &m);
	for (int i=1; i<=m; ++i)
		scanf("%d%d", &g[i].first, &g[i].second);
}
void crosspoint()
{
	for (int i=1; i<=n; ++i) tmp[i]=h[i];
	int tmpn=n;
	n=1;
	for (int i=2; i<=tmpn; ++i)
		for (int j=tmp[i-1].first+1; j<=tmp[i].first; ++j)
			if (LL(j-tmp[i-1].first)*(tmp[i].second-tmp[i-1].second)%(tmp[i].first-tmp[i-1].first)==0)
				h[++n]=make_pair(j, LL(j-tmp[i-1].first)*(tmp[i].second-tmp[i-1].second)/(tmp[i].first-tmp[i-1].first)+tmp[i-1].second);
/*
	puts("h:");
	for (int i=1; i<=n; ++i) printf("%d %d\n", h[i].first, h[i].second);
	*/
	for (int i=1; i<=m; ++i) tmp[i]=g[i];
	int tmpm=m;
	m=1;
	for (int i=2; i<=tmpm; ++i)
		for (int j=tmp[i-1].first+1; j<=tmp[i].first; ++j)
			if (LL(j-tmp[i-1].first)*(tmp[i].second-tmp[i-1].second)%(tmp[i].first-tmp[i-1].first)==0)
				g[++m]=make_pair(j, LL(j-tmp[i-1].first)*(tmp[i].second-tmp[i-1].second)/(tmp[i].first-tmp[i-1].first)+tmp[i-1].second);
/*
	puts("g:");
	for (int i=1; i<=m; ++i) printf("%d %d\n", g[i].first, g[i].second);
	*/
	for (int i=1, j=1; i<=n && j<=m; ++i)
	{
		while (j<=m && g[j].first<h[i].first) ++j;
		if (j>m) continue;
		if (h[i].first==g[j].first && h[i].second==g[j].second)
			cp.push_back(h[i]);
	}
	if (h[n].second!=g[m].second) cp.push_back(h[n]);
/*
	puts("cp:");
	for (auto &i:cp) printf("%d %d\n", i.first, i.second);
	*/
}
void calc_sum()
{
	block=cp.size();
	LL s=0;
	for (int i=2, j=0; i<=n; ++i)
	{
		while (j<cp.size() && cp[j].first<h[i].first) ++j;
		s+=LL(h[i-1].second+h[i].second)*(h[i].first-h[i-1].first);
		if (j>=cp.size()) continue;
		if (cp[j].first==h[i].first) sumh[j]=s, s=0;
	}
	s=0;
	for (int i=2, j=0; i<=m; ++i)
	{
		while (j<cp.size() && cp[j].first<g[i].first) ++j;
		s+=LL(g[i-1].second+g[i].second)*(g[i].first-g[i-1].first);
		if (j>=cp.size()) continue;
		if (cp[j].first==g[i].first) sumg[j]=s, s=0;
	}
/*
	for (int i=0; i<block; ++i) printf("%lld ", sumh[i]);
	for (int i=0; i<block; ++i) printf("%lld ", sumg[i]);
	*/
}
inline LL det(pair<int, int> b, pair<int, int> c, pair<int, int> o)
{
	return (b.first-o.first)*(c.second-o.second)-(b.second-o.second)*(c.first-o.first);
}
void print(LL sett)
{
	for (int i=0, j=1, k=1; i<block; ++i)
	{
		if (sett>>i & 1)
		{
			while (j<=n && h[j].first<=cp[i].first) v1.push_back(h[j++]);
			while (k<=m && g[k].first<=cp[i].first) v2.push_back(g[k++]);
		}
		else
		{
			while (j<=n && h[j].first<=cp[i].first) v2.push_back(h[j++]);
			while (k<=m && g[k].first<=cp[i].first) v1.push_back(g[k++]);
		}
	}
	for (int i=0; i<v1.size(); ++i) vis[i]=true;
	for (int i=2; i<v1.size(); ++i)
		if (det(v1[i-2], v1[i-1], v1[i])==0) vis[i-1]=false;
	int ans=0;
	for (int i=0; i<v1.size(); ++i) ans+=vis[i];
	printf("%d\n", ans);
	for (int i=0; i<v1.size(); ++i)
		if (vis[i]) printf("%d %d\n", v1[i].first, v1[i].second);
	for (int i=0; i<v2.size(); ++i) vis[i]=true;
	for (int i=2; i<v2.size(); ++i)
		if (det(v2[i-2], v2[i-1], v2[i])==0) vis[i-1]=false;
	ans=0;
	for (int i=0; i<v2.size(); ++i) ans+=vis[i];
	printf("%d\n", ans);
	for (int i=0; i<v2.size(); ++i)
		if (vis[i]) printf("%d %d\n", v2[i].first, v2[i].second);
}
void solve()
{
	crosspoint();
	calc_sum();
	LL total=0;
	for (int i=0; i<block; ++i) total+=sumh[i]+sumg[i];
	total/=2;
	for (int i=0; i<1<<(block/2); ++i)
	{
		LL s=0;
		for (int j=0; j<block/2; ++j)
			if (i>>j & 1) s+=sumh[j];
			else s+=sumg[j];
		cnt[s]=i;
	}
	for (int i=0; i<1<<(block-block/2); ++i)
	{
		LL s=0;
		for (int j=0; j<block-block/2; ++j)
			if (i>>j & 1) s+=sumh[block/2+j];
			else s+=sumg[block/2+j];
		if (cnt.count(total-s))
		{
			print(cnt[total-s]|(i<<(block/2)));
			return;
		}
	}
}
int main()
{
	read();
	solve();
	return 0;
}

G - Physical Education

题目描述：给定一个数字\(n\)，将\(1\)到\(n\)重新排序：按各个位的数字的和从小到大排，相同的按预案数字从小到大排，问排序后的位置与原数字一样的数有多少个。

solution

先做一个数位\(dp\)，求出各个位的数字的和各有多少个，然后按这个进行分组，每一组最多只有可能有一个数字的位置与原数字的位置相同，这是因为在同一组中，相邻的数字的差事大于\(1\)的，因此不可能有两个数字的位置与原位置相同，如果有，那么这两个位置之间的数字的差必须都是\(1\)。

如果用新数列减去旧数列，则在同一组中，得到的数列是递增的，而我们要找的是是否存在一个等于零的位置，如果存在，则答案加一。这里可以用二分，每次二分用数位\(dp\)求出和与当前组的和一样的，小于等于某个数的数字有多少个，就可以判断是否存在。

时间复杂度：\(O(81 \times log(10^9) \times 9*10*81)\)

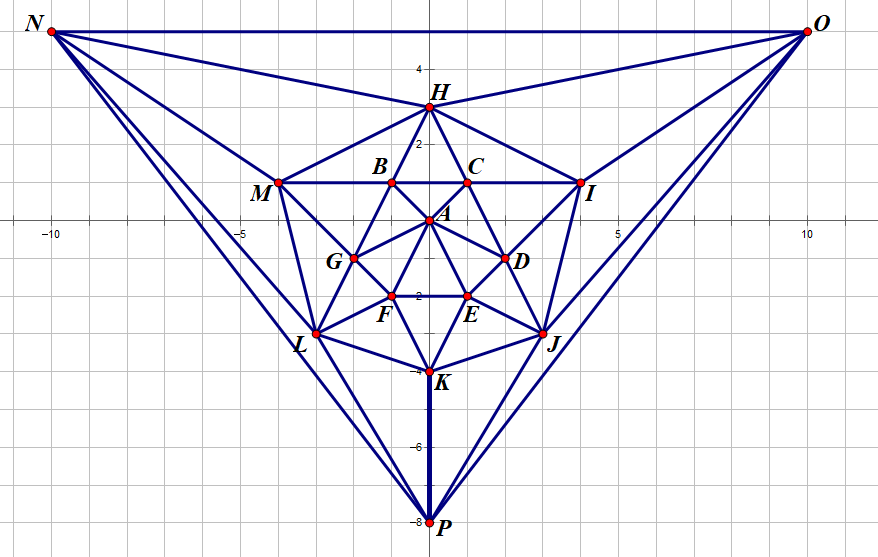
H - Biology

题目描述：在平面上找出\(16\)个点，然后构成一个平面图，使得该图中的简单环超过\(3\times10^5\)个。

solution

直接上图。

J - Urban Geography

题目描述：给出一个图，\(n\)个点，\(m\)条边，选择一些边，使得构成一颗生成树，而且选择的边的权值的最大值与最小值的差最小，输出方案。

solution

用\(LCT\)维护生成树，将边从小到大排序，然后逐条边添加进去，每次添加后把环里面的最小边删掉，更新答案。

时间复杂度：\(O(nlogn)\)

#include <bits/stdc++.h>
using namespace std;
const int maxn=int(5e4)+100;
const int inf=0x7fffffff;
struct node
{
	node *son[2], *fa;
	node *maxid;
	int value, num;
	bool reverse;
	node()
	{
		son[0]=son[1]=fa=NULL;
		maxid=NULL;
		value=inf;
		num=0;
		reverse=false;
	}
	void update()
	{
		maxid=this;
		if (son[0] && son[0]->maxid->value<maxid->value) maxid=son[0]->maxid;
		if (son[1] && son[1]->maxid->value<maxid->value) maxid=son[1]->maxid;
	}
	void down()
	{
		if (!reverse) return;
		if (son[0])
		{
			son[0]->reverse^=1;
			swap(son[0]->son[0], son[0]->son[1]);
		}
		if (son[1])
		{
			son[1]->reverse^=1;
			swap(son[1]->son[0], son[1]->son[1]);
		}
		reverse=false;
	}
	void rotate(int id)
	{
		node *y=fa;
		node *z=y->fa;
		fa=z;
		if (z && (z->son[0]==y || z->son[1]==y)) z->son[z->son[1]==y]=this;
		y->son[id]=son[id^1];
		if (son[id^1]) son[id^1]->fa=y;
		son[id^1]=y;
		y->fa=this;
		y->update();
		update();
	}
	void splay()
	{
		node *x=this;
		while (x->fa && (x->fa->son[0]==x || x->fa->son[1]==x))
		{
			node *y=x->fa;
			node *z=y->fa;
			if (z && (z->son[0]==y || z->son[1]==y)) z->down();
			y->down(); x->down();
			if (!z || (z->son[0]!=y && z->son[1]!=y)) x->rotate(y->son[1]==x);
			else
			{
				bool L=z->son[1]==y, R=y->son[1]==x;
				if (L^R) x->rotate(R), x->rotate(L);
				else y->rotate(L), x->rotate(R);
			}
		}
		x->down();
		x->update();
	}
	node *expose()
	{
		node *x=this;
		node *y=NULL;
		for (; x!=NULL; y=x, x=x->fa)
		{
			x->splay();
			x->son[1]=y;
			x->update();
		}
		return y;
	}
	node *askroot()
	{
		node *x=expose();
		while (x->son[0]) x=x->son[0];
		x->splay();
		return x;
	}
	void evert()
	{
		expose();
		splay();
		reverse=true;
		swap(son[0], son[1]);
	}
	void cut(node *x, node *y)
	{
		x->evert();
		y->expose();
		splay();
		x->fa=y->fa=NULL;
	}
	void clear()
	{
		son[0]=son[1]=fa=NULL;
		maxid=NULL;
		value=inf;
		num=0;
		reverse=false;
	}
};
struct LINK
{
	int x, y, dis;
	int num;
	bool operator < (const LINK b) const
	{
		return dis<b.dis;
	}
};
int n, m;
LINK edge[maxn];
node tree[maxn*2];
set< pair<int, int> > len;
bool vis[maxn];
void read()
{
	scanf("%d%d", &n, &m);
	for (int i=1; i<=m; ++i)
	{
		edge[i].num=i;
		scanf("%d%d%d", &edge[i].x, &edge[i].y, &edge[i].dis);
	}
}
node *askmin(node *x, node *y)
{
	x->evert();
	y->expose();
	x->splay();
	return x->maxid;
}
void connect(node *x, node *y, int v, int idx)
{
	node *z=tree+n+idx;
	z->value=v;
	z->num=idx;
	z->fa=x;
	y->evert();
	y->fa=z;
}
void solve()
{
	sort(edge+1, edge+1+m);
	int block=n;
	int minnum=inf;
	int ans;
	for (int i=1; i<=m; ++i)
	{
		node *u=tree+edge[i].x;
		node *v=tree+edge[i].y;
		len.insert(make_pair(edge[i].dis, i));
		if (u->askroot()!=v->askroot())
			connect(u, v, edge[i].dis, i), block--;
		else
		{
			node *x=askmin(u, v);
			len.erase(make_pair(x->value, x->num));
			x->cut(tree+edge[x->num].x, tree+edge[x->num].y);
			connect(u, v, edge[i].dis, i);
		}
		if (block!=1) continue;
		int tmp=len.begin()->first;
		if (edge[i].dis-tmp<minnum)
		{
			minnum=edge[i].dis-tmp;
			ans=i;
		}
	}
	for (int i=1; i<=n+m; ++i) (tree+i)->clear();
	for (int i=1; i<=ans; ++i)
	{
		node *u=tree+edge[i].x;
		node *v=tree+edge[i].y;
		vis[i]=true;
		if (u->askroot()!=v->askroot())
			connect(u, v, edge[i].dis, i), block--;
		else
		{
			node *x=askmin(u, v);
			x->cut(tree+edge[x->num].x, tree+edge[x->num].y);
			vis[x->num]=false;
			connect(u, v, edge[i].dis, i);
		}
	}
	for (int i=1; i<=m; ++i)
		if (vis[i]) printf("%d ", edge[i].num);
}
int main()
{
	read();
	solve();
	return 0;
}

K - Scholarship

solution

按题目说的做。