CF520E Pluses everywhere

题目大意

给定一个 n 位的十进制数，可以在数字之间加 k 个' + '，得到一个式子，求每种方案的这个式子的和

分析：

容易想到将式子的和转化为每个数字的贡献值之和。

设数组a为：a(n-1),a(n-2),...,a(0); 对于每一个位置，我们可以以其右面第一个放加号的位置为界，确定它的数位和贡献值。

对于a(k),循环0~k-1；再加上k的贡献值。 发现贡献值可以预处理。 f[y]表示i=0~y循环，10^i x C(n-i-2,m-1)的值。

公式就是：

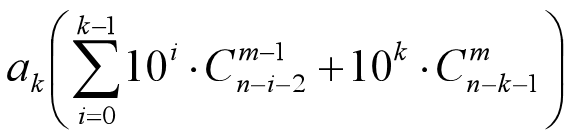
附代码：

#include<bits/stdc++.h>
#define ll long long
#define int long long
using namespace std;
const int N=1e5+;
const int mod=1e9+;
ll a[N],b[N];
int n,m;
char c;
ll fac[N],ifac[N];
ll f[N];
ll qm(int x,int y)
{
    ll base=x%mod;
    ll ans=;
    while(y)
    {
        if(y&) ans=(ans*base)%mod;
        base=(base*base)%mod;
        y>>=;
    }
    return ans%mod;
}
ll zu(int x,int y)
{
    if(x<||x<y||y<) return ;
    ll ret=fac[x]*ifac[y]%mod*ifac[x-y]%mod;
    return ret%mod;
}
ll ans=;
signed main()
{
    scanf("%lld%lld",&n,&m);
    for(int i=;i<=n;i++)
     {
        cin>>c;
        a[n-i]=c-'';
     }
    fac[]=;
    ifac[]=;
    for(int i=;i<=n;i++)
     fac[i]=(fac[i-]*i)%mod;
    ifac[n]=qm(fac[n],mod-)%mod;
    for(int i=n-;i>=;i--)
     ifac[i]=(ifac[i+]*(i+))%mod;
    f[]=zu(n-,m-);
    for(int i=;i<=n;i++)
     f[i]=(f[i-]+qm(,i)*zu(n-i-,m-)%mod)%mod;
    for(int i=;i<=n-;i++)
     if(i) ans=(ans+a[i]*f[i-]%mod+a[i]*qm(,i)%mod*zu(n-i-,m)%mod)%mod;
     else ans=(ans+a[i]*zu(n-,m)%mod)%mod;
    printf("%lld",ans%mod);
    return ;
}