UVA11987 Almost Union-Find

题目描述

PDF

输入输出格式

输入格式：

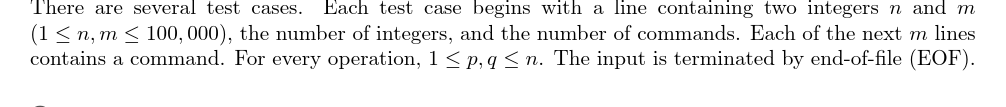
输出格式：

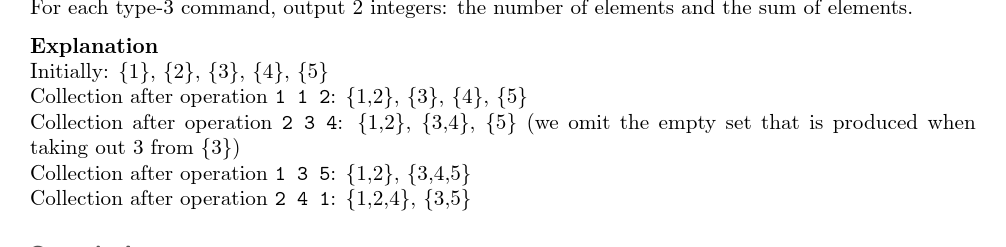
输入输出样例

输入样例#1：

5 7
1 1 2
2 3 4
1 3 5
3 4
2 4 1
3 4
3 3

输出样例#1：

3 12
3 7
2 8

Solution：

　　本题平衡树。

　　考试的时候想到的就是无旋treap了，正解貌似是并查集（我没想出来，太菜了）。

　　节点维护子树大小和子树和，开始时每个节点就是一棵treap，因为我们并不要保证有序，所以可以直接按中序遍历维护，合并分离就不需要考虑优先级了。

　　对于操作一，若不在同一棵树中，直接merge两棵树。

　　对于操作二，因为随机键值树高为$\log n$，所以直接暴力往上跳到$x$所在树的根，跳的同时求出$x$在该树中的排名，若$x,y$不在同一棵树中，按排名将$x$分离出来，与$y$所在树合并。

　　对于操作三，直接找到$x$所在树根输出子树大小和子树和就好了。

代码：

/*Code by 520 -- 10.24*/
#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define il inline
#define ll long long
#define RE register
#define For(i,a,b) for(RE int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(RE int (i)=(b);(i)>=(a);(i)--)
using namespace std;
const int N=;
int n,m,ch[N][],rnd[N],siz[N],date[N],cnt,fa[N],sum[N];

int gi(){
    int a=;char x=getchar();
    while(x<''||x>'') x=getchar();
    while(x>=''&&x<='') a=(a<<)+(a<<)+(x^),x=getchar();
    return a;
}

il void newnode(int v){
    ++cnt;
    ch[cnt][]=ch[cnt][]=,sum[cnt]=v;
    siz[cnt]=,date[cnt]=v,rnd[cnt]=rand(),fa[cnt]=;
}

il void up(int rt){
    if(ch[rt][]) fa[ch[rt][]]=rt;
    if(ch[rt][]) fa[ch[rt][]]=rt;
    siz[rt]=siz[ch[rt][]]+siz[ch[rt][]]+;
    sum[rt]=sum[ch[rt][]]+sum[ch[rt][]]+date[rt];
}

int merge(int x,int y){
    if(!x||!y) return x+y;
    if(rnd[x]<rnd[y]) {ch[x][]=merge(ch[x][],y),up(x);return x;}
    else {ch[y][]=merge(x,ch[y][]),up(y);return y;}
}

void split(int rt,int v,int &x,int &y){
    if(!rt) {x=y=;return;}
    if(siz[ch[rt][]]>=v) y=rt,split(ch[rt][],v,x,ch[y][]),up(y);
    else x=rt,split(ch[rt][],v-siz[ch[rt][]]-,ch[x][],y),up(x);
}

int find(int x,int &tot){
    if(!fa[x])return x;
    if(ch[fa[x]][]==x) tot+=siz[ch[fa[x]][]]+;
    return find(fa[x],tot);
}

int main(){
    srand(time());
    while(scanf("%d%d",&n,&m)!=EOF){
        cnt=; int opt,a,b,c,x,y,z;
        For(i,,n) newnode(i);
        while(m--){
            opt=gi(),a=gi();
            if(opt==){
                b=gi();
                a=find(a,x=),b=find(b,x=);
                if(a!=b) merge(a,b);
            }
            else if(opt==){ int k=siz[ch[a][]]+;
                b=gi();c=find(a,k),b=find(b,opt);
                if(c!=b){
                    x=y=z=;
                    split(c,k,x,y),split(x,k-,x,z),x=merge(x,y),b=merge(b,z);
                    fa[x]=,fa[b]=;
                }
            }
            else {
                a=find(a,x=);
                printf("%d %d\n",siz[a],sum[a]);
            }
        }
    }
    return ;
}