【LGR-048 五周年庆贺】洛谷6月月赛

Luogu的五周年庆典比赛，还是比较满意的。

题目清新不毒瘤，数据优质不卡常，解法自然，为出题人点赞。

前三题的难度都很低，T5个人感觉还好。但是最后那个splay+hash是什么神仙东西。

最后好像Rank50+，300pts里面没有时间的一个自带优越小常数

好了开始看题。

A: P4710「物理」平抛运动

这还是需要一定的物理基础的。在zitai dalao的教导下我终于还是听懂了。

首先我们直接用一下给的这张图：

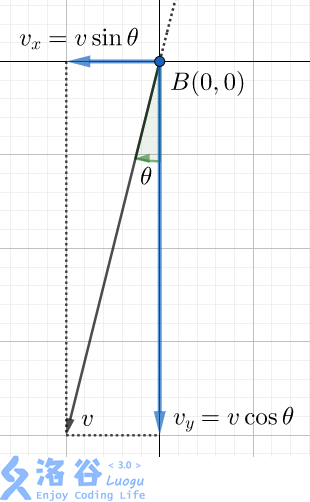
注意题目里的一句话：

首先，由于单位均为标准单位，所以所有结果均可以直接数字运算；视为质点意味着没有体积。

然后我们直接可以对于那个三角形的斜边和另一条直角边用三角函数表示出来：

其中横向的速度$v_x=v\ sin\ \theta $，纵向的速度$v_y=v\ cos\ \theta$

然后我们用物理中的一个加速度公式得到$v_y=g\cdot t$这就是公式我也没办法

所以我们可以先解出时间$t=\frac{v\ cos\ \theta}{g}$

然后小球的初始位置$(x,y)$就很好求了，其中：

$x=v_x\cdot t$（将速度分解后横向的就是匀速运动）
$y=\frac{gt^2}{2}$（这个初中生都知道吧）

然后就可以搞出来了

CODE

#include<cstdio>

#include<cmath>

using namespace std;

double v,a;

int main()

{

	scanf("%lf%lf",&v,&a); double t=v*cos(a)/10.0;

	printf("%.15lf %.15lf",v*sin(a)*t,t*t*5.0);

	return 0;

}

B: P4711 「化学」相对分子质量

由于感觉我很久没有写过大模拟了，然后就在比赛的时候义无反顾地开了这道题。

模拟题讲思路仅为个人菜鸡做法：

首先把有水合物的先搞出来单独处理掉（注意水之前的系数）
为了方便处理，我们对整个串预处理用一下，把所有的类似于"CO_{2}"的东西都变成"C_{1}O_{2}"
然后我们只需要找到所有的"_"然后对于前面的一整段一起处理即可，这样对于括号里面的方法就和外面一样了。
关于精度的处理我用了一个叫sprintf&&sscanf的奇技淫巧。当然都乘上$2$最后判断会更好。
对于那些化学分子式应该没有什么简单的方法，直接手动存map即可。

Upt：原来水合物是纯净物，害我期末考被科学老师骂了。把水合物当成混合物了

CODE

#include<string>

#include<map>

#include<iostream>

#include<cstdio>

#include<cstring>

using namespace std;

map <string,double> w;

string s;

int len,now,last,num=-1;

double v,ans;

char c[10];

inline void init(void)

{

	w["H"]=1; w["C"]=12; w["N"]=14; w["O"]=16;

	w["F"]=19; w["Na"]=23; w["Mg"]=24; w["Al"]=27;

	w["Si"]=28; w["P"]=31; w["S"]=32; w["Cl"]=35.5;

	w["K"]=39; w["Ca"]=40; w["Mn"]=55; w["Fe"]=56;

	w["Cu"]=64; w["Zn"]=65; w["Ag"]=108; w["I"]=127;

	w["Ba"]=137; w["Hf"]=178.5; w["Pt"]=195; w["Au"]=197; w["Hg"]=201;

}

inline double solve(int l,int r)

{

	string t=""; register int i;

	for (i=l;i<=r;++i)

	t+=s[i]; double ans=0;

	//cout<<t<<endl;

	if (t[0]!='(') return w[t];

	int last=1,len=t.size();

	for (i=0;i<len;++i)

	if (t[i]=='_')

	{

		string temp=""; if (i-1!=last) temp+=t[last],temp+=t[i-1]; else temp+=t[last];

		//cout<<temp<<endl;

		v=w[temp]; now=0; i+=2;

		while (i<len)

		{

			if (t[i]=='}') break;

			now=now*10+t[i]-'0'; ++i;

		}

		ans+=v*now; last=i+1;

	}

	return ans;

}

inline int find(int st)

{

	for (register int i=st;i<s.size();++i)

	if (s[i]==')') return i;

}

int main()

{

	ios::sync_with_stdio(false);

	register int i; cin>>s; len=s.size(); init();

	for (i=0;i<len;++i)

	if (s[i]=='~') { num=i; break; }

	if (num!=-1)

	{

		for (now=0,i=num+1;i<len;++i)

		if (s[i]!='H') now=now*10+s[i]-'0'; else break;

		ans+=now?now*18:18; s.erase(num,s.size()-num); len=s.size();

	}

	//cout<<s<<endl;

	for (i=0;i<s.size();++i)

	if (s[i]>='A'&&s[i]<='Z')

	{

		if (s[i+1]>='a'&&s[i+1]<='z')

		{

			if (s[i+2]!='_') s.insert(i+2,"_{1}");

		} else

		{

			if (s[i+1]!='_') s.insert(i+1,"_{1}");

		}

	} len=s.size();

	//cout<<s<<endl;

	for (i=0;i<len;++i)

	{

		//cout<<s[i]<<endl;

		if (s[i]=='(') i=find(i+1)+1;

		if (s[i]=='_')

		{

			v=solve(last,i-1); now=0; i+=2;

			while (i<len)

			{

				if (s[i]=='}') break;

				now=now*10+s[i]-'0'; ++i;

			}

			ans+=v*now; last=i+1;

		}

	}

	sprintf(c+1,"%.1lf",ans); int len=strlen(c+1);

	if (c[len]=='5')

	{

		for (i=1;i<=len;++i)

		putchar(c[i]);

	} else

	{

		for (i=1;i<=len-2;++i)

		putchar(c[i]);

	}

	return 0;

}

C: P4712 「生物」能量流动

一道非常简单的贪心题。

我们首先注意到既然要让能量的利用价值都最大，那么肯定转移的次数越少越好。

因此我们每次摄食都从当前允许的编号最小的生物开始摄食。

同时对于所有的点（除了人类）来说，刚刚摄取到足够的能量就可以了，因为剩下的都应该给人。

由于$r_i<r_{i+1}$，所以我们之前从之前的一路推过来即可。如果没有这个条件就要上线段树了。

CODE

// luogu-judger-enable-o2

#include<cstdio>

using namespace std;

const int N=1e5+5;

int last,n,r,x;

double a[N],b[N],ans;

inline char tc(void)

{

	static char fl[100000],*A=fl,*B=fl;

	return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;

}

inline void read(int &x)

{

	x=0; char ch=tc();

	while (ch<'0'||ch>'9') ch=tc();

	while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=tc();

}

int main()

{

	//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);

	register int i; read(n); read(x); a[0]=x;

	for (i=1;i<=n;++i)

	{

		read(x); b[i]=x; read(r);

		while (b[i])

		{

			if (last>r) return puts("-1"),0;

			if (a[last]*0.2>b[i]) a[last]-=b[i]*5,a[i]+=b[i],b[i]=0; else a[i]+=a[last]*0.2,b[i]-=a[last]*0.2,a[last]=0,++last;

		}

	}

	for (i=0;i<=n;++i)

	ans+=a[i]*0.2;

	return printf("%.8lf",ans),0;

}

F: P4714 「数学」约数个数和

一道非常猥琐的数学题，奇技淫巧爆棚。

我们先分析当$K=0$时，就是典型的约数个数公式。但我们进一步想一下这个公式是怎么来的：

我们将原来的数$N$拆分成$\prod {p_i}^{a_i}$。然后考虑对于每一个${p_i}^{a_i}$，都有$[0,a_i]$中选择方法，所以最后的个数就是$\prod a_i+1$

同样我们考虑对于$K=1$时，我们设现在的$a_i=2$。那么有那些可能？

就是$(0,0);(0,1);(0,1,2)$，那么方案数就变到$1+2+3$了。

或者我们可以更抽象化这个问题，令$n=a_i$,则有：

$a_1+a_2+......+a_{k+1}=n\ (a_i\ge 0)$

求合法的方案数。

我们左右都加上$k+1$得到：

$a_1+a_2+......+a_{k+1}=n+k+1(a_i>=1)$

然后就相当于在$n+k+1$个位置上选$k+1$个位置的问题了。这个的方案数就是$C_{n+k+1}^{k+1}$

这个鬼东西在$K\le 10^{18}$的情况下算不了，所以我们换一下变成$C_{n+k+1}^{n}$

最后要求的就是$\prod C_{a_i+k+1}^{a_i}$

由于$a_i<=60$，所以我们组合数部分直接上公式：

$C_m^n={\frac{m!}{n!\cdot(m-n)!}=\frac{\prod_{i=m-n+1}^m}{n!}}$

然后$n!$逆元处理。但由于这里$N\le 10^{18}$，所以要用到复杂度为神奇的$O(n^{\frac{1}{4}})$的Pollad-rho和大素数判定Miller-Rabin。这里不再多讲。

CODE

#include<cstdio>

#include<cstdlib>

#include<ctime>

#include<map>

using namespace std;

typedef long long LL;

const int mod=998244353;

map <LL,int> t;

map <LL,int> ::iterator it;

LL n,k,c=2333333,ans=1,inv[105];

inline LL quick_mul(LL n,LL m,LL mod)

{

    LL tot=0;

    while (m)

    {

        if (m&1) tot=(tot+n)%mod;

        n=(n+n)%mod; m>>=1;

    }

    return tot;

}

inline LL quick_pow(LL x,LL p,LL mod)

{

    LL tot=1;

    while (p)

    {

        if (p&1) tot=quick_mul(tot,x,mod);

        x=quick_mul(x,x,mod); p>>=1;

    }

    return tot;

}

inline LL C(LL n,LL m)

{

    LL tot=1;

    for (register int i=1;i<=m;++i)

    tot=tot*(n-i+1)%mod*inv[i]%mod;

    return tot;

}

inline LL gcd(LL n,LL m)

{

    return m?gcd(m,n%m):n;

}

inline bool Miller_Rabin(LL x)

{

    if (x==2) return 1;

    if (x<2||x&1==0) return 0;

    LL t=0,u=x-1;

    while (u&1==0) ++t,u>>=1;

    for (register int i=1;i<=20;++i)

    {

    	LL p=rand()%(x-1)+1,lst=quick_pow(p,u,x);

        for (register int j=1;j<=t;++j)

        {

            LL now=quick_mul(lst,lst,x);

            if (now==1&&lst!=1&&lst!=x-1) return 0; lst=now;

        }

        if (lst!=1) return 0;

    }

    return 1;

}

inline LL Pollard_rho(LL n,LL c)

{

    LL t=1,k=2,x=rand()%(n-1)+1,y=x;

    for (;;)

    {

        x=(quick_mul(x,x,n)+c)%n;

        LL p=gcd((y-x+n)%n,n);

        if (p!=1&&p!=n) return p;

        if (x==y) return n;

        if (++t==k) k<<=1,y=x;

    }

}

inline void find(LL n,LL c)

{

    if (n==1) return;

    if (Miller_Rabin(n)) { ++t[n]; return; }

    LL p=n,t=c;

    while (p>=n) p=Pollard_rho(n,c--);

    find(p,t); find(n/p,t);

}

int main()

{

    scanf("%lld%lld",&n,&k); srand(time(0)); find(n,c);

    for (register int i=1;i<=100;++i)

    inv[i]=quick_pow(i,mod-2,mod);

    for (it=t.begin();it!=t.end();++it)

    {

        ans=quick_mul(ans,C((k+1+it->second)%mod,it->second),mod);

    }

    printf("%lld",ans);

    return 0;

}

注意数可能会涉及两个$long\ long$级别的相乘但是模数也是$long\ long$的情况，所以我们还要写一个快速乘

Luogu第二道黑题get

剩下的两题由于我水平也有限，还是等坑吧。