Simple Question

一、你会在时间序列数据集上使用什么交叉验证技术？是用k倍？

　答：都不是。对于时间序列问题，k倍可能会很麻烦，因为第4年或第5年的一些模式有可能跟第3年的不同，而我们最终可能只是需要对过去几年的进行验证，这就不能用这种方法了。相反，我们可以采用如下所示的5倍正向链接策略：

　　fold 1 : training [1], test [2]

　　fold 2 : training [1 2], test [3]

　　fold 3 : training [1 2 3], test [4]

　　fold 4 : training [1 2 3 4], test [5]

　　fold 5 : training [1 2 3 4 5], test [6]

　　1，2，3，4，5，6代表的是年份

二、如何理解机器学习中的偏差与方差

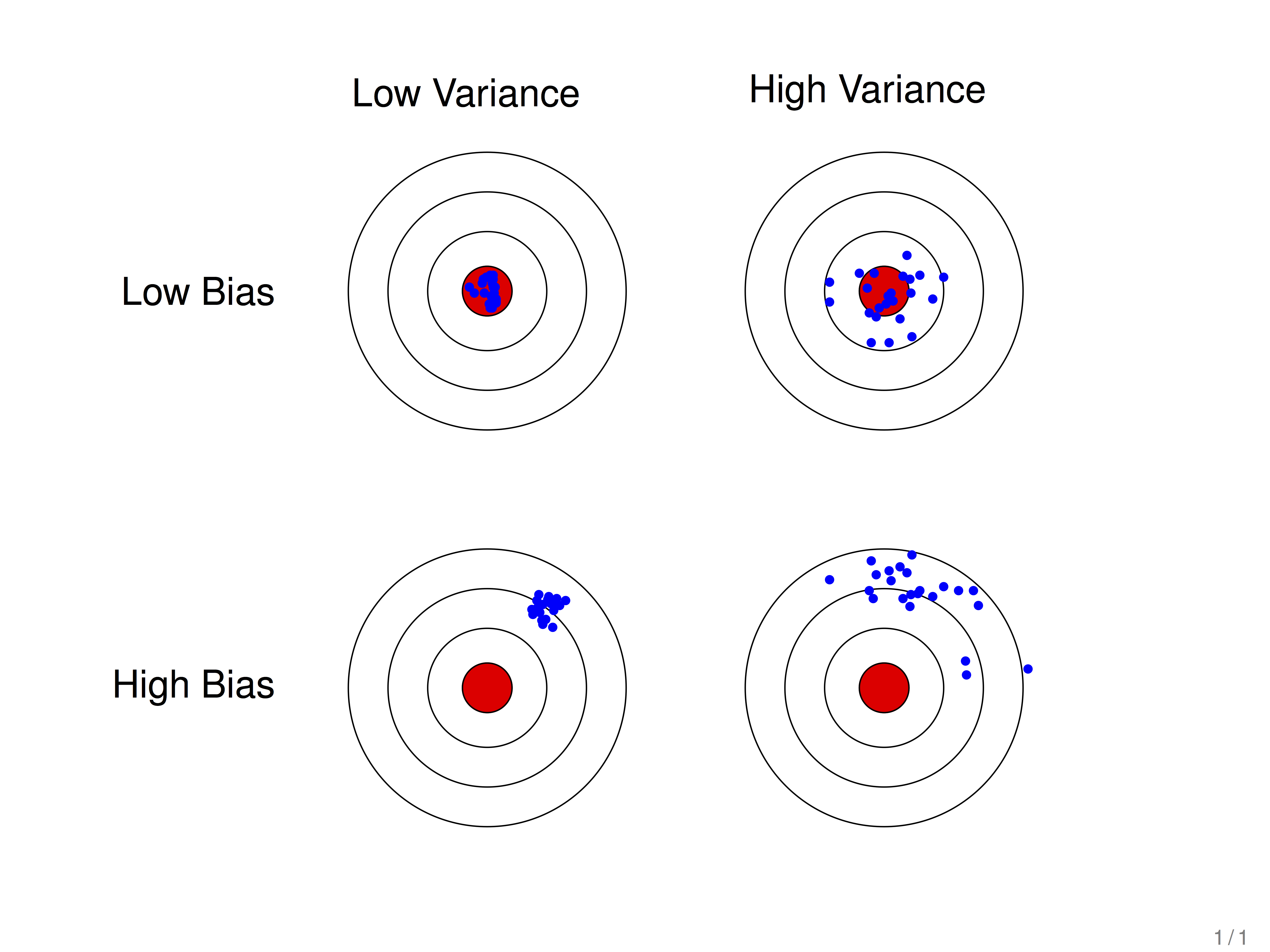
　学习算法的预测误差可以分解为三个部分: 偏差(bias), 方差(variance) 和噪声(noise). 在估计学习算法性能的过程中, 我们主要关注偏差与方差. 因为噪声属于不可约减的误差 (irreducible error).

　首先抛开机器学习的范畴, 从字面上来看待这两个词:

• 偏差

  这里的偏指的是偏离 , 那么它偏离了什么到导致了误差? 潜意识上, 当谈到这个词时, 我们可能会认为它是偏离了某个潜在的 “标准”, 而这里这个 “标准” 也就是真实情况 (ground truth). 在分类任务中, 这个 “标准” 就是真实标签 (label)

• 方差

  一个随机变量的方差描述的是它的离散程度, 也就是该随机变量在其期望值附近的波动程度

　

三、给你一个数据集，这个数据集有缺失值，且这些缺失值分布在离中值有1个标准偏差的范围内。百分之多少的数据不会受到影响？为什么？

　答：假设数据服从正态分布，学过大学高数的同学应该还记得，正态分布的一个背景知识点是，约95%的数据分布在均值周围2个标准差的范围内，约有68%的数据分布在均值周围1个标准差范围内，那么剩下的约32%的数据是不受影响的。因此，约有32%的数据将不受缺失值的影响

四、在k-means或kNN，我们是用欧氏距离来计算最近的邻居之间的距离。为什么不用曼哈顿距离？

　答：我们不用曼哈顿距离，因为它只计算水平或垂直距离，有维度的限制。另一方面，欧氏距离可用于任何空间的距离计算问题。因为，数据点可以存在于任何空间，欧氏距离是更可行的选择。例如：想象一下国际象棋棋盘，象或车所做的移动是由曼哈顿距离计算的，因为它们是在各自的水平和垂直方向做的运动。

五、花了几个小时后，现在你急于建一个高精度的模型。结果，你建了5 个GBM（Gradient Boosted Models），想着boosting算法会展现“魔力”。不幸的是，没有一个模型比基准模型表现得更好。最后，你决定将这些模型结合到一起。尽管众所周知，结合模型通常精度高，但你就很不幸运。你到底错在哪里？

　答：据我们所知，组合的学习模型是基于合并弱的学习模型来创造一个强大的学习模型的想法。但是，只有当各模型之间没有相关性的时候组合起来后才比较强大。由于我们已经试了5个GBM也没有提高精度，表明这些模型是相关的。具有相关性的模型的问题是，所有的模型提供相同的信息。例如：如果模型1把某一样本归类为1，模型2和模型3很有可能会做同样的分类，即使它的实际值应该是0，因此，只有弱相关的模型结合起来才会表现更好。

六、如何评价线性回归模型？

　我们知道，线性回归模型即找到一条直线，这条直线使得“误差平方和”最小（模型预测的值与实际值差值的平方），但是这可以作为评价模型的标准吗？先来看看下面一张表：

　从上表可以看出，同样的模型，只是样本数量不同，误差平方和却差好多，显然这个指标不能作为评价线性模型的标准，因为误差平方和随着样本量的增加而增加。

　R平方是最常用的评价线性回归模型好坏的指标

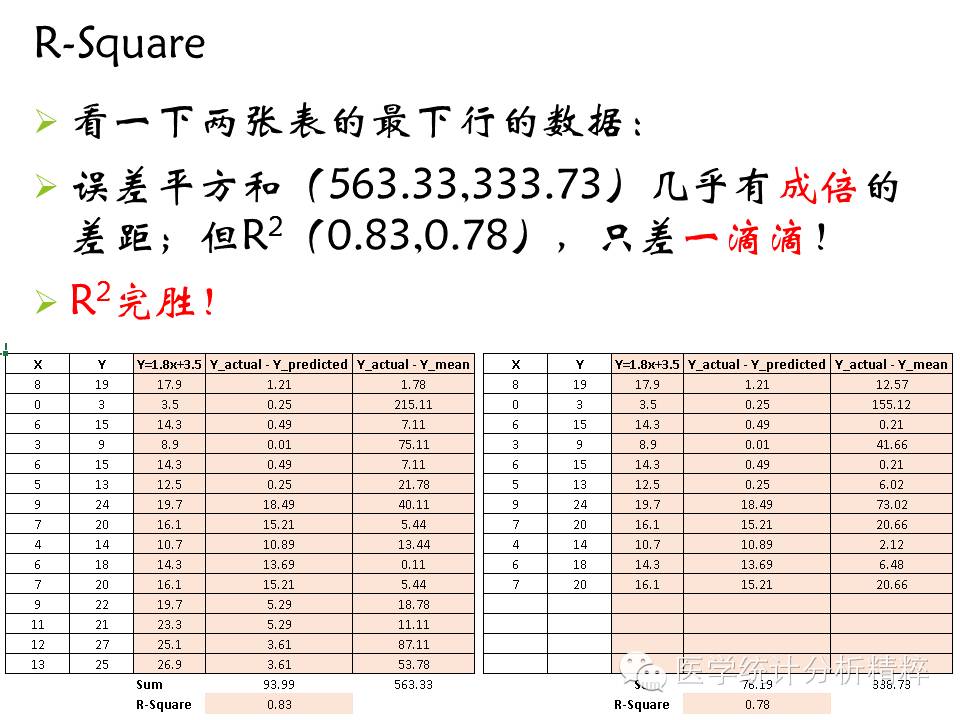
　但实际上，很少研究可以获得这么高的R方。社会学研究，R方超过0.1就算靠谱啦。医学研究，有个0.3，也是相当不错的！真若实现了R2 = 1.000，拒稿！

七、关于二分类问题的精确率和召回率

　评价分类器性能的指标一般是准确率，定义是：对于给定的测试集，分类器正确分类的样本数与总样本数之比。

　对于二分类问题常用的指标是精确率和召回率：

　　TP-将正类预测为正类数

　　FN-将正类预测为负类数

　　FP-将负类预测为正类数

　　TN-将负类预测为负类数

　精确率：P = TP/(TP + FP)

　召回率：R = TP/(TP + FN)

　此外，还有F1值，是精确率和召回率的调和均值，即：2/F1 = 1/P + 1/R

八、对于树形结构为什么不需要归一化？

　数值缩放，不影响分裂点位置。因为第一步都是按照特征值进行排序的，排序的顺序不变，那么所属的分支以及分裂点就不会有不同。对于线性模型，比如说LR，我有两个特征，一个是(0,1)的，一个是(0,10000)的，这样运用梯度下降时候，损失等高线是一个椭圆的形状，这样我想迭代到最优点，就需要很多次迭代，但是如果进行了归一化，那么等高线就是圆形的，那么SGD就会往原点迭代，需要的迭代次数较少。
　另外，注意树模型是不能进行梯度下降的，因为树模型是阶跃的，阶跃点是不可导的，并且求导没意义，所以树模型（回归树）寻找最优点是通过寻找最优分裂点完成的。