HDU 3594.Cactus 仙人掌图

Cactus

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2206    Accepted Submission(s): 1039

Problem Description

1. It is a Strongly Connected graph.
2. Each edge of the graph belongs to a circle and only belongs to one circle.
We call this graph as CACTUS.

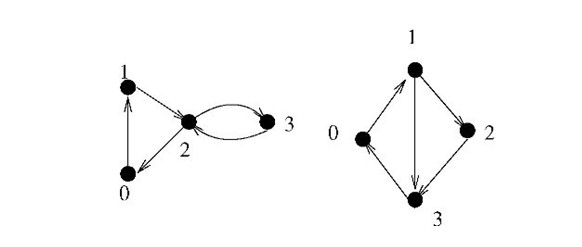
There is an example as the figure above. The left one is a cactus, but the right one isn’t. Because the edge (0, 1) in the right graph belongs to two circles as (0, 1, 3) and (0, 1, 2, 3).

 

Input

The input consists of several test cases. The first line contains an integer T (1<=T<=10), representing the number of test cases.
For each case, the first line contains a integer n (1<=n<=20000), representing the number of points.
The following lines, each line has two numbers a and b, representing a single-way edge (a->b). Each case ends with (0 0).
Notice: The total number of edges does not exceed 50000.

 

Output

For each case, output a line contains “YES” or “NO”, representing whether this graph is a cactus or not.

 

Sample Input

2

4

0 1

1 2

2 0

2 3

3 2

0 0

4

0 1

1 2

2 3

3 0

1 3

0 0

 

Sample Output

YES

NO

 

Author

alpc91

 

Source

2010 ACM-ICPC Multi-University Training Contest（16）——Host by NUDT

 

Recommend

zhengfeng   |   We have carefully selected several similar problems for you:  3593 3600 3599 3598 3595 

 

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3594

题意：判断是否是仙人掌图。

仙人掌图分析

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<bitset>
using namespace std;
#define PI acos(-1.0)
#define eps 1e-8
typedef long long ll;
typedef pair<int,int> P;
const int N=1e5+,M=1e5+;
const int inf=0x3f3f3f3f;
const ll INF=1e18+,mod=1e9+;
struct edge
{
    int from,to;
    int next;
};
edge es[M];
int cut,head[N];
int scc_cut=,dfs_clock=;
int pre[N],low[N];
int vis[N],fa[N];
stack<int>s;
void init()
{
    cut=;
    memset(head,-,sizeof(head));
}
void addedge(int u,int v)
{
    cut++;
    es[cut].from=u,es[cut].to=v;
    es[cut].next=head[u];
    head[u]=cut;
}
bool findfa(int u,int pa)
{
    while(fa[u]!=pa)
    {
        if(++vis[u]>) return false;
        u=fa[u];
    }
    return true;
}
bool dfs(int u)
{
    pre[u]=low[u]=++dfs_clock;
    s.push(u);
    for(int i=head[u]; i!=-; i=es[i].next)
    {

        int v=es[i].to;
        if(!pre[v])
        {
            fa[v]=u;
            if(!dfs(v)) return false;
            low[u]=min(low[u],low[v]);
        }
        else
        {
            low[u]=min(low[u],pre[v]);
            if(!findfa(u,v)) return false;
        }
    }
    if(pre[u]==low[u])
    {
        if(++scc_cut>) return false;
        while(!s.empty())
        {
            int v=s.top();
            s.pop();
            if(v==u) break;
        }
    }
    return true;
}
bool solve(int n)
{
    scc_cut=dfs_clock=;
    memset(pre,,sizeof(pre));
    memset(low,,sizeof(low));
    memset(vis,,sizeof(vis));
    for(int i=; i<n; i++)
        if(!pre[i]&&!dfs(i)) return false;
    return true;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        init();
        int n,u,v;
        scanf("%d",&n);
        while(scanf("%d%d",&u,&v)&&!(u==&&v==))
            addedge(u,v);
        if(solve(n)) puts("YES");
        else puts("NO");
    }
    return ;
}

强联通分量 仙人掌图

代码：