网络流棋盘模型 | P3355 骑士共存问题 P4304 [TJOI2013]攻击装置

题面（骑士共存问题）

在一个 \(n \times n\) 个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入。

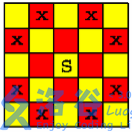
对于给定的 \(n \times n\) 个方格的国际象棋棋盘和 \(m\) 个障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击。

对于全部的测试点，保证 \(1 \leq n \leq 200\)，\(0 \leq m \lt n^2\)。

思路

二分图的最大独立集。

先对这个棋盘进行黑白染色，然后发现，同颜色的格子的马永远无法互相攻击。

首先，先创立源点 \(s\)，汇点 \(t\)。

然后对于白点 \((i,j)\)，连边 \((s,(i,j),1)\)。对于黑点 \((k,l)\)，连边 \(((k,l),t,1)\)，对于可以互相攻击的点 \((a,b),(c,d)\)，连边 \(((a,b),(c,d),+\infty)\)。

然后求最大独立集。

代码

P3355 骑士共存问题

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n,m,s,t;

struct edge{
	int from,to,val;
}e[2000001];int head[2000001],cur[2000001],siz=1;
void addedge(int x,int y,int z){
	e[++siz].to=y,e[siz].val=z;
	e[siz].from=head[x],head[x]=siz;
}
void add(int x,int y,int z){
	addedge(x,y,z);
	addedge(y,x,0);
}

int gap[2000001];
bool bfs(){
	memset(gap,0,sizeof(gap));
	fill(gap+1,gap+1+n,0);
	queue<int> q;
	q.push(s);
	gap[s]=1;
	while(!q.empty()){
		int now=q.front();
		q.pop();
		for(int i=head[now];i;i=e[i].from){
			int u=e[i].to;
			if(e[i].val&&!gap[u]){
				gap[u]=gap[now]+1;
				q.push(u);
			}
		}
	}
	return (gap[t]);
}
int dfs(int now,int val){
	if(now==t) return val;
	for(int &i=cur[now];i;i=e[i].from){
		int u=e[i].to;
		if(e[i].val&&gap[now]+1==gap[u]){
			int F=dfs(u,min(e[i].val,val));
			if(F){
				e[i].val-=F;
				e[i^1].val+=F;
				return F;
			}
		}
	}
	return 0;
}
int dinic(){
	int ret=0;
	while(bfs()){
		copy(head,head+1+n,cur);
		int F=0;
		while(F=dfs(s,10000000000000)){
			ret+=F;
		}
	}
	return ret;
}

int knight[100000][1000];

int mk(int x,int y){
	x--;
	return (x*n+y);
}

int delta[][2]={{1,2},{1,-2},{-1,2},{-1,-2},{2,1},{2,-1},{-2,1},{-2,-1}};

bool valid(int x){
	return (x>=1)&&(x<=n);
}

signed main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int x,y;
		cin>>x>>y;
		knight[x][y]=1;
	}
	s=0,t=n*n+1;

	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if((i+j)%2&&!knight[i][j]){
				add(s,mk(i,j),1);
			}
			if(!((i+j)%2)&&!knight[i][j]){
				add(mk(i,j),t,1);
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if((i+j)%2==0){
				continue;
			}
			for(int k=0;k<8;k++){
				int tx=i+delta[k][0];
				int ty=j+delta[k][1];
				if(valid(tx)&&valid(ty)){
					if(!knight[tx][ty]){
						add(mk(i,j),mk(tx,ty),INT_MAX);
					}
				}
			}
		}
	}
	n=n*n;
	cout<<n-m-dinic()<<'\n';
	return 0;
}

P4304 [TJOI2013]攻击装置

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n,m,s,t;

struct edge{
	int from,to,val;
}e[200001];int head[200001],cur[200001],siz=1;
void addedge(int x,int y,int z){
	e[++siz].to=y,e[siz].val=z;
	e[siz].from=head[x],head[x]=siz;
}
void add(int x,int y,int z){
	addedge(x,y,z);
	addedge(y,x,0);
}

int gap[200001];
bool bfs(){
	memset(gap,0,sizeof(gap));
	fill(gap+1,gap+1+n,0);
	queue<int> q;
	q.push(s);
	gap[s]=1;
	while(!q.empty()){
		int now=q.front();
		q.pop();
		for(int i=head[now];i;i=e[i].from){
			int u=e[i].to;
			if(e[i].val&&!gap[u]){
				gap[u]=gap[now]+1;
				q.push(u);
			}
		}
	}
	return (gap[t]);
}
int dfs(int now,int val){
	if(now==t) return val;
	for(int &i=cur[now];i;i=e[i].from){
		int u=e[i].to;
		if(e[i].val&&gap[now]+1==gap[u]){
			int F=dfs(u,min(e[i].val,val));
			if(F){
				e[i].val-=F;
				e[i^1].val+=F;
				return F;
			}
		}
	}
	return 0;
}
int dinic(){
	int ret=0;
	while(bfs()){
		copy(head,head+1+n,cur);
		int F=0;
		while(F=dfs(s,10000000000000)){
			ret+=F;
		}
	}
	return ret;
}

int knight[10000][1000];

int mk(int x,int y){
	x--;
	return (x*n+y);
}

int delta[][2]={{1,2},{1,-2},{-1,2},{-1,-2},{2,1},{2,-1},{-2,1},{-2,-1}};

bool valid(int x){
	return (x>=1)&&(x<=n);
}

int gc(){
	char ch;
	do{
		ch=getchar();
	}while(!isdigit(ch));
	return ch-'0';
}

signed main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			knight[i][j]=gc();
			m+=knight[i][j];
		}
	}
	s=0,t=n*n+1;

	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if((i+j)%2&&!knight[i][j]){
				add(s,mk(i,j),1);
			}
			if(!((i+j)%2)&&!knight[i][j]){
				add(mk(i,j),t,1);
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if((i+j)%2==0){
				continue;
			}
			for(int k=0;k<8;k++){
				int tx=i+delta[k][0];
				int ty=j+delta[k][1];
				if(valid(tx)&&valid(ty)){
					if(!knight[tx][ty]){
						add(mk(i,j),mk(tx,ty),INT_MAX);
					}
				}
			}
		}
	}
	n=n*n;
	cout<<n-m-dinic()<<'\n';
	return 0;
}

习题：P5030 长脖子鹿放置

题面

众周所知，在西洋棋中，我们有城堡、骑士、皇后、主教和长脖子鹿。

如图所示，西洋棋的“长脖子鹿”，类似于中国象棋的马，但按照“目”字攻击，且没有中国象棋“别马腿”的规则。（因为长脖子鹿没有马腿）

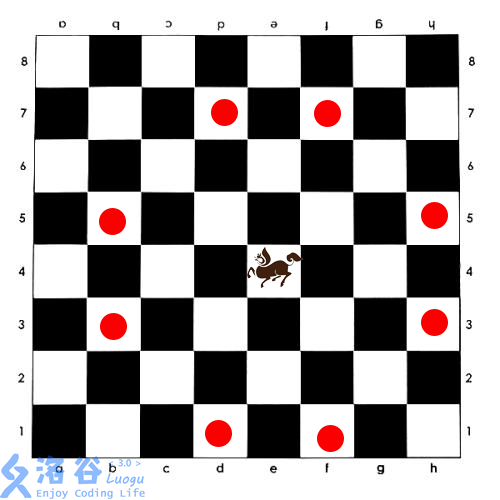
给定一个\(N * M\),的棋盘，有 \(k\) 个格子禁止放棋子。问棋盘上最多能放多少个不能互相攻击的长脖子鹿。

对于\(100\)%的数据，\(1 ≤ N,M ≤ 200\)

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n,m,s,t;

struct edge{
	int from,to,val;
}e[2000001];int head[2000001],cur[2000001],siz=1;
void addedge(int x,int y,int z){
	e[++siz].to=y,e[siz].val=z;
	e[siz].from=head[x],head[x]=siz;
}
void add(int x,int y,int z){
	addedge(x,y,z);
	addedge(y,x,0);
}

int gap[2000001];
bool bfs(){
	memset(gap,0,sizeof(gap));
	fill(gap+1,gap+1+n,0);
	queue<int> q;
	q.push(s);
	gap[s]=1;
	while(!q.empty()){
		int now=q.front();
		q.pop();
		for(int i=head[now];i;i=e[i].from){
			int u=e[i].to;
			if(e[i].val&&!gap[u]){
				gap[u]=gap[now]+1;
				q.push(u);
			}
		}
	}
	return (gap[t]);
}
int dfs(int now,int val){
	if(now==t) return val;
	for(int &i=cur[now];i;i=e[i].from){
		int u=e[i].to;
		if(e[i].val&&gap[now]+1==gap[u]){
			int F=dfs(u,min(e[i].val,val));
			if(F){
				e[i].val-=F;
				e[i^1].val+=F;
				return F;
			}
		}
	}
	return 0;
}
int dinic(){
	int ret=0;
	while(bfs()){
		copy(head,head+1+n,cur);
		int F=0;
		while(F=dfs(s,10000000000000)){
			ret+=F;
		}
	}
	return ret;
}

int knight[100000][1000];

int mk(int x,int y){
	x--;
	return (x*m+y);
}

int delta[][2]={{1,3},{1,-3},{-1,3},{-1,-3},{3,1},{3,-1},{-3,1},{-3,-1}};

bool valid(int x){
	return (x>=1)&&(x<=n);
}
bool validy(int x){
	return (x>=1)&&(x<=m);
}

int kkk,k;

signed main(){
	cin>>n>>m>>kkk;
	for(int i=1;i<=kkk;i++){
		int x,y;
		cin>>x>>y;
		if(!knight[x][y]){
			k++;
		}
		knight[x][y]=1;
	}
	s=0,t=n*m+1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if((i)%2){
				add(s,mk(i,j),1);
			}
			if(!((i)%2)){
				add(mk(i,j),t,1);
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(knight[i][j]){
				continue;
			}
			if((i)%2==0){
				continue;
			}
			for(int k=0;k<8;k++){
				int tx=i+delta[k][0];
				int ty=j+delta[k][1];
				if(valid(tx)&&validy(ty)){
					if(!knight[tx][ty]){
						add(mk(i,j),mk(tx,ty),1);
					}
				}
			}
		}
	}
	n=n*m;
	cout<<n-k-dinic()<<'\n';
	return 0;
}