c++代码实现中时间复杂度的不断优化

先来介绍一下时间复杂度：

同一问题可用不同算法解决，而一个算法的质量优劣将影响到算法乃至程序的效率。算法分析的目的在于选择合适算法和改进算法。

计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，它考察当输入值大小趋近无穷时的情况。

---

时间复杂度的优化通常在暴力枚举中尤为重要，或许O(n*n)会得零分但是O(n*logn)可以得满分，所以在编写程序过程中我们要优先考虑时间较短的算法（洛谷里最绝望的就是看到TLE，这意味着代码要重新编写）。总之有快方法用上绝对没问题，除非NOIP时间不够可以快速写一段骗（拿）一些分数。

---

---

下面以洛谷P2241 统计方形（数据加强版）为例讲解一下具体如何不断优化程序的时间复杂度：

例10.1 (洛谷 P2241， NOIP1997 普及组 加强)

有一个 n×m(n, m ≤ 5000) 的棋盘，求其方格包含多少个(四边平 行于坐标轴的)正方形和长方形。

本题中， 长方形中不包括正方形。

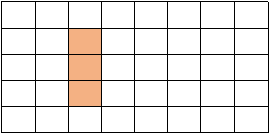
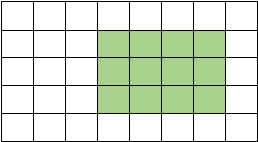
样例解释： 如图，正方形一共 8 个，长方形 10 个 正方形中，边长为 1 的 6 个，边长为 2 的 2 个；

　　　　　长方形中， 1 ×2 的 4 个， 1 ×3 的 2 个， 2 × 1 的 3 个， 2 ×3 的 1个。

---

思路1：用四重循环，直接枚举 4 个参数，即两横边两竖边：

通过左上角和右下角的顶点进行枚举，如果长度相等就是正方形，否则就是长方形。

所以，这样可以保证不重复地遍历所有的方形。

根据循环的范围可知，我们也没有遗漏任何的方形。

时间复杂度O(n2 m2 ) ……似乎有点慢。

但是至少， 答案正确了。

 1 //枚举左上、右下顶点 时间复杂度O(n^2*m^2)
 2 #include<bits/stdc++.h>
 3 using namespace std;
 4 typedef long long LL; //LL是已经定义好的long long
 5 int main(){
 6     int n,m;
 7     LL squ=0,rec=0;//squ统计正方形个数,rec统计长方形个数
 8     cin>>n>>m;
 9     for(int x1=0;x1<n;x1++)
10     for(int y1=0;y1<m;y1++)
11     for(int x2=x1+1;x2<=n;x2++)
12     for(int y2=y1+1;y2<=m;y2++)    //四层循环不TLE才怪
13         if (x2-x1 == y2-y1)squ++;
14         else rec++;
15     cout<<squ<<" "<<rec<<endl;
16     return 0;
17 }

                

为什么是 x2 从 x1+1 开始， y2 从 y1+1 开始枚举？

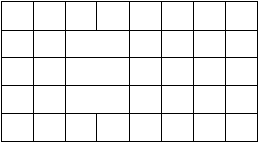
• 如果 x1 > x2， 那么 x1 就不再是左侧了， x2 才是左侧 (左图)

• 如果 x1 = x2， 那么无法构成长方形， 退化为一根线段 (中图)（就是那根消失的线段）

• 只有 x1 < x2， 才能正常构成长方形(右图)。

y1 、y2 同理

---

---

思路 2： 以下左图中的点 (3, 4)为例(左下角为原点)。

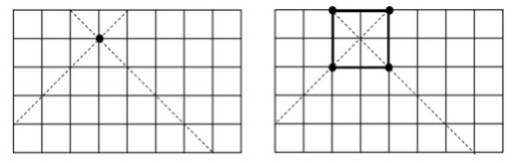
位于同一对角线 (图中虚线)上所有点均可构成正方形。

除自身所在行列外，所有其它点均可与其构成长方形；故直接得 长方形数为 nm – 正方形数。

从右图可以看出， 每一个长/正方形均被其 4 个顶点各计算一次。 因此，最终答案需要除以 4。

斜线上的格点个数为多少呢？

若顶点在长方形顶点，格点个数为长方形的短边长，即 min(n,m)。

否则，以顶点为界分为4份 。

每份都这样计算，得到正方形个数： min x, y + min n − x, y + min x, m − y + min(n − x, m − y)

因此， 枚举(x, y)后，可在 O(1) 时间内计算答案，求和。 总时间复杂度 O(nm)，直接优化掉一个 O(nm)

 1 //枚举一个点构成的所有矩形，统计结果除4 时间复杂度O(n*m)
 2 #include<bits/stdc++.h>
 3 using namespace std;
 4 typedef long long LL; //LL是已经定义好的long long
 5 int main(){
 6     int n,m;
 7     LL squ=0,rec=0;
 8     cin>>n>>m;
 9     for(int x=0;x<=n;x++)
10     for(int y=0;y<=m;y++){
11         LL tmp=min(x,y)+min(n-x,y)+min(x,m-y)+min(n-x,m-y);//对角线的正方形枚举方式
12         squ+=tmp;
13         rec+=n*m-tmp;
14     }
15     cout<<squ/4<<" "<<rec/4<<endl;//四个顶点算了四次，所以要除4输出
16     return 0;
17 }

---

---

还能不能更快呢？

思路 3：每一个长方形重复了4次。能否不重复呢？

结合思路 1可知， 只需考虑右上角为 (x, y) 的情况，因此计算斜线 上的顶点时， 只需要向左下角一个方向拓展！

(先算 4 个方向， 再除以 4，可谓是画蛇添足啊…… )

 1 //枚举右下角顶点 时间复杂度O(n*m)
 2 #include<bits/stdc++.h>
 3 using namespace std;
 4 typedef long long LL;
 5 int main(){
 6     int n,m;
 7     LL squ=0,rec=0;
 8     cin>>n>>m;
 9     for(int x=0;x<=n;x++)
10         for(int y=0;y<=m;y++){
11             LL tmp=min(x,y);
12             squ+=tmp;
13             rec+=x*y-tmp;
14         }
15     cout<<squ<<" "<<rec<<endl;
16     return 0;
17 }

当然，这里选择固定其它角也是等价的，但是固定右上角最简单。

注意：这里的原点是在左下角， 列是 x，行是 y。

如果选择左上角 作为原点， 那么枚举的就是长方形右下角。

---

---

思路4：枚举边长 (a, b)。题目变为在 n × m 的长方形中能放置多少 个 a×b 的方形。

注意 a 、b 有序， a×b 和 b×a 不等价。

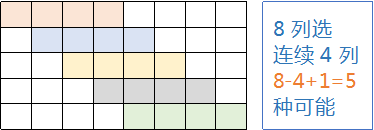
• n 列中选连续 a 列：[1,a],[2,a+1], … ,[n-a+1,n]，共 n-a+1 种可能。

• m 行中选连续 b 行构成方形， 同理有 m-b+1 种情况。 所以 n × m 的长方形中可容纳 (n-a+1)×(m-b+1) 个 a×b 的矩形。

对于边长 k， 只有长等于宽， 才能构成正方形；其余均为长方形。

如果 a=b， 就计入正方形。 使用循环枚举 a 、b， 累加求和即可

 1 //枚举两条边 时间复杂度O(n*m)
 2 #include<bits/stdc++.h>
 3 using namespace std;
 4 typedef long long LL;
 5 int main(){
 6     int n,m;
 7     LL squ=0,rec=0;
 8     cin>>n>>m;
 9     for(int a=1;a<=n;a++)
10         for(int b=1;b<=m;b++)
11             if(a==b)
12                 squ+=(n-a+1)*(m-b+1);
13             else
14                 rec+=(n-a+1)*(m-b+1);
15     cout<<squ<<" "<<rec<<endl;
16     return 0;
17 }

---

---

还可以再快！！！

思路 5：沿用刚才乘法原理的思想，枚举量还可进一步减少？

在 n × m 的长方形中的矩形个数， 等价于在 m+1 条行线中选首尾 2 行、在 n+1 条列线中选首尾 2 列所围成的方形数目！

           

在 n+1 列中选 2 列线围长方形，左列 n+1 种情况 ；右线列不能和 左列线重复， 只有 n 种情况，将他们乘起来。

由于重复统计 (左右和右左)，要除以2，有 1/2n(n + 1) 种可能。 同理，行有 1/2m(m + 1) 种可能。一共1/4 m(m + 1) n （n+1）矩形。

借助思路4， 去掉其中的正方形。时间复杂度降到 O(min(m, n))。

 1 //枚举一条边 时间复杂度：O(n)
 2 #include<bits/stdc++.h>
 3 using namespace std;
 4 typedef long long LL;
 5 int main(){
 6     int n,m;
 7     LL squ=0,rec=0;
 8     cin>>n>>m;
 9     for(int a=1;a<=min(n,m);a++)
10         squ+=(n-a+1)*(m-a+1);
11     rec=(n+1)*n*(m+1)*m/4-squ;
12     cout<<squ<<" "<<rec<<endl;
13     return 0;
14 }

写出这样的代码还需要担心不能AC吗？

完结撒花！！！

码字不易，点个赞再走吧。