NOIP提高组模拟赛26

A. LCIS

蓝书原题，CF10D 弱化版

首先直接把 LIS 和 LCS 合起来设计一个 DP .

设 \(dp_{i,j}\) 表示 \(A_{1\dots i}\) 和 \(B_{1\dots j}\) 的以 \(B_j\) 结尾的 LCIS，则：

\[dp_{i,j}=\begin{cases}\displaystyle \max_{k<j, B_k<B_j}\{dp_{i-1,k}\}&A_i=B_j\\dp_{i-1,j}&A_i\neq B_j\end{cases}
\]

这样是 \(O(n^3)\) 的，肯定过不去（UPD. Eafoo 说能过）

然而因为 \(A_i=B_j\)，我们可以把上面那个带 max 的转移里 \(B_j\) 换成 \(A_i\)，这样可以发现当 \(i\) 一定时 max 只增不减，于是用一个变量记录一下，这样就是 \(O(n^2)\) 的了 .

using namespace std;
typedef pair<int, int> pii;
const int N = 3456, INF = 0x3f3f3f3f;
typedef long long ll;
int n, a[N], b[N], dp[N][N];
int main()
{
	scanf("%d", &n);
	for (int i=1; i<=n; i++) scanf("%d", a+i);
	for (int i=1; i<=n; i++) scanf("%d", b+i);
	for (int i=1, val; i<=n; i++)
	{
		val = 1;
		for (int j=1; j<=n; j++)
		{
			dp[i][j] = dp[i-1][j];
			if (a[i] > b[j]) chkmax(val ,dp[i-1][j] + 1);
			if (a[i] == b[j]) chkmax(dp[i][j], val);
		}
	}
	int ans = 0;
	for (int i=1; i<=n; i++) chkmax(ans, dp[n][i]);
	printf("%d\n", ans);
	return 0;
}

B. 物流运输

[ZJOI2006] 物流运输

口胡大师，思维混乱人.jpg

代码写一会推翻一段写一会推翻一段，，，，

顺便提一下，这题是 BZOJ #1003，题号还挺小 XD

---

看来我的做法是完全有问题了 /ll（UPD. 我做法好像类似 link 应该还能抢救一下），下面复读一下正解：

首先处理出时刻 \(i\sim j\) 都可以走的最短路长度 \(dis_{i,j}\)，可以 SPFA 暴力 .

然后 DP 即可，令 \(dp_i\) 表示到第 \(i\) 天的答案，枚举一个 \(j\) 然后换即可，转移方程：

\[dp_i=\max\{i\cdot dis_{1,i}, \max_{0\le j<i}\{dp_j+(i-j)dis_{j+1,i} + k\}\}
\]

DP 部分 \(O(n^2)\) .

总时间复杂度最坏是 \(O(n^2me)\) 的，如果最短路用 Dijkstra 那么复杂度就是 \(O(n^2m\log e)\) .

using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int N = 1111;
const ll INF = 0x3f3f3f3f3f3fll;
typedef long long ll;
struct dsu
{
	int fa[N];
	dsu(){reset();}
	int get(int x){return x == fa[x] ? x : fa[x] = get(fa[x]);}
	inline void merge(int x, int y){fa[get(x)] = get(y);}
	inline void reset(){iota(fa, fa+N, 0);}
}D;
int n, m, k, e, d, deg[N];
bitset<N> bb[N];
ll dist[N][N];
vector<pii> g[N];
inline void addedge(int u, int v, int w){g[u].emplace_back(make_pair(v, w));}
inline void ade(int u, int v, int w){addedge(u, v, w); addedge(v, u, w);}
ll dis[N];
bool vis[N];
inline void spfa(bitset<N> cannot)
{
	memset(vis, false, sizeof vis);
	memset(dis, 0x3f, sizeof dis);
	queue<int> q; vis[1] = true; dis[1] = 0; q.push(1);
	while (!q.empty())
	{
		int u = q.front(); q.pop();
		for (auto e : g[u])
		{
			int v = e.first, w = e.second;
			if (cannot[v]) continue;
			if (dis[v] > dis[u] + w){dis[v] = dis[u] + w;  if (!vis[v]) q.push(v), vis[v] = true;}
		} vis[u] = false;
	}
}
inline void prework()
{
	bitset<N> tmpb;
	for (int i=1; i<=n; i++)
		for (int j=i; j<=n; j++)
		{
			for (int k=1; k<=n; k++) tmpb[k] = 0;
			for (int k=i; k<=j; k++) tmpb |= bb[k];
			spfa(tmpb);
			if (dis[m] == dis[0]) dist[i][j] = INF;
			else dist[i][j] = dis[m];
		}
}
ll dp[N];
int main()
{
#ifndef ONLINE_JUDGE
	freopen("i.in", "r", stdin);
#endif
	scanf("%d%d%d%d", &n, &m, &k, &e); // m 是点数 m 是点数 m 是点数 m 是点数 m 是点数
	for (int i=0, u, v, w; i<e; i++) scanf("%d%d%d", &u, &v, &w), ade(u, v, w);
	scanf("%d", &d);
	for (int i=0, p, a, b; i<d; i++){scanf("%d%d%d", &p, &a, &b); for (int j=a; j<=b; j++) bb[j][p] = 1;}
	prework();
	for (int i=0; i<=n; i++) dp[i] = INF;
	for (int i=1; i<=n; i++)
	{
		dp[i] = dist[1][i] * i;
		for (int j=1; j<i; j++) chkmin(dp[i], dp[j] + dist[j+1][i] * (i - j) + k);
	} printf("%lld\n", dp[n]);
	return 0;
}

C. tree

[国家集训队]Tree I

这题好神啊，然而 Eafoo 场切了 .

考虑给每条白边都加上一个偏移量 \(k\)（\(k\) 可以是负的）

那么我们再算 MST 的话就肯定 \(k\) 大白边就少，\(k\) 小白边就多了 .

然后我们是要正好 \(need\) 条白边，于是我们二分这个 \(k\)，每次暴力 Kruskal 算 MST 然后数白边数量和 \(need\) 比较就好了 .

时间复杂度 \(O(n\log m)\)，附带一个二分的常数 .

然后还有两个小细节：

1. 如果边的长度一样优先选白边（双关键字排序，典）
2. 这个 \(need\) 不一定能取到，此时要取最小的大于 \(need\) 的答案 .

关于这个情况 2，例子贺一下 Eafoo 的：

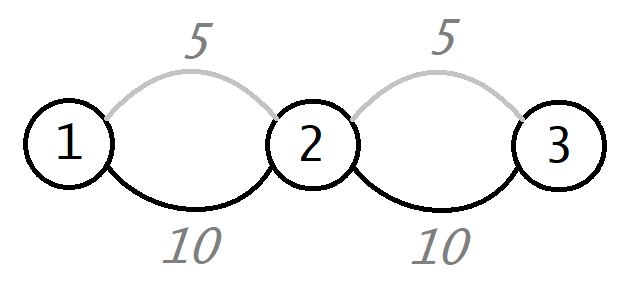
浅色是白边，深色是黑边 .

如果 \(need=1\)，注意到这个 \(k\) 不管取多少 MST 中的白边都是 \(0\) 或 \(2\)（不要说什么 MST 不唯一之类的话，情况 1 保证了白边优先）

这样肯定就是有黑白边边权相同的情况了，所以可以直接替换掉，具体实现的时候找到这种方案然后假装它有 \(need\) 条白边正常算即可 .

using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int N = 54321, M = 123456;
int n, m, need, mst;
struct Edge
{
	int u, v, w, col;
	bool operator < (const Edge& rhs) const
	{
		if (w == rhs.w) return col < rhs.col; // 白边优先
		return w < rhs.w;
	}
}ed[M];
struct dsu
{
	int fa[N];
	dsu(){reset();}
	int get(int x){return fa[x] == x ? x : fa[x] = get(fa[x]);}
	inline void merge(int x, int y){fa[get(x)] = get(y);}
	inline void reset(){iota(fa, fa+N, 0);}
}D;
inline int kruskal()
{
	int white = 0; mst = 0;
	sort(ed, ed+m); D.reset();
	for (int i=0; i<m; i++)
	{
		int u = D.get(ed[i].u), v = D.get(ed[i].v), w = ed[i].w, col = ed[i].col;
		if (u == v) continue;
		D.merge(u, v);
		white += !col; mst += w;
	} return white;
}
inline bool check(int k)
{
	for (int i=0; i<m; i++) if (!ed[i].col) ed[i].w += k;
	int white = kruskal();
	for (int i=0; i<m; i++) if (!ed[i].col) ed[i].w -= k;
	return white >= need;
}
int main()
{
	scanf("%d%d%d", &n, &m, &need);
	for (int i=0; i<m; i++) scanf("%d%d%d%d", &ed[i].u, &ed[i].v, &ed[i].w, &ed[i].col), ++ed[i].u, ++ed[i].v;
	int l = -200, r = 200, ans = -1;
	while (l <= r)
	{
		int mid = (l + r) >> 1;
		if (check(mid)){l = mid + 1; ans = mst - mid * need;}
		else r = mid - 1;
	} printf("%d\n", ans);
	return 0;
}

D. 建造游乐园

正睿原题

显然题目等价于 \(n\) 点欧拉图个数乘上 \(\dbinom n2\) .

令 \(f_n\) 表示 \(i\) 个点的欧拉图数量，\(g_n\) 表示 \(n\) 个点度为偶数的无向图数量 .

众所周知图存在欧拉回路当且仅当没有奇点 .

于是考虑加一个点，容斥掉不连通的

如果原图存在一个欧拉子图，那么 \(i\) 必然要连另外一方面，因为要保持性质，\(i\) 必须连奇点，于是就不连通了（\(i\) 连所有奇点） .

\(g_n\) 显然等于 \(2^{\tbinom{n-1}2}\)（钦定 \(n-1\) 个点随便连，剩下那个点用来平衡奇度点），于是递推式就是

\[f_n=g_n-\sum_{i=1}^{n-1}f_ig_{n-i}\dbinom{n-1}{i-1}
\]

DP，\(O(n^2)\) .

using namespace std;
typedef pair<int, int> pii;
const int N = 2222, INF = 0x3f3f3f3f, P = 1e9+7;
typedef long long ll;
int n;
ll C[N][N], f[N], g[N];
ll qpow(ll a, ll n)
{
	ll ans = 1;
	while (n)
	{
		if (n&1) ans = ans * a % P;
		a = a * a % P; n >>= 1;
	} return ans;
}
int main()
{
	C[0][0] = 1;
	for (int i=1; i<N; i++)
	{
		C[i][0] = 1;
		for (int j=1; j<=i; j++) C[i][j] = (C[i-1][j] + C[i-1][j-1]) % P;
	}
	scanf("%d", &n);
	for (int i=1; i<=n; i++) g[i] = qpow(2, C[i-1][2]);
	for (int i=1; i<=n; i++)
	{
		f[i] = g[i];
		for (int j=1; j<i; j++) f[i] = (f[i] - f[j] * g[i-j] % P * C[i-1][j-1] % P + P) % P;
	} printf("%lld\n", f[n] * C[n][2] % P);
	return 0;
}

---

下面说一下 \(O(n\log n)\) 做法 .

让我们快进到 DP .

zero4338 是一眼看穿了这题的做法的 .

首先一个关键点：度数都为偶数的图可以分成若干个欧拉图，于是欧拉图计数完全等价于连通图计数 .

考虑 exp 的组合意义，因为普通图可以划分成若干个连通图 , 所以普通图是连通图的 exp , 连通图就是普通图的 ln .

根据快进了的 DP 环节，我们知道连通图的方案数就是 \(g_n\) .

所以令 \(f_n\) 的 EGF 为 \(F(z)\)，\(g_n\) 的 EGF 为 \(G(z)\)，则

\[F=\ln G
\]

\(G\) 可以线性预处理，一次多项式 \(\ln\) 求出 \(F\)，\(O(n\log n)\) .

然而不得不谈的是模数是 \(10^9+7\)，我们仔细探讨一下过程，发现这个是完全依赖于任意模数多项式乘法的，直接 MTT 即可，还是 \(O(n\log n)\) .

然而这个带标号欧拉图计数就是 OEIS A033678 .