各种查找算法的选用分析（顺序查找、二分查找、二叉平衡树、B树、红黑树、B+树）

顺序查找
二分查找
二叉平衡树
B树
- 红黑树
B+树
参考文档

顺序查找

给你一组数，最自然的效率最低的查找算法是顺序查找——从头到尾挨个挨个遍历查找，它的时间复杂度为O(n)。

二分查找

而另一个大家都知道的，效率很高经典查找算法——二分查找法，它的时间复杂度是O(logn)。但二分法的数据结构是数组，这样才能通过公式(low+height)/2=middle计算出中间位置的元素。而数组的修改效率很低，最坏的情况下，插入一个元素，要移动n个元素。

二叉平衡树

通过模拟二分查找法的插入、查找过程，会发现和二叉平衡树很相似，那我们分析一下二叉平衡树。简单的二叉树无法保证能保证查找的每一步节点是二分法中的中间位置，最坏情况会蜕变为顺序查找。所以需要对二叉树进行调整，让它变成二叉平衡树，这样查找的效率就能保证了，二叉平衡树的查找时间复杂度也是O(logn)。但是二叉平衡树的缺点在于，调整的消耗很大。它的每次插入，都要一层一层往上确认、调整。

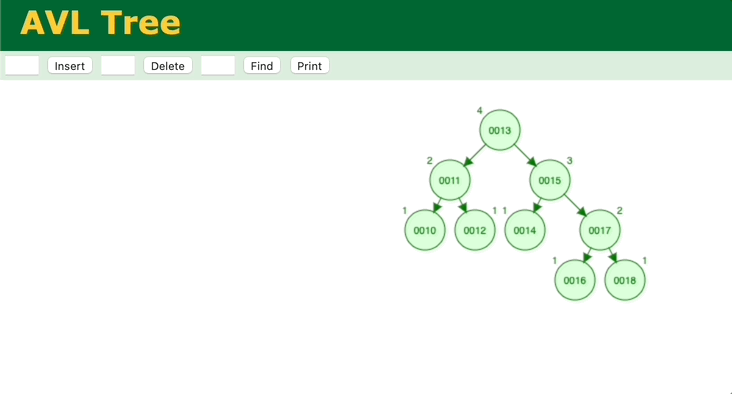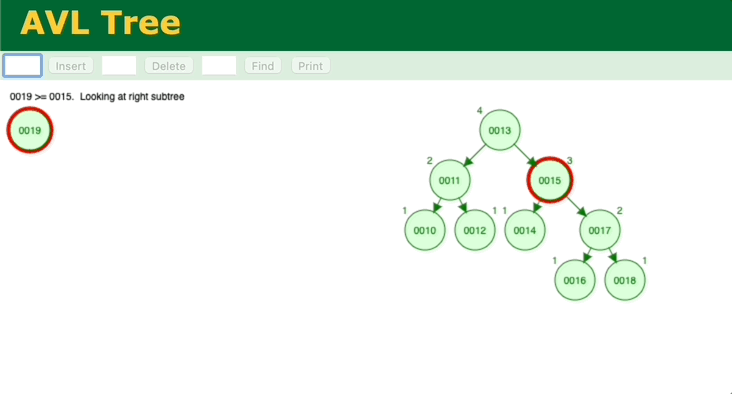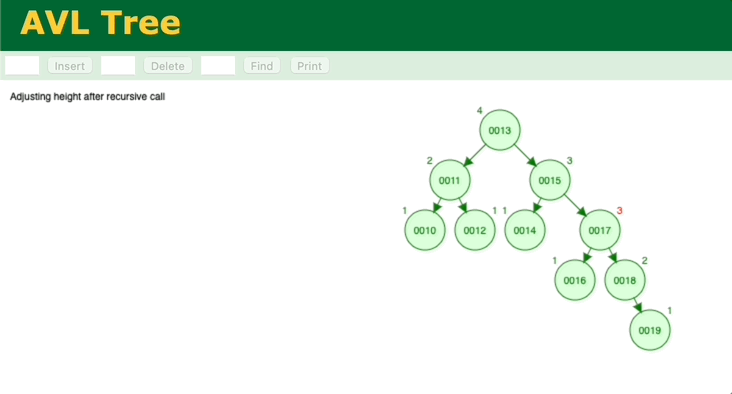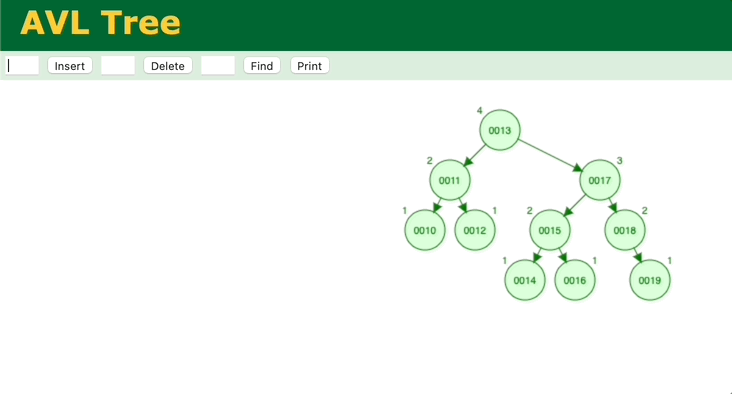
图二叉树的插入、调整过程

B树

我们再来看另外一个二叉查找树——B树。观察一下B树的插入过程。

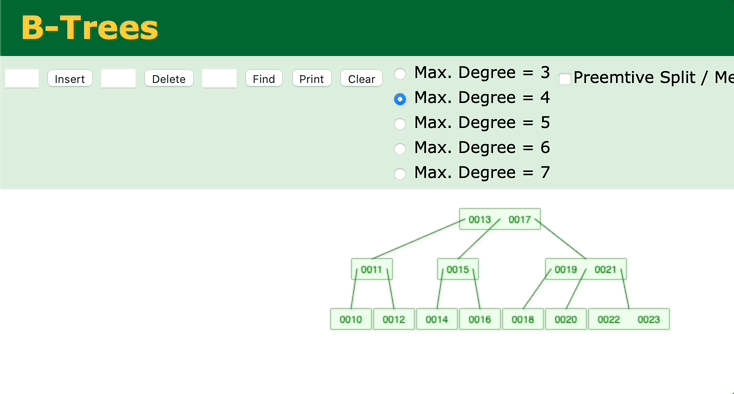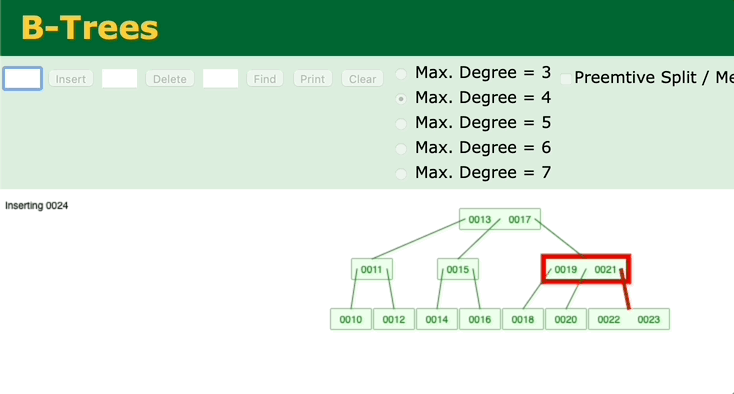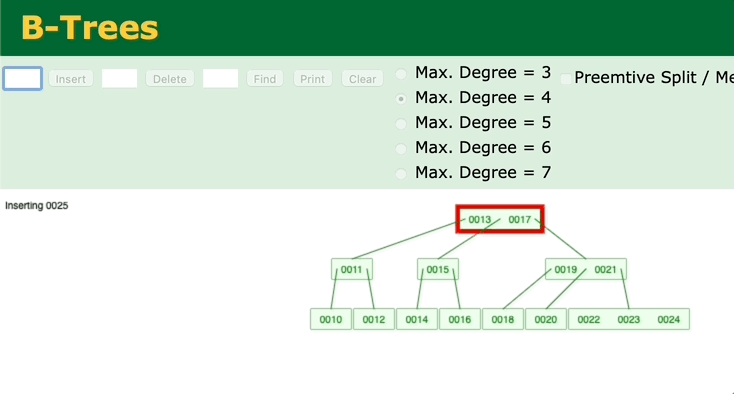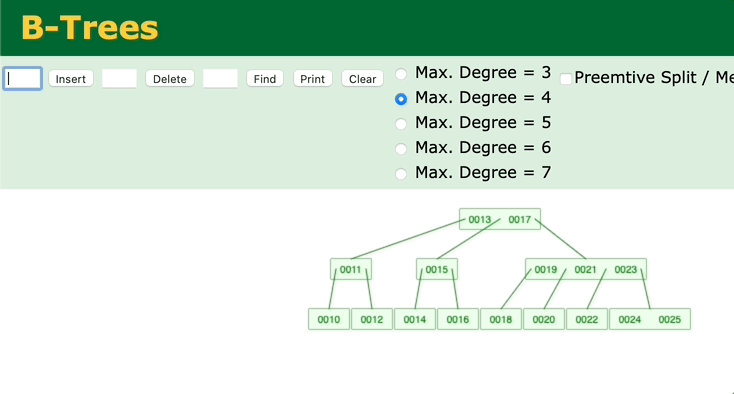
图 B树的插入、调整过程

可以看到，只有在插入后键值数超过最大键值数时，才会去修改父节点。如果父节点的中的键值数没有超过最大键值的话，就不会去动祖父节点了。所以B树的调整效率比二叉平衡树更高。

B树的另一个很大的应用是查找放在磁盘中的数据，比如数据库中数据的查找。假设现在有1G的数据，这么大的数据肯定不可能放在内存中，必须持久化到硬盘中。假设有100W条数据，使用二叉平衡树的话树高为20，即最坏情况下要进行20次I/O。如果使用64阶B树，即最坏情况下也只需要进行4次I/O就能完成查找。这就是为什么涉及到硬盘I/O的查找数据结构一般都会考虑B树。

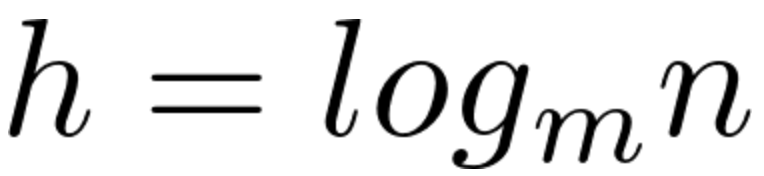
图树高计算公式（m：树的分支树 n：节点数）

红黑树

我们常听到的红黑树，它的本质其实就是对概念模型：阶数为4的B树——“2-3-4树”的一种实现。由于直接进行不同节点间的转化会造成较大的开销，所以选择以二叉树为基础，在二叉树的属性中加入一个颜色属性来表示2-3-4树中不同的节点。

详见：《红黑树原理、查找效率、插入及变化规则分析》

B+树

B+树是B树的一种变形形式，和B树的区别在于：

B+树的非叶子节点只保存索引不保存数据，叶子结点存储关键字以及相应记录的地址；
B+树的叶子节点之间会有指针

图 B+树

MySQL的存储引擎InnoDB就采用B+Tree的数据结构存储索引。B+树相比于B树的优点是：

磁盘读写代价更低

B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了；
查询效率更加稳定

由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当；
B+树便于范围查询（最重要的原因，范围查找是数据库的常态）

B树在提高了IO性能的同时并没有解决元素遍历的我效率低下的问题，正是为了解决这个问题，B+树应用而生。B+树只需要去遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的，而B树不支持这样的操作或者说效率太低（B树的范围查找用的是中序遍历，而B+树用的是在链表上遍历）。

三层B+树就可以存储千万级别的数据，详细分析过程见：B+树能存多少数据？。

参考文档