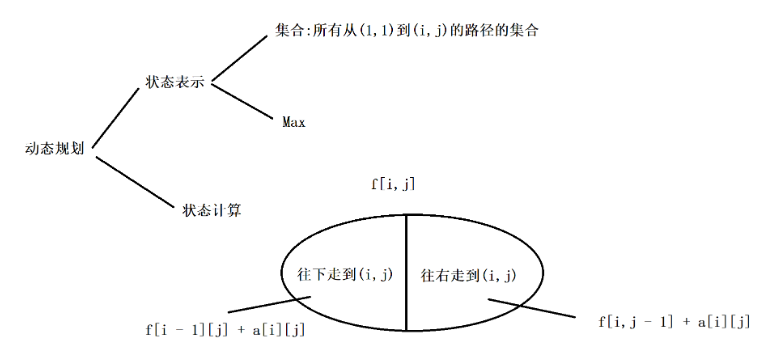
dp-位移模型(数字三角形演变)

由数字三角形问题演变而来下面的题：

https://www.cnblogs.com/sxq-study/p/12303589.html

一：规定位移方向

题目：

Hello Kitty想摘点花生送给她喜欢的米老鼠。

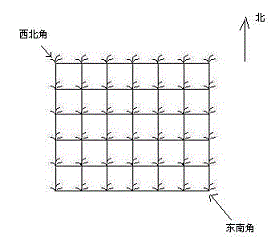
她来到一片有网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。

地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。

Hello Kitty只能向东或向南走，不能向西或向北走。

问Hello Kitty最多能够摘到多少颗花生。

输入格式

第一行是一个整数T，代表一共有多少组数据。

接下来是T组数据。

每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。

每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生苗上的花生数目M。

输出格式

对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。

数据范围

1≤T≤1001≤T≤100,
1≤R,C≤1001≤R,C≤100,
0≤M≤10000≤M≤1000

输入样例：

2
2 2
1 1
3 4
2 3
2 3 4
1 6 5

输出样例：

8
16

分析：

代码：

 1 #include <iostream>
 2 #include <algorithm>
 3
 4 using namespace std;
 5
 6 const int N = 110;
 7
 8 int n, m;
 9 int w[N][N];
10 int f[N][N];
11
12 int main()
13 {
14     int T;
15     scanf("%d", &T);
16     while (T -- )
17     {
18         scanf("%d%d", &n, &m);
19         for (int i = 1; i <= n; i ++ )
20             for (int j = 1; j <= m; j ++ )
21                 scanf("%d", &w[i][j]);
22
23         for (int i = 1; i <= n; i ++ )
24             for (int j = 1; j <= m; j ++ )
25                 f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];
26
27         printf("%d\n", f[n][m]);
28     }
29
30     return 0;
31 }

二：没有直接给出位移方向

题目：

一个商人穿过一个N×N的正方形的网格，去参加一个非常重要的商务活动。

他要从网格的左上角进，右下角出。

每穿越中间1个小方格，都要花费1个单位时间。

商人必须在(2N-1)个单位时间穿越出去。

而在经过中间的每个小方格时，都需要缴纳一定的费用。

这个商人期望在规定时间内用最少费用穿越出去。

请问至少需要多少费用？

注意：不能对角穿越各个小方格（即，只能向上下左右四个方向移动且不能离开网格）。

输入格式

第一行是一个整数，表示正方形的宽度N。

后面N行，每行N个不大于100的整数，为网格上每个小方格的费用。

输出格式

输出一个整数，表示至少需要的费用。

数据范围

1≤N≤1001≤N≤100

输入样例：

5
1  4  6  8  10
2  5  7  15 17
6  8  9  18 20
10 11 12 19 21
20 23 25 29 33

输出样例：

109

样例解释

样例中，最小值为109=1+2+5+7+9+12+19+21+33。

分析：本题通过2n-1限制了位移方向，一个n行n列的方阵，不存在斜着走的情况下，从左上角走到右上角最小的步数就是 2n-1， 并且只能向右或者向下走， 也就是不存在回头的情况

代码：

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 using namespace std;
 5
 6 const int N = 110, INF = 0x3f;
 7
 8 int dp[N][N];
 9 int g[N][N];
10
11 int n;
12
13 int main(){
14     cin >> n;
15     for(int i = 1;i <= n;++i)
16         for(int j = 1;j <= n;++j)
17             cin >> g[i][j];
18
19     memset(dp, INF, sizeof dp);
20
21     for(int i = 1;i <= n;++i)
22         for(int j = 1;j <= n;++j)
23             if(i == 1 && j == 1)
24                 dp[1][1] = g[1][1];
25             else
26                 dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + g[i][j];
27
28     cout << dp[n][n] << endl;
29 }

三：两次从左上角到右下角的最大价值

题目：

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

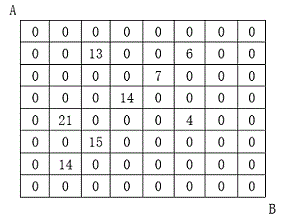
某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。

在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

输入格式

第一行为一个整数N，表示 N×N 的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。

一行“0 0 0”表示结束。

输出格式

输出一个整数，表示两条路径上取得的最大的和。

数据范围

N≤10N≤10

输入样例：

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

输出样例：

67

思路分析：

1：首先想出状态表示，dp[i1][j1][i2][j2]表示从起点到(i1, j1)和(i2, j2)的所有走法的集合，集合的属性就表示最大价值
2：状态压缩，对于 n * m 的矩阵来说，如果规定位移方向只能向下或者向右，那么很容易想出从左上角走到右下角的总共走的步数一定是 n+m ，所以我们可以省略其中一维的下标j,用k（总步数）- i 来代表j，所以新的dp为 dp[k][i1][i2]
3：思考集合划分，划分依据是最后一步，可能来自四种情况
　　(1):第一条路径来自左，第二条来自左 dp[k-1][i1][i2]
　　(2):第一条路径来自左，第二条来自上 dp[k-1][i1][i2-1]
　　(3):第一条路径来自上，第二条来自上 dp[k-1][i1-1][i2-1]
　　(4):第一条路径来自上，第二条来自左 dp[k-1][i1-1][i2]
4: 最后一步思考初始条件以及枚举方向
　　初始条件：dp数组全部为0即可
　　枚举方向：从小到大，因为保证用到的的状态计算过

代码：

 1 #include <iostream>
 2 #include <algorithm>
 3 using namespace std;
 4
 5 const int N = 15;
 6
 7 int g[N][N];
 8 int dp[N+N][N][N];
 9 int n;
10
11 int main(){
12     cin >> n;
13     int a, b, c;
14     while(cin >> a >> b >> c, a || b || c) g[a][b] = c;
15     for(int k = 2;k <= n + n;++k){
16         for(int i1 = 1;i1 <= n;++i1){
17             for(int i2 = 1;i2 <= n;++i2){
18                 int j1 = k - i1, j2 = k-i2;
19                 if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n){//找到满足条件的状态
20                     int &t = dp[k][i1][i2];
21                     int w = (i1 == i2 ? g[i1][j1] : (g[i1][j1] + g[i2][j2]));
22                     t = max(t, dp[k-1][i1-1][i2-1] + w);
23                     t = max(t, dp[k-1][i1][i2] + w);
24                     t = max(t, dp[k-1][i1-1][i2] + w);
25                     t = max(t, dp[k-1][i1][i2-1] + w);
26                 }
27             }
28         }
29     }
30     cout << dp[n+n][n][n] << endl;
31     return 0;
32 }