百度松果菁英班OJ【连载】

第十六周

2 的 n 次幂

• 高精度乘法

#include<bits/stdc++.h> 

using namespace std;

vector<int> mul(vector<int> &A) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || t; i++) {
        if (i < A.size()) t += A[i] * 2;
        C.push_back(t % 10);
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main()
{
    int n;
    cin >> n;
    vector<int> A;
    A.push_back(1);
    while (n--) {
        A = mul(A);
    }
    for (int i = A.size() - 1; i >= 0; i--) {
        printf("%d", A[i]);
    }
    return 0;
}

个数统计

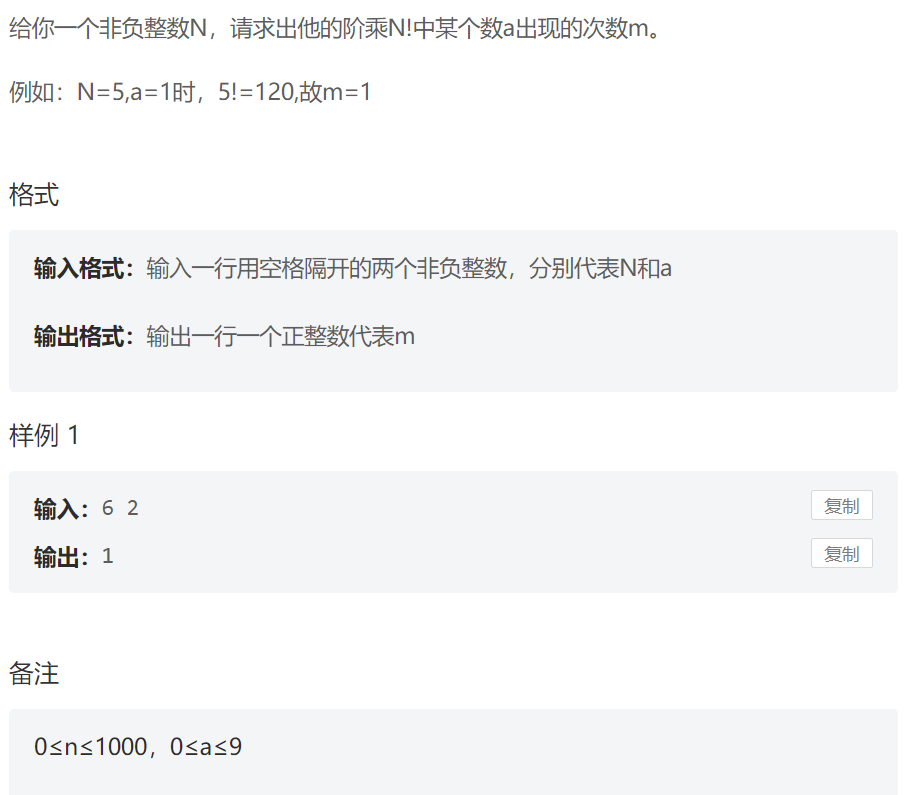
• 高精度乘法求阶乘
• 个数统计

#include<bits/stdc++.h> 

using namespace std;

vector<int> mul(vector<int> &A, int x) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || t; i++) {
        if (i < A.size()) t += A[i] * x;
        C.push_back(t % 10);
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main( )
{
    int N, a;
    cin >> N >> a;
    vector<int> A;
    A.push_back(1);
    for (int i = 2; i <= N; i++) {
        A = mul(A, i);
    }
    int ans = 0;
    for (int i = A.size() - 1; i >= 0; i--) {
        if (A[i] == a) ans++;
    }
    cout << ans << endl;
    return 0;
}

数组扞插

题目复述：

• 将数组分为三部分，前半段，后半段，和中间的数（如果数组大小是奇数）
• 前半段升序排列
• 后半段降序排列
• 如果有中间的数字，则中间的数不参与排列，直接放到结果数组的末尾

#include<bits/stdc++.h> 

using namespace std;

int n;
const int N = 10010;
int a[N], b[N];

int main( )
{
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    int l = n + 1 >> 1; // 前半段 + 中间数字（可能没有）
    int r = n - l;      // 后半段
    if (l == r) {       // 前后一样多
        sort(a, a + l, less<int>());
        sort(a + l, a + n, greater<int>());
    }
    else {              // 前面多一个，则中间的数不参与排序
        sort(a, a + l - 1, less<int>());
        sort(a + l, a + n, greater<int>());
    }
    int ll = 0, rr = l;

    // 交叉插入结果数组
    for (int i = 0; i < n; i++) {
        if (i % 2 == 0) b[i] = a[ll++];
        else b[i] = a[rr++];
    }
    for (int k = 0; k < n; k++) {
        printf("%d ", b[k]);
    }
    return 0;
}

MXR 竞赛

题目复述：

• N 个问题，都有积分，范围为负数、零和正数
• 选出所有一个积分子集，使得子集中的所有积分的乘积得到最大值

解法：

• 贪心思想
• 所有积分从小到大排序，所有正数全部参与乘积
• 所有负数，相邻两个负数相乘得到正数。从左向右遍历，只要相邻两个积分是负数，则这两个负数都参与乘积；最后可能剩下一个绝对值最小的负数，不参与乘积
• 特殊情况：如果所有积分都没有选取，比如只有一个负数，返回数组最后一个数（最大）

#include<bits/stdc++.h> 

using namespace std;

const int N = 100010;
long n;
int a[N];

int main( )
{
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    long ans = 1;       // 注意精度，int 会爆精度
    int flag = 0;
    sort(a, a + n);
    for (int i = 0; i < n; i++) {
        if (a[i] < 0) {
            if (i < n - 1 && a[i + 1] < 0) {
                ans = ans * (a[i] * a[i + 1]);
                ans %= 998244353;
                i++;
                flag++;
            }
        } else if (a[i] > 0) {
            ans = ans * a[i];
            ans %= 998244353;
            flag++;
        }
    }
    if (flag == 0) printf("%d", a[n - 1]);
    else printf("%d", ans);
    return 0;
}

小码哥的跳棋游戏

题目复述：

• 没有棋子不消耗能量
• 一次最多跳过一个棋子
• 破坏一个棋子消耗一个能量
• 求消耗最小能量从 0 位置到达 n 位置

解法：

• 贪心思想 + 双指针
• 对于连续 n 个棋子，n 为奇数，最少破坏 ⌊n / 2⌋ 个棋子
• 对于连续 n 个棋子，n 为偶数，最少破坏 n / 2 个棋子
• 由于 int 除法自动取整特性，以上两种情况可以合并

#include<bits/stdc++.h> 

using namespace std;

const int N = 100010;
int a[N];

int main( )
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    int ans = 0;
    int i = 0;
    while (i < n) {
        // 出现棋子
        if (a[i] == 1) {
            int count = 1;
            int j;
            // 统计连续棋子个数
            for (j = i + 1; j < n && a[j] == 1; j++) {
                 count++;
            }
            ans += count / 2;
            // 破坏之后就可以跳动了
            i = j;
        } else {
            // 没有棋子就直接跳
            i++;
        }
    }
    // 由于跳动到第 n 块，如果第 n - 1 块是棋子，需要破坏
    if (a[n - 1] == 1) ans++;
    cout << ans;
    return 0;
}

矩阵乘法

• 常规矩阵乘法

#include<bits/stdc++.h> 

using namespace std;

const int N = 1010;
int a[N][N], b[N][N], c[N][N];
int l, m, n;
void mul(int a[][N], int b[][N]) {
    for (int i = 0; i < l; i++) {
        for (int j = 0; j < n; j++) {
            for (int k =0; k < m; k++) {
                c[i][j] += a[i][k] * b[k][j];
            }
        }
    }
}

int main( )
{
    cin >> l >> m >> n;
    for (int i = 0; i < l; i++) {
        for (int j = 0; j < m; j++) {
            scanf("%d", &a[i][j]);
        }
    }
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            scanf("%d", &b[i][j]);
        }
    }
    mul(a, b);
    for (int i = 0; i < l; i++) {
        for (int j = 0; j < n; j++) {
            printf("%d ", c[i][j]);
        }
        printf("\n");
    }
    return 0;
}