Neural Network模型复杂度之Weight Decay - Python实现

• 背景介绍
  Neural Network之模型复杂度主要取决于优化参数个数与参数变化范围. 优化参数个数可手动调节, 参数变化范围可通过正则化技术加以限制. 正则化技术之含义是: 引入额外的条件, 对function space进行适当的约束. 本文借助pytorch前向计算与反向传播特性, 以正则化技术之weight decay($l^2$范数)为例, 简要演示正则化对Neural Network模型复杂度的影响.
• 操作流程
  ①. 获取数据; ②. 封装数据; ③. 构建模型; ④. 构建损失函数; ⑤. 构建优化器; ⑥. 训练单元; ⑦. 测试单元; ⑧. 启动训练测试; ⑨. 保存模型
• 数据、模型与损失函数
  数据生成策略如下,
  \begin{equation*}
  \left\{
  \begin{aligned}
  x &= r + 2g + 3b \\
  y &= r^2 + 2g^2 + 3b^2 \\
  lv &= -3r-4g-5b
  \end{aligned}
  \right.
  \end{equation*}
  Neural Network网络模型如下,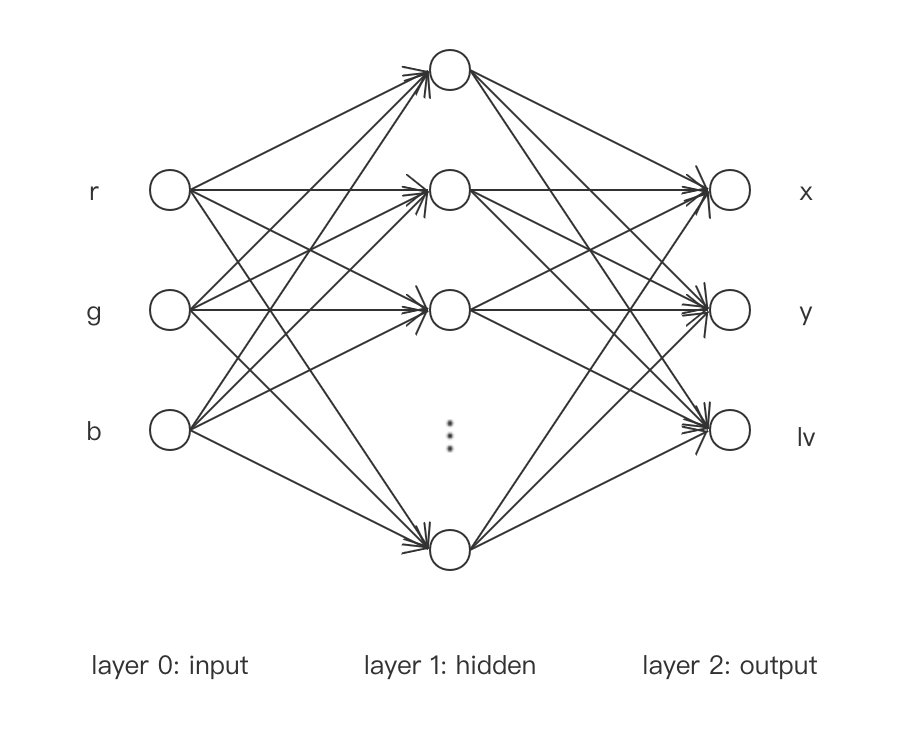
  
  其中, 输入层为$(r,g,b)$, 隐藏层取激活函数为双曲正切函数$\tanh$, 输出层为$(x,y,lv)$且不取激活函数.
  损失函数如下,
  \begin{gather*}
  L = \sum_i\frac{1}{2}(\bar{x}^{(i)}-x^{(i)})^2+\frac{1}{2}(\bar{y}^{(i)}-y^{(i)})^2+\frac{1}{2}(\bar{lv}^{(i)}-lv^{(i)})^2 \\
  J = L + \frac{\lambda}{2}\|W\|_2^2
  \end{gather*}
  其中, $i$为data序号, $(\bar{x}, \bar{y}, \bar{lv})$为相应观测值, $W$为隐藏层weight, $L$为原始损失函数, $J$为添加$W$之$l^2$正则项后的损失函数, $\lambda$为可调超参数控制正则项在损失函数$J$中的权重.
• 代码实现
  本文拟将中间隐藏层节点数设置为50, 使模型具备较高复杂度. 后逐渐提升权重参数$\lambda$, 使模型复杂度降低, 以此观察泛化误差的变化. 根据操作流程, 具体实现如下,
  
  

    1 # L2 normalization之实现:
    2 # 1. 获取数据
    3 # 2. 封装数据
    4 # 3. 构建模型
    5 # 4. 构建损失函数
    6 # 5. 构建优化器
    7 # 6. 训练单元
    8 # 7. 测试单元
    9 # 8. 启动训练与测试
   10 # 9. 保存模型
   11
   12 import numpy
   13 import torch
   14 from torch import optim
   15 from matplotlib import pyplot as plt
   16
   17
   18 numpy.random.seed(0)
   19 torch.random.manual_seed(0)
   20
   21 def xFunc(r, g, b):
   22     x = r + 2 * g + 3 * b
   23     return x
   24
   25 def yFunc(r, g, b):
   26     y = r ** 2 + 2 * g ** 2 + 3 * b ** 2
   27     return y
   28
   29 def lvFunc(r, g, b):
   30     lv = -3 * r - 4 * g - 5 * b
   31     return lv
   32
   33
   34 # 1. 获取数据
   35 class GeneData(object):
   36
   37     def __init__(self, rRange=[-1, 1], gRange=[-1, 1], bRange=[-1, 1]):
   38         self.__rRange = rRange
   39         self.__gRange = gRange
   40         self.__bRange = bRange
   41
   42     def getDataset(self, num):
   43         rArr, gArr, bArr = self.__generate_rgbArr(num)
   44         xArr, yArr, lvArr = self.__generate_xylvArr(rArr, gArr, bArr)
   45         rgb = numpy.hstack((rArr.reshape((-1, 1)), gArr.reshape((-1, 1)), bArr.reshape((-1, 1))))
   46         xylv = numpy.hstack((xArr.reshape((-1, 1)), yArr.reshape((-1, 1)), lvArr.reshape((-1, 1))))
   47         return torch.tensor(rgb, dtype=torch.float), torch.tensor(xylv, dtype=torch.float)
   48
   49     def __generate_xylvArr(self, rArr, gArr, bArr):
   50         xArr = xFunc(rArr, gArr, bArr)
   51         yArr = yFunc(rArr, gArr, bArr)
   52         lvArr = lvFunc(rArr, gArr, bArr)
   53         return xArr, yArr, lvArr
   54
   55     def __generate_rgbArr(self, num):
   56         rArr = numpy.random.uniform(*self.__rRange, num)
   57         gArr = numpy.random.uniform(*self.__gRange, num)
   58         bArr = numpy.random.uniform(*self.__bRange, num)
   59         return rArr, gArr, bArr
   60
   61
   62 # 2. 封装数据
   63 class PackData(object):
   64
   65     def __init__(self, features, labels, batch_size=None, random_shuffle=True):
   66         self.__features = features
   67         self.__labels = labels
   68         self.__batch_size = batch_size
   69         self.__random_shuffle = random_shuffle
   70
   71         self.num = self.__features.shape[0]
   72         if self.__batch_size is None:
   73             self.__batch_size = self.num
   74
   75         self.__indices = list(range(self.num))
   76         if self.__random_shuffle:
   77             numpy.random.shuffle(self.__indices)
   78
   79     def __call__(self):
   80         for i in range(0, self.num, self.__batch_size):
   81             batchIndices = self.__indices[i:min(i+self.__batch_size, self.num)]
   82             yield self.__features[batchIndices], self.__labels[batchIndices]
   83
   84
   85 # 3. 构建模型: multi-layer perceptron
   86 class MLP(object):
   87
   88     def __init__(self, hidden_dim=100):
   89         self.__hidden_dim = hidden_dim
   90
   91         self.l1_W = torch.normal(0, 0.01, (3, self.__hidden_dim), requires_grad=True)
   92         self.l1_b = torch.zeros((1, self.__hidden_dim), requires_grad=True)
   93         self.l1_f = torch.nn.Tanh()
   94
   95         self.l2_W = torch.normal(0, 0.01, (self.__hidden_dim, 3), requires_grad=True)
   96         self.l2_b = torch.zeros((1, 3), requires_grad=True)
   97
   98     def __call__(self, x):
   99         l1_1 = torch.matmul(x, self.l1_W) + self.l1_b
  100         l1_2 = self.l1_f(l1_1)
  101
  102         l2_1 = torch.matmul(l1_2, self.l2_W) + self.l2_b
  103         return l2_1
  104
  105
  106 # 4. 构建损失函数
  107 class MSE(object):
  108
  109     def __init__(self, lamda):
  110         self.__lamda = lamda
  111
  112     def __call__(self, Y, Y_, mlpObj=None):
  113         L = torch.sum((Y - Y_) ** 2) / 2
  114         if mlpObj:
  115             term1 = torch.sum(mlpObj.l1_W ** 2)
  116             term2 = torch.sum(mlpObj.l2_W ** 2)
  117             term3 = (term1 + term2) * self.__lamda / 2
  118             L = L + term3
  119         return L
  120
  121
  122 # 6. 训练单元
  123 def training_epoch(packObj, mlpObj, mseObj, optObj):
  124     loss_total = 0
  125     with torch.enable_grad():
  126         for X, Y_ in packObj():
  127             optObj.zero_grad()
  128             Y = mlpObj(X)
  129             loss = mseObj(Y, Y_, mlpObj)
  130             loss.backward()
  131             optObj.step()
  132
  133             loss_total += loss.item()
  134     return loss_total
  135
  136
  137 # 7. 测试单元
  138 def testing_epoch(packObj, mlpObj, mseObj):
  139     loss_total = 0
  140     with torch.no_grad():
  141         for X, Y_ in packObj():
  142             Y = mlpObj(X)
  143             loss = mseObj(Y, Y_)
  144             loss_total += loss.item()
  145     return loss_total
  146
  147
  148 # 8. 启动训练与测试
  149 def train(trainingData, testingData, model, loss, optimizer, maxEpoch=10000):
  150     testingLossList = list()
  151     for epoch in range(maxEpoch):
  152         training_epoch(trainingData, model, loss, optimizer)
  153         testingLoss = testing_epoch(testingData, model, loss) / testingData.num
  154         testingLossList.append(testingLoss)
  155         # if epoch % 100 == 0:
  156         #     print("epoch {}: testing error = {:.5f}".format(epoch,
  157         #         testingLoss))
  158
  159     minIdx = numpy.argmin(testingLossList)
  160     testingLossBest = testingLossList[minIdx]
  161     return testingLossBest
  162
  163
  164 # 9. 模型保存
  165 def save(model, filename=None):
  166     l1_W = model.l1_W.detach().numpy()
  167     l1_b = model.l1_b.detach().numpy()
  168     l2_W = model.l2_W.detach().numpy()
  169     l2_b = model.l2_b.detach().numpy()
  170
  171     if filename is None:
  172         filename = "./mlp.dat"
  173     with open(filename, "wt") as f:
  174         f.write("l1_W = \n")
  175         for row in l1_W:
  176             for ele in row:
  177                 f.write("{:.9f} ".format(ele))
  178             f.write("\n")
  179         f.write("\nl1_b = \n")
  180         for ele in l1_b[0]:
  181             f.write("{:.9f} ".format(ele))
  182         f.write("\n")
  183
  184         f.write("\nl2_W = \n")
  185         for row in l2_W:
  186             for ele in row:
  187                 f.write("{:.9f} ".format(ele))
  188             f.write("\n")
  189         f.write("\nl2_b = \n")
  190         for ele in l2_b[0]:
  191             f.write("{:.9f} ".format(ele))
  192
  193
  194 # 搜索超参数lamda
  195 def search_lamda():
  196     rRange = [-10, 10]
  197     gRange = [-10, 10]
  198     bRange = [-10, 10]
  199     trainingNum = 500
  200     testingNum = 1000
  201     batch_size = 250
  202     hidden_dim = 50
  203
  204     geneObj = GeneData(rRange, gRange, bRange)
  205     trainingData = geneObj.getDataset(trainingNum)
  206     testingData = geneObj.getDataset(testingNum)
  207     trainingPack = PackData(*trainingData, batch_size)
  208     testingPack = PackData(*testingData, batch_size)
  209
  210     lamda = 0.001
  211     lr = 0.003
  212     mlpObj = MLP(hidden_dim)
  213     mseObj = MSE(lamda)
  214     params = [mlpObj.l1_W, mlpObj.l1_b, mlpObj.l2_W, mlpObj.l2_b]
  215     optObj = optim.Adam(params, lr)
  216     train(trainingPack, testingPack, mlpObj, mseObj, optObj, 100000)
  217     l1_W, l1_b, l2_W, l2_b = mlpObj.l1_W, mlpObj.l1_b, mlpObj.l2_W, mlpObj.l2_b
  218
  219     lr = 0.003
  220     lamdaList = numpy.linspace(0, 0.01, 101)
  221     testList = list()
  222     for idx, lamda in enumerate(lamdaList):
  223         mlpObj = MLP(hidden_dim)
  224         mlpObj.l1_W.requires_grad = False
  225         mlpObj.l1_b.requires_grad = False
  226         mlpObj.l2_W.requires_grad = False
  227         mlpObj.l2_b.requires_grad = False
  228         l1_W.requires_grad = False
  229         l1_b.requires_grad = False
  230         l2_W.requires_grad = False
  231         l2_b.requires_grad = False
  232         mlpObj.l1_W[:], mlpObj.l1_b[:], mlpObj.l2_W[:], mlpObj.l2_b[:] = l1_W, l1_b, l2_W, l2_b
  233         mlpObj.l1_W.requires_grad = True
  234         mlpObj.l1_b.requires_grad = True
  235         mlpObj.l2_W.requires_grad = True
  236         mlpObj.l2_b.requires_grad = True
  237         mseObj = MSE(lamda)
  238         params = [mlpObj.l1_W, mlpObj.l1_b, mlpObj.l2_W, mlpObj.l2_b]
  239         optObj = optim.Adam(params, lr)
  240         testingLoss = train(trainingPack, testingPack, mlpObj, mseObj, optObj, 100000)
  241         print("lamda = {:5f}, testing error = {}".format(lamda, testingLoss))
  242         testList.append(testingLoss)
  243         l1_W, l1_b, l2_W, l2_b = mlpObj.l1_W, mlpObj.l1_b, mlpObj.l2_W, mlpObj.l2_b
  244
  245     minIdx = numpy.argmin(testList)
  246     lamdaBest = lamdaList[minIdx]
  247     testBest = testList[minIdx]
  248
  249     fig = plt.figure(figsize=(5, 4))
  250     ax1 = fig.add_subplot(1, 1, 1)
  251     ax1.plot(lamdaList, testList, ".--", lw=1, markersize=5, label="testing error", zorder=1)
  252     ax1.scatter(lamdaBest, testBest, marker="*", s=30, c="red", label="optimal", zorder=2)
  253     ax1.set(xlabel="$\\lambda$", ylabel="error", title="optimal $\\lambda$ = {:.5f}".format(lamdaBest))
  254     ax1.legend()
  255     fig.tight_layout()
  256     fig.savefig("search_lamda.png", dpi=100)
  257
  258     ############
  259     maxEpoch = 100000
  260     mlpObj = MLP(hidden_dim)
  261     mseObj = MSE(lamdaBest)
  262     params = [mlpObj.l1_W, mlpObj.l1_b, mlpObj.l2_W, mlpObj.l2_b]
  263     optObj = optim.Adam(params, lr)
  264
  265     testingLossBest = numpy.inf
  266     for epoch in range(maxEpoch):
  267         training_epoch(trainingPack, mlpObj, mseObj, optObj)
  268         testingLoss = testing_epoch(testingPack, mlpObj, mseObj) / testingPack.num
  269         print("epoch {}: testing error best = {}, testing error current = {}".format(epoch, testingLossBest, testingLoss))
  270         if testingLoss < testingLossBest:
  271             save(mlpObj)
  272             testingLossBest = testingLoss
  273
  274
  275
  276 if __name__ == "__main__":
  277     search_lamda()

• 结果展示
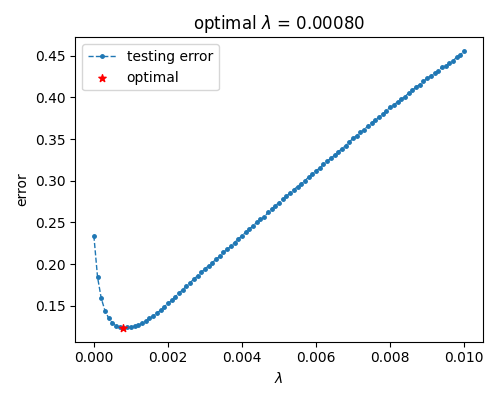  可以看到, 泛化误差在提升权重参数后先下降后上升, 大致对应降低模型复杂度使模型表现从过拟合至欠拟合.
• 使用建议
  ①. bias代表函数偏置, 直观上对模型复杂度(函数平滑程度)影响微弱, 一般无需正则化;
  ②. 超参数连续调整时, 训练参数迭代初值可选用前一超参数下的收敛值;
  ③. weight decay适用于神经网络所有层.
• 参考文档
  ①. 动手学深度学习 - 李牧