.NET二叉树，递归和迭代遍历二叉树

代码随想录: https://programmercarl.com

.NET中二叉树的定义

public class TreeNode
{
  public int val;
  public TreeNode left;
  public TreeNode right;
  public TreeNode(int val = 0, TreeNode left = null, TreeNode right = null)
  {
    this.val = val;
    this.left = left;
    this.right = right;
  }
}

二叉树的种类

满二叉树

满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

如图所示：

这棵二叉树为满二叉树，也可以说深度为k，有2^k-1个节点的二叉树。

完全二叉树

什么是完全二叉树？

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。

大家要自己看完全二叉树的定义，很多同学对完全二叉树其实不是真正的懂了。

我来举一个典型的例子如题：

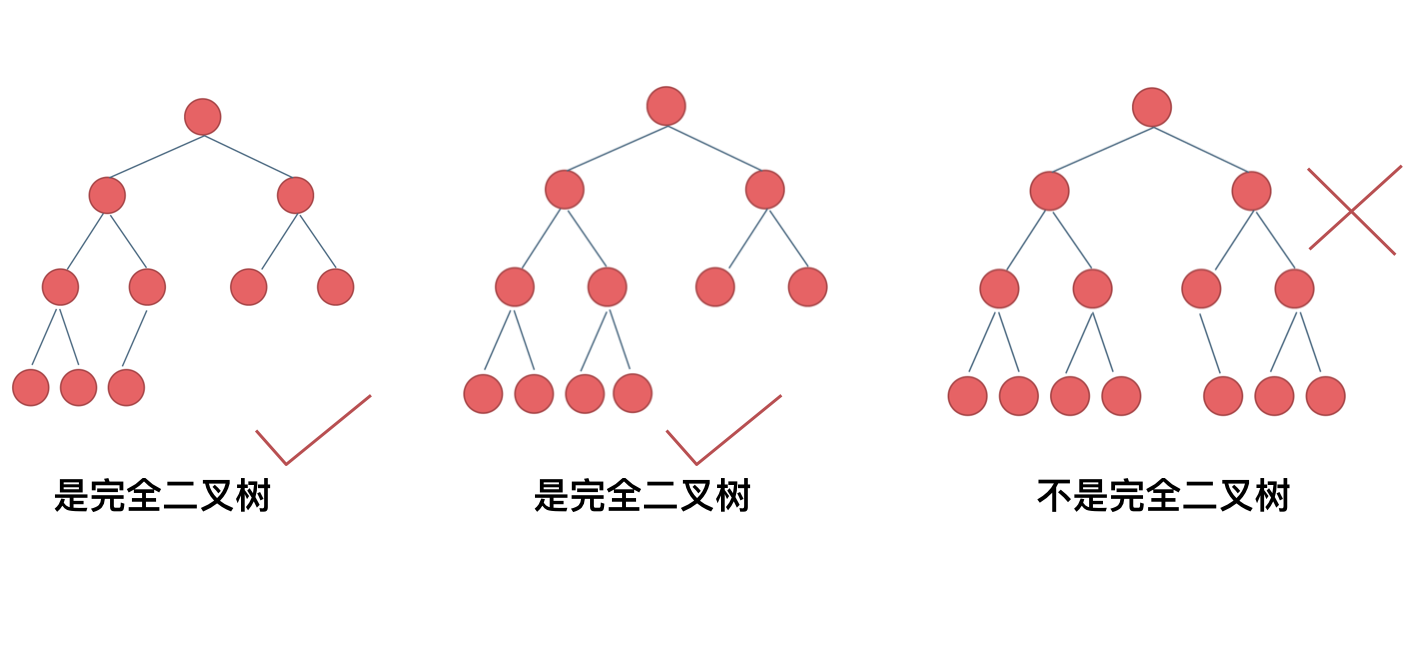
相信不少同学最后一个二叉树是不是完全二叉树都中招了。

之前我们刚刚讲过优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。

二叉搜索树

前面介绍的树，都没有数值的，而二叉搜索树是有数值的了，二叉搜索树是一个有序树。

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

它的左、右子树也分别为二叉排序树

下面这两棵树都是搜索树

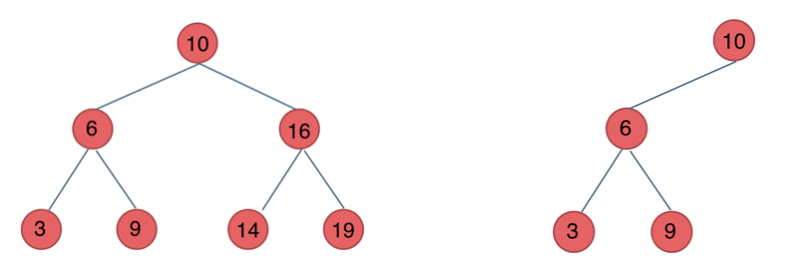
平衡二叉搜索树

平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

如图：

最后一棵 不是平衡二叉树，因为它的左右两个子树的高度差的绝对值超过了1。

C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn，注意我这里没有说unordered_map、unordered_set，unordered_map、unordered_map底层实现是哈希表。

所以大家使用自己熟悉的编程语言写算法，一定要知道常用的容器底层都是如何实现的，最基本的就是map、set等等，否则自己写的代码，自己对其性能分析都分析不清楚！

二叉树的存储方式

二叉树可以链式存储，也可以顺序存储。

那么链式存储方式就用指针， 顺序存储的方式就是用数组。

顾名思义就是顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在散落在各个地址的节点串联一起。

链式存储如图：

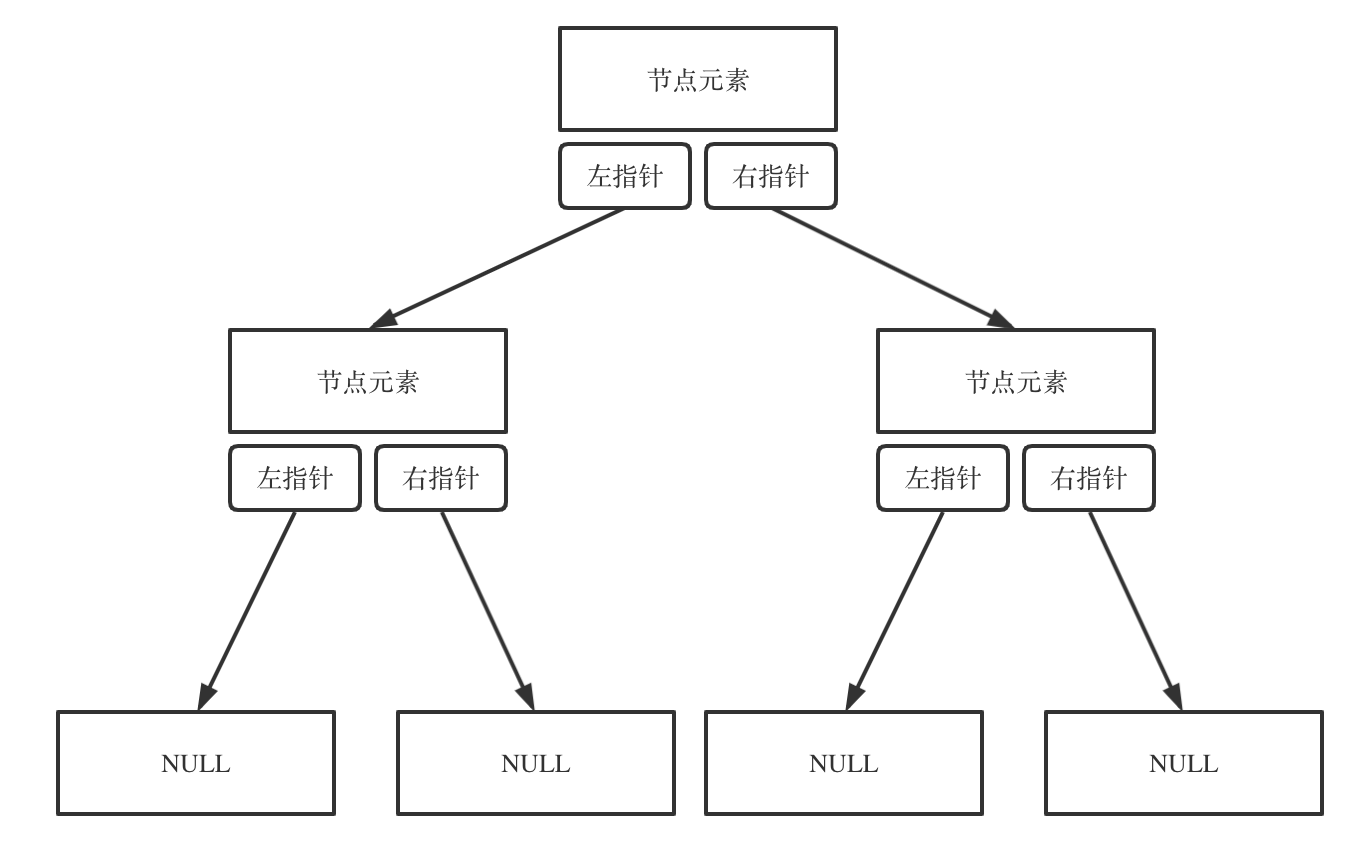
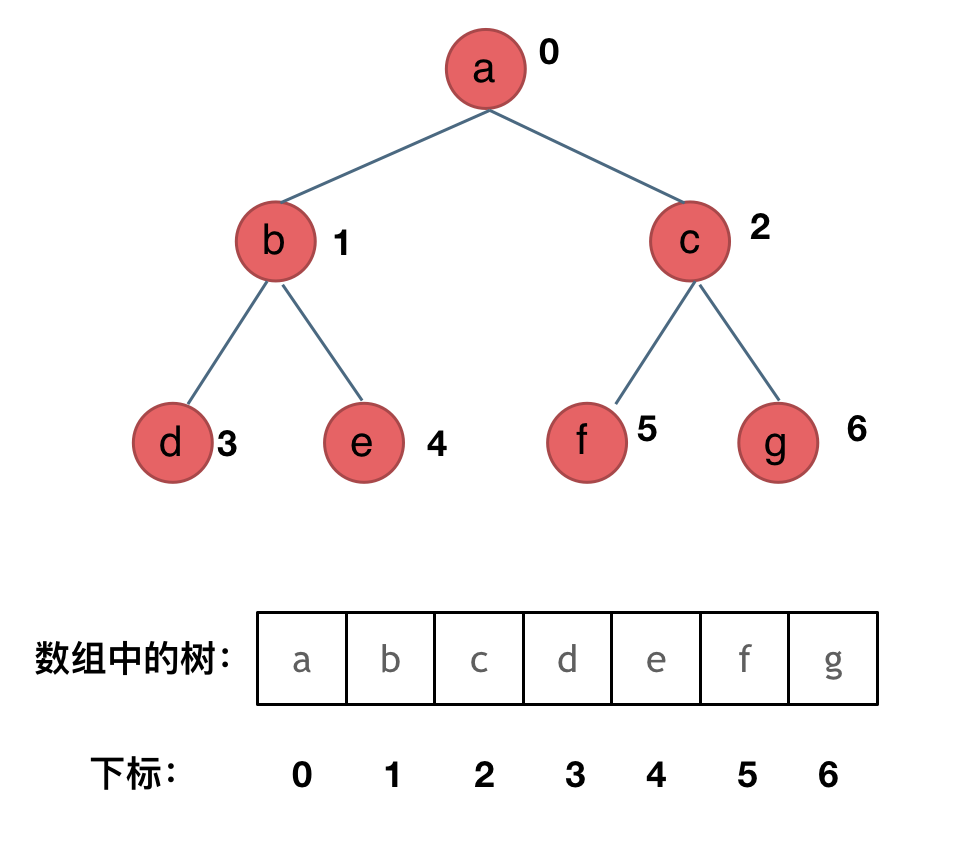
链式存储是大家很熟悉的一种方式，那么我们来看看如何顺序存储呢？

其实就是用数组来存储二叉树，顺序存储的方式如图：

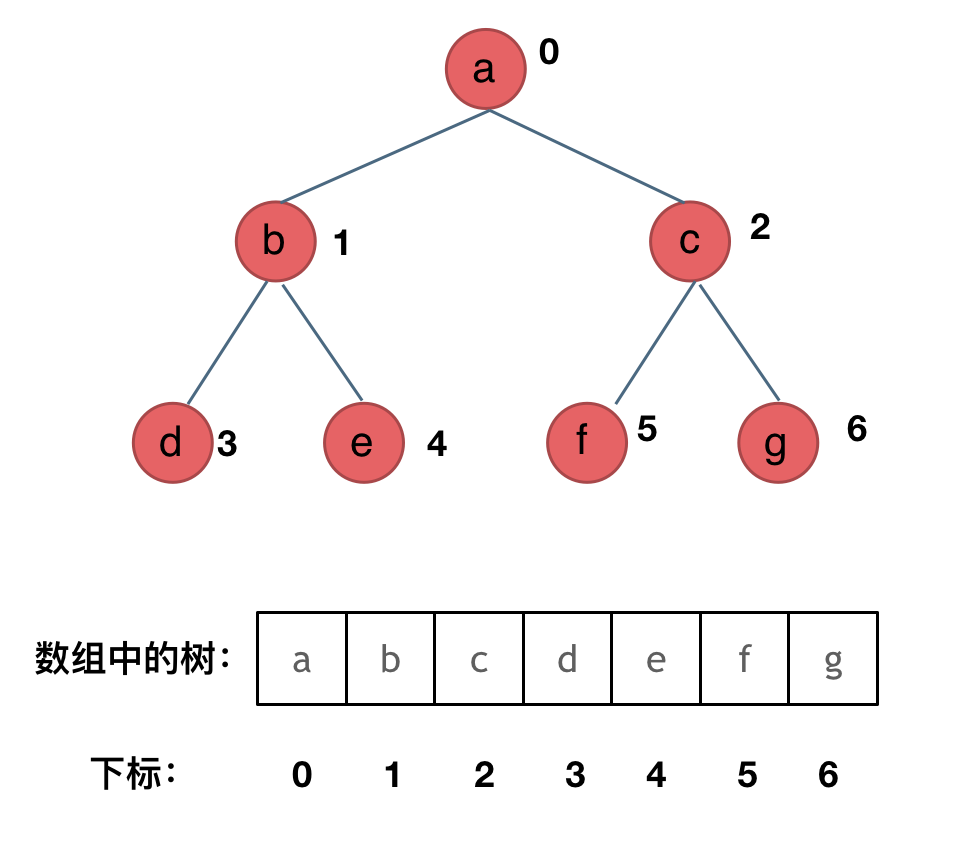
用数组来存储二叉树如何遍历的呢？

如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。

所以大家要了解，用数组依然可以表示二叉树。

递归遍历

前序遍历

/// <summary>
/// 前序遍历（中左右）
/// </summary>
/// <param name="root"></param>
/// <returns></returns>
public IList<int> PreorderTraversal(TreeNode root)
{
    List<int> result = new List<int>();
    Preorder(result, root);
    return result;
}
public void Preorder(List<int> result, TreeNode node)
{
    if (node == null) return;
    result.Add(node.val);//中
    Preorder(result, node.left);//左
    Preorder(result, node.right);//右
}

中序遍历

/// <summary>
/// 中序遍历（左中右）
/// </summary>
/// <param name="root"></param>
/// <returns></returns>
public IList<int> InorderTraversal(TreeNode root)
{
    List<int> result = new List<int>();
    Inorder(result, root);
    return result;
}
public void Inorder(List<int> result, TreeNode node)
{
    if (node == null) return;
    Inorder(result, node.left);//左
    result.Add(node.val);//中
    Inorder(result, node.right);//右
}

后序遍历

/// <summary>
/// 后序遍历（左右中）
/// </summary>
/// <param name="root"></param>
/// <returns></returns>
public IList<int> PostOrderTraversal(TreeNode root)
{
    List<int> result = new List<int>();
    PostOrder(result, root);
    return result;
}
public void PostOrder(List<int> result, TreeNode node)
{
    if (node == null) return;
    PostOrder(result, node.left);//左
    PostOrder(result, node.right);//右
    result.Add(node.val);//中
}

迭代遍历

前序遍历

/// <summary>
/// 前序遍历（中左右）
/// </summary>
/// <param name="root"></param>
/// <returns></returns>
public IList<int> PreOrderTraversal(TreeNode root)
{
    IList<int> res = new List<int>();
    Stack<TreeNode> st = new Stack<TreeNode>();
    if (root != null) st.Push(root);
    while (st.Count > 0)
    {
        TreeNode node = st.Pop();
        if (node != null)
        {
            if (node.right != null) st.Push(node.right);
            if (node.left != null) st.Push(node.left);
            st.Push(node);
            st.Push(null);
        }
        else
        {
            node = st.Pop();
            res.Add(node.val);
        }
    }
    return res;
}

中序遍历

/// <summary>
/// 中序遍历（左中右）
/// </summary>
/// <param name="root"></param>
/// <returns></returns>
public IList<int> InorderTraversal(TreeNode root)
{
    IList<int> res = new List<int>();
    Stack<TreeNode> st = new Stack<TreeNode>();
    if (root != null) st.Push(root);
    while (st.Count > 0)
    {
        TreeNode node = st.Pop();
        if (node != null)
        {
            if (node.right != null) st.Push(node.right);
            st.Push(node);
            st.Push(null);
            if (node.left != null) st.Push(node.left);
        }
        else
        {
            node = st.Pop();
            res.Add(node.val);
        }
    }
    return res;
}

后续遍历

/// <summary>
/// 后序遍历（左右中）
/// </summary>
/// <param name="root"></param>
/// <returns></returns>
public IList<int> PostOrderTraversal(TreeNode root)
{
    IList<int> res = new List<int>();
    Stack<TreeNode> st = new Stack<TreeNode>();
    if (root != null) st.Push(root);
    while (st.Count > 0)
    {
        TreeNode node = st.Pop();
        if (node != null)
        {
            st.Push(node);
            st.Push(null);
            if (node.right != null) st.Push(node.right);
            if (node.left != null) st.Push(node.left);
        }
        else
        {
            node = st.Pop();
            res.Add(node.val);
        }
    }
    return res;
}

层序遍历

递归遍历

IList<IList<int>> res = new List<IList<int>>();
public IList<IList<int>> LevelOrder(TreeNode root)
{
    LevelDFS(root, 0);
    return res;
}
public void LevelDFS(TreeNode root, int deep)
{
    if (root == null) return;
    deep++;
    if (res.Count < deep)
    {
        IList<int> item = new List<int>();
        res.Add(item);
    }
    res[deep - 1].Add(root.val);
    LevelDFS(root.left, deep);
    LevelDFS(root.right, deep);
}

迭代遍历

IList<IList<int>> res = new List<IList<int>>();
public IList<IList<int>> LevelOrder(TreeNode root)
{
    Queue<TreeNode> que = new Queue<TreeNode>();
    if (root != null) que.Enqueue(root);
    while (que.Count > 0)
    {
        IList<int> item = new List<int>();
        int len = que.Count;
        while (len > 0)
        {
            TreeNode node = que.Dequeue();
            item.Add(node.val);
            if (node.left != null) que.Enqueue(node.left);
            if (node.right != null) que.Enqueue(node.right);
            len--;
        }
        res.Add(item);
    }
    return res;
}

代码随想录: https://programmercarl.com