第十章 优先级队列 (xa3)左式堆:插入与删除


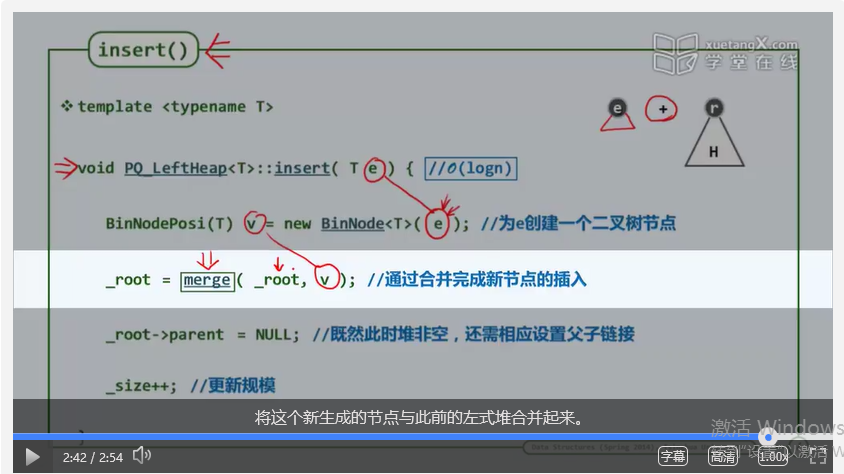

第十章 优先级队列 (xa3)左式堆:插入与删除的更多相关文章
- 第十章 优先级队列 (xa2)左式堆:合并
- 第十章 优先级队列 (xa1)左式堆:结构
- Heap:左式堆的应用例(任意序列变单调性最小价值)
首先来说一下什么是左式堆: A:左式堆是专门用来解优先队列合并的麻烦(任意二叉堆的合并都必须重新合并,O(N)的时间). 左式堆的性质: 1.定义零路经长:节点从没有两个两个儿子节点的路经长,把NUL ...
- My集合框架第六弹 左式堆
左式堆(Leftist Heaps)又称作最左堆.左倾堆.左式堆作为堆的一种,保留了堆的一些属性. 第1,左式堆仍然以二叉树的形式构建: 第2,左式堆的任意结点的值比其子树任意结点值均小(最小堆的特性 ...
- 结构之美——优先队列基本结构(四)——二叉堆、d堆、左式堆、斜堆
实现优先队列结构主要是通过堆完成,主要有:二叉堆.d堆.左式堆.斜堆.二项堆.斐波那契堆.pairing 堆等. 1. 二叉堆 1.1. 定义 完全二叉树,根最小. 存储时使用层序. 1.2. 操作 ...
- 第十章 优先级队列 (b4)完全二叉堆:批量建堆
- 第十章 优先级队列 (b3)完全二叉堆:删除与下滤
- 第十章 优先级队列 (b2)完全二叉堆:插入与上滤
- 第十章 优先级队列 (b1)完全二叉堆:结构
随机推荐
- 2. apache整合tomcat部署集群
apache只有处理静态事物的能力, 而tomcat的强项就是处理动态的请求,所以apache和tomcat整合相互取长补短,由apache作为入口,如果是请求静态页面或者是静态文件,由apache直 ...
- 1. orcle 创建可扩展表空间
1.创建表空间 a). create tablespace tablespacename datafile 'D:\tablespace\tablespacename.dbf' size 200m a ...
- 高级js--(面向对象js,arguments,闭包,自调)
1. Arguments对象 l检测参数个数 1.在函数代码中,使用特殊对象 arguments,开发者无需明确指出参数名,就能访问它们. function howManyArgs() { al ...
- vbox 按照增强工具 centos7
命令:mount -t auto /dev/cdrom /mnt/cdrom 这命令就是把CentOS CDROM挂载在/mnt/cdrom目录中,这样我们就可以访问光盘里面的内容了.执行“mount ...
- jquery循环方法
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- css-实现子元素垂直居中
1.父元素:position:relative; 2.子元素:position:absolute; top:50%; transform:translate(0,-50%); 完美解决
- 1037C_ Equalize(字符串)
modify 改变 C. Equalize time limit per test 1 second memory limit per test 256 megabytes input standar ...
- Go的50度灰:Golang新开发者要注意的陷阱和常见错误(转)
目录 [−] 初级 开大括号不能放在单独的一行 未使用的变量 未使用的Imports 简式的变量声明仅可以在函数内部使用 使用简式声明重复声明变量 偶然的变量隐藏Accidental Variable ...
- Java重写equals方法(重点讲解)
为什么equals()方法要重写? 判断两个对象在逻辑上是否相等,如根据类的成员变量来判断两个类的实例是否相等,而继承Object中的equals方法只能判断两个引用变量是否是同一个对象.这样我们往往 ...
- Linux Install redis
1.将下载好的压缩包放到/usr/local目录下# tar xzf redis-3.0.2.tar.gz # cd redis-3.0.2 # make//--------------------- ...
