【Java】 大话数据结构(15) 排序算法(2) （快速排序及其优化）

本文根据《大话数据结构》一书，实现了Java版的快速排序。

更多：数据结构与算法合集

基本概念

　　基本思想：在每轮排序中，选取一个基准元素，其他元素中比基准元素小的排到数列的一边，大的排到数列的另一边；之后对两边的数列继续进行这种排序，最终达到整体有序。

　　

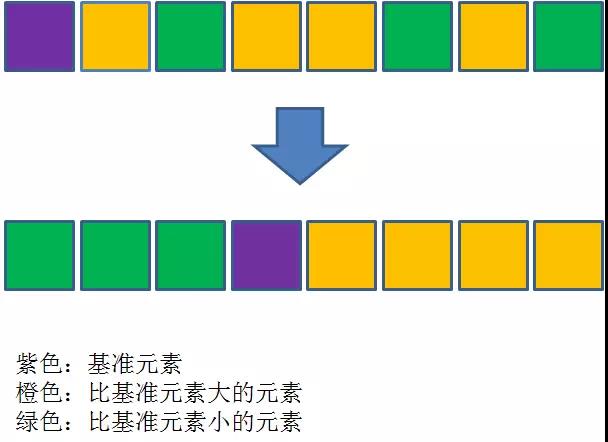
图片来自公众号：程序员小灰

实现代码

　　根据上述基本思想，可以先写出快速排序最核心的代码：对于数组a中从下标为low至下标为high的元素，选取一个基准元素（记为pivotKey），根据与基准比较的大小，将这些元素排到基准元素的两端。

　　注意点：1.两端向中间扫描时，一定要先从高段往低端扫描（low<high && a[high]<pivotKey)，这样才能实现pivotKey一直会交换到中间。!!

　　　　　　2.比较大小时不要忘记low<high还要一直成立，即（low<high && a[high]<pivotKey)。!!  例如，数组全为同一个数字时，不加这个判断有可能导致越界

	/**
	 * 对数组a中下标从low到high的元素，选取基准元素pivotKey，
	 * 根据与基准比较的大小，将各个元素排到基准元素的两端。
	 * 返回值为最后基准元素的位置
	 */
	public int partition(int[] a, int low, int high) {
		int pivotKey = a[low];	//用第一个元素作为基准元素
		while (low < high) { //两侧交替向中间扫描
			while (low < high && a[high] >= pivotKey)
				high--;
			swap(a, low, high);  //比基准小的元素放到低端
			while (low < high && a[low] <= pivotKey)
				low++;
			swap(a, low, high);  //比基准大的元素放到高端
		}
		return low;		//返回基准元素所在位置
	}

　　将元素分为两部分后，必须对两个子部分继续进行上面的排序，所以要用到递归。代码如下：

	/**
	 * 递归调用
	 */
	public void qSort(int[] a, int low, int high) {
		int pivot;
		if (low >= high)
			return;
		pivot = partition(a, low, high);  //将数列一分为二
		qSort(a, low, pivot - 1);	//对低子表排序
		qSort(a, pivot + 1, high);	//对高子表排序
	}

　　

完整Java代码

（含测试代码）

import java.util.Arrays;

/**
 *
 * @Description 快速排序
 *
 * @author yongh
 * @date 2018年9月14日 下午2:39:00
 */
public class QuickSort {
	public void quickSort(int[] a) {
		if (a == null)
			return;
		qSort(a, 0, a.length - 1);
	}

	/**
	 * 递归调用
	 */
	public void qSort(int[] a, int low, int high) {
		int pivot;
		if (low >= high)
			return;
		pivot = partition(a, low, high);  //将数列一分为二
		qSort(a, low, pivot - 1);	//对低子表排序
		qSort(a, pivot + 1, high);	//对高子表排序
	}

	/**
	 * 对数组a中下标从low到high的元素，选取基准元素pivotKey，
	 * 根据与基准比较的大小，将各个元素排到基准元素的两端。
	 * 返回值为最后基准元素的位置
	 */
	public int partition(int[] a, int low, int high) {
		int pivotKey = a[low];	//用第一个元素作为基准元素
		while (low < high) { //两侧交替向中间扫描
			while (low < high && a[high] >= pivotKey)
				high--;
			swap(a, low, high);  //比基准小的元素放到低端
			while (low < high && a[low] <= pivotKey)
				low++;
			swap(a, low, high);  //比基准大的元素放到高端
		}
		return low;		//返回基准元素所在位置
	}

	public void swap(int[] a, int i, int j) {
		int temp;
		temp = a[j];
		a[j] = a[i];
		a[i] = temp;
	}

	// =========测试代码=======
	public void test1() {
		int[] a = null;
		quickSort(a);
		System.out.println(Arrays.toString(a));
	}

	public void test2() {
		int[] a = {};
		quickSort(a);
		System.out.println(Arrays.toString(a));
	}

	public void test3() {
		int[] a = { 1 };
		quickSort(a);
		System.out.println(Arrays.toString(a));
	}

	public void test4() {
		int[] a = { 3, 3, 3, 3, 3 };
		quickSort(a);
		System.out.println(Arrays.toString(a));
	}

	public void test5() {
		int[] a = { -3, 6, 3, 1, 3, 7, 5, 6, 2 };
		quickSort(a);
		System.out.println(Arrays.toString(a));
	}

	public static void main(String[] args) {
		QuickSort demo = new QuickSort();
		demo.test1();
		demo.test2();
		demo.test3();
		demo.test4();
		demo.test5();
	}
}

　　

null
[]
[]
[, , , , ]
[-, , , , , , , , ]

QuickSort

快速排序优化

　1.优化选取枢纽

　　基准应尽量处于序列中间位置，可以采取“三数取中”的方法，在partition()方法开头加以下代码，使得a[low]为三数的中间值：

		// 三数取中,将中间元素放在第一个位置
		if (a[low] > a[high])
			swap(a, low, high);
		if (a[(low + high) / 2] > a[high])
			swap(a, (low + high) / 2, high);
		if (a[low] < a[(low + high) / 2])
			swap(a, (low + high) / 2, low);

　　

　2.优化不必要的交换

　　两侧向中间扫描时，可以将交换数据变为替换：

		while (low < high) { // 两侧交替向中间扫描
			while (low < high && a[high] >= pivotKey)
				high--;
			a[low] = a[high];
			// swap(a, low, high); //比基准小的元素放到低端
			while (low < high && a[low] <= pivotKey)
				low++;
			a[high] = a[low];
			// swap(a, low, high); //比基准大的元素放到高端
		}
		a[low]=pivotKey;  //在中间位置放回基准值

　　

　3.优化小数组时的排序方案

　　当数组非常小时，采用直接插入排序（简单排序中性能最好的方法）

　4.优化递归操作

　　qSort()方法中，有两次递归操作，递归对性能有较大影响。因此，使用while循环，在第一次递归后，变量low就没有用处了，可将pivot+1赋值给low，下次循环中，partition(a, low, high)的效果等同于qSort(a, pivot + 1, high)，从而可以减小堆栈的深度，提高性能。

		// pivot = partition(a, low, high); // 将数列一分为二
		// qSort(a, low, pivot - 1); // 对低子表排序
		// qSort(a, pivot + 1, high); // 对高子表排序

		//优化递归操作
		while (low < high) {
			pivot = partition(a, low, high); // 将数列一分为二
			qSort(a, low, pivot - 1); // 对低子表排序
			low = pivot + 1;
		}

　　

复杂度分析

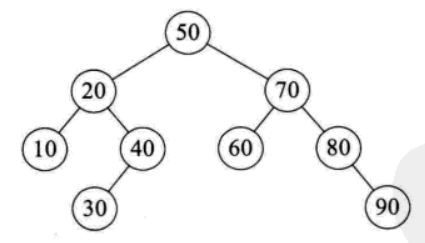
　　快速排序时间性能取决于递归深度，而空间复杂度是由递归造成的栈空间的使用。递归的深度可以用递归树来描述，如{50，10，90，30，70，40，80，60，20}的递归树如下：

　最优情况：

　　最优情况下，每次选取的基准元素都是元素中间值，partition()方法划分均匀，此时根据二叉树的性质4可以知道，排序n个元素，其递归树的深度为[log₂n]+1，所以仅需要递归log₂n次。

　　将排序n个元素的时间记为T(n)，则有以下推断：

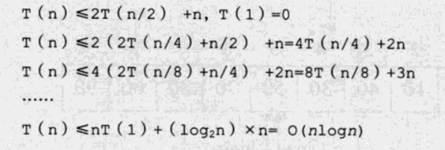
　　所以最优情况下的时间复杂度为：O(nlogn)；同样根据递归树的深度，最优空间复杂度为O(logn)。

　最坏情况：

　　递归树为一棵斜树，需要n-1次调用，所以最坏空间复杂度为O(logn)。在第i次调用中需要n-1次的关键字比较，所以比较次数为：Σ(n-i)=(n-1)+……+2+1=n(n-1)/2，所以最坏时间复杂度为O(n^2）。

　平均情况：

　　

　　平均时间复杂度：O(nlogn)，平均空间复杂度O(logn)。

更多：数据结构与算法合集