python 回溯法 子集树模板 系列 —— 6、排课问题

问题

某乡村小学有六个年级，每个年级有一个班，共六个班。

周一到周五，每天上6节课，共计30节课。

开设的课程

一年级：语(9)数(9)书(2)体(2)美(2)音(2)德(2)班(1)安(1)

二年级：语(9)数(9)书(2)体(2)美(2)音(2)德(2)班(1)安(1)

三年级：语(8)数(8)英(4)体(2)美(2)音(2)德(2)班(1)安(1)

四年级：语(8)数(8)英(4)体(2)美(2)音(2)德(2)班(1)安(1)

五年级：语(8)数(8)英(4)体(2)美(2)音(2)德(2)班(1)安(1)

六年级：语(8)数(8)英(4)体(2)美(2)音(2)德(2)班(1)安(1)

要求

• 各门课课时必须相符
• 周一最后一节课班会，周五最后一节课安全教育是固定的。
• 上午只能排语、数、英
• 全校只有两位音乐老师
• 三年级的数学不能排在周五上午第三节（三年级数学潘老师家里有事）

分析

将每一个（时间，空间）点对，作为一个元素。这些元素都具有各自的[状态1，状态2，状态3，状态4，状态5，状态6，状态7，状态8，状态9]共9个状态。

（时间，空间） --> 状态

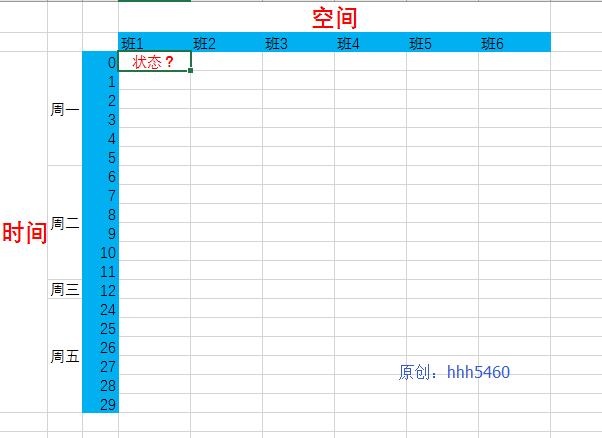
一种状态对应一个课程。

对每一个元素，遍历相应的9种状态。

解的长度是固定的，30 * 6 的二维数组

套用子集树模板即可。

本问题只需要解决存在性。也就是说，只要找到一个符合要求的解就ok了。

此问题的本质就是，各(时,空)点对的取各自状态搭配的问题。

代码

'''排课问题'''

# 作者：hhh5460
# 写于：2017年5月30日22时33分
# 声明：此算法的版权归本人所有

m = 30  # 一周课时数（时间）
n = 6   # 全校班级数（空间）
o = 30 * 6  # 元素个数，即(时, 空)点对的个数

# 6个班开始的课程（状态空间）
a = [['语','数','书','体','美','音','德','班','安'], # 一年级
     ['语','数','书','体','美','音','德','班','安'], # 二年级
     ['语','数','英','体','美','音','德','班','安'], # 三年级
     ['语','数','英','体','美','音','德','班','安'], # 四年级
     ['语','数','英','体','美','音','德','班','安'], # 五年级
     ['语','数','英','体','美','音','德','班','安']] # 六年级

# 课时数
b = [[9,9,2,2,2,2,2,1,1],
     [9,9,2,2,2,2,2,1,1],
     [8,8,4,2,2,2,2,1,1],
     [8,8,4,2,2,2,2,1,1],
     [8,8,4,2,2,2,2,1,1],
     [8,8,4,2,2,2,2,1,1]]

x = [[0 for _ in range(n)] for _ in range(m)] # 一个解，m*n 的二维数组

is_found = False  # 结束所有递归标志!!!!!

# 冲突检测
def conflict(t, s):
    '''只考虑刚刚排的x[t][s]'''

    global m,n,o,a,b,x

    # 一、各门课课时数必须相符（纵向看）
    # 1.前面已经排的课时不能超
    if [r[s] for r in x[:t+1]].count(x[t][s]) > b[s][a[s].index(x[t][s])]: # 黑科技，不要眼花！
        return True
    # 2.后面剩的课时不能不够
    if [r[s] for r in x[:t+1]].count(x[t][s]) + (m-t-1) < b[s][a[s].index(x[t][s])]:
        return True

    # 二、周一最后一节课班会，周五最后一节课安全教育是固定的。
    # 1.周一最后一节课班会
    if x[t][s] == '班' and t != 5:
        return True
    # 2.周五最后一节课安全教育
    if x[t][s] == '安' and t != 29:
        return True

    # 三、上午只能排语、数、英
    if t % 6 in [0,1,2] and x[t][s] not in ['语','数','英']:
        return True

    # 四、只有两个音乐老师（横向看）
    # 前面已经排的班级不能有3个及以上的班级同时上音乐课
    if x[t][s] == '音' and x[t][:s+1].count('音') >= 3:
        return True

    # 五、三年级的数学不能排在周五上午第三节（三年级数学潘老师家里有事）
    if x[t][s] == '数' and t==5*n+3-1:
        return True

    return False # 无冲突

# 套用子集树模板
def paike(t, s): # 到达(t,s)时空点对的位置
    global m,n,o,a,b,x, is_found

    if is_found: return # 结束所有递归

    if t == m:  # 超出最尾的元素
        #print(x)
        show(x) # 美化版
        is_found = True # 只需找一个
    else:
        for i in a[s]: # 遍历第s个班级的对应的所有状态，不同的班级状态不同
            x[t][s] = i
            if not conflict(t, s): # 剪枝
                ns = [s + 1, 0][s + 1 == n] # 行扫描方式
                nt = [t, t + 1][s + 1 == n]
                paike(nt, ns) # 去往(nt, ns)时空点对

# 可视化一个解x
def show(x):
    import pprint

    pprint.pprint(x[:6])    # 全校的周一课表
    pprint.pprint(x[6:12])  # 全校的周二课表
    pprint.pprint(x[12:18]) # 全校的周三课表
    pprint.pprint(x[18:24]) # 全校的周四课表
    pprint.pprint(x[24:])   # 全校的周五课表

# 测试
paike(0, 0) # 从时空点对(0,0)开始

效果图

正在运行中... ... 稍后奉上。

补：现在时间2017年6月1日7时40分，程序已运行34+时，还没有结果，囧！

之所以这么慢，其原因可能是递归太多了！

好吧，那只能等我以后将递归版本改为迭代版本，再运行看其结果如何了。