笛卡尔遗传规划Cartesian Genetic Programming (CGP)简单理解(1)

初识遗传算法Genetic Algorithm(GA)

　　遗传算法是计算数学中用于解决最优化的搜索算法，是进化算法的一种。进化算法借鉴了进化生物学中的一些现象而发展起来的，这些现象包括遗传、突变、自然选择以及杂交等，是一个通过计算机模拟解决最优化问题的过程，遗传算法从代表问题可能存在的一个解集的一个种群(population)开始的,一个种群由一定数量的候选解也称为个体(individual)组成，个体由基因(gene)编码而成，基因的表现形式实际上是每个个体上带有的染色体(chromosome) 染色体即为基因的集合，应用遗传算法的一般步骤是：1.需要实现表现形到基因型的编码工作，常用编码方法有二进制编码、格雷码编码、浮点编码和符号编码。2.进化从随机个体(初代种群)的种群开始，之后一代一代进化。按照优胜劣汰的准则在每一代中，评价整个种群的适应度(fitness)，从当前种群中选择(selection)多个个体(基于它们的适应度)。3.借助于自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)和变异(mutation) 产生新的种群，该种群在算法的下一次迭代中成为新的种群。4.在末代种群中的最优个体通过解码(decoding)产生最优解

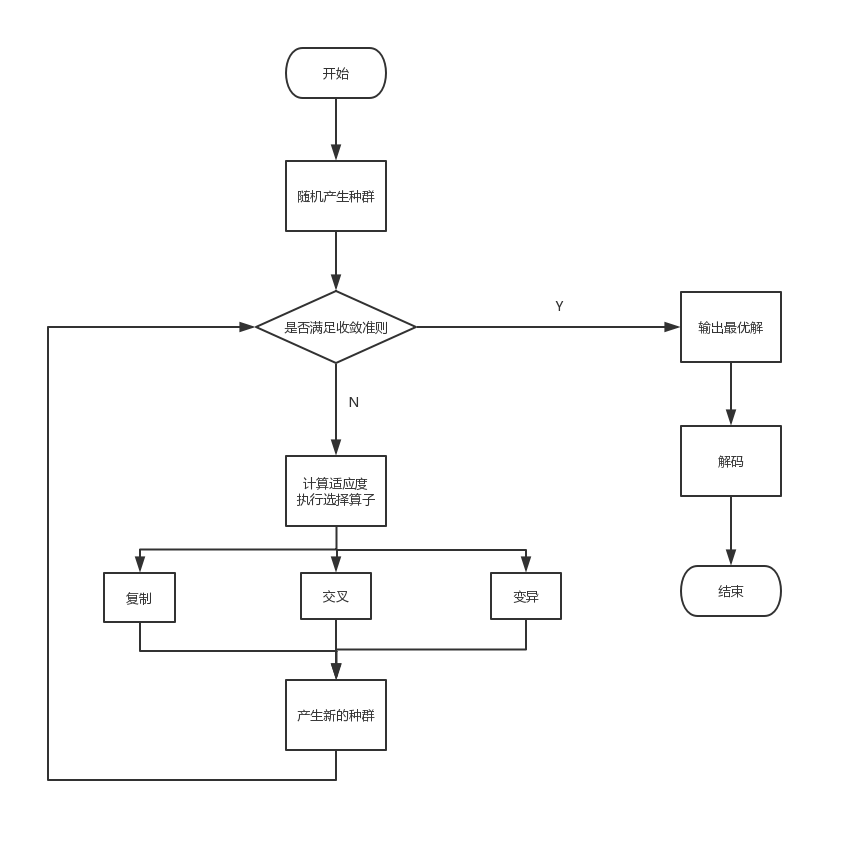
笛卡尔遗传规划介绍

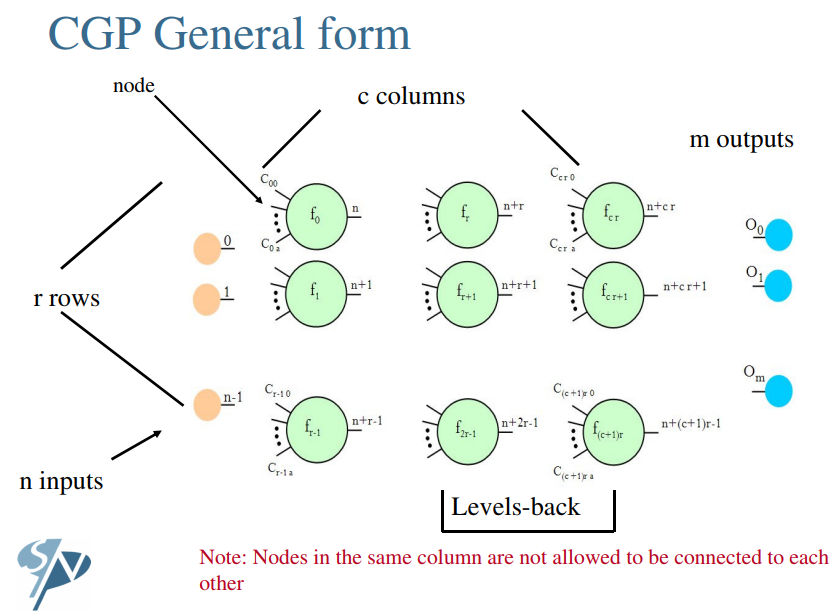
　　笛卡尔遗传规划源自 Miller 等人对进化数字电路的发展。1999 年出现了专门研究笛卡尔遗传规划的团队2000 年由 Miller 等人发表了Cartesian Genetic Programming，正式提出了笛卡尔遗传规划的一般形式。笛卡尔遗传规划由一个带索引节点的有向图表示，这是一个有n个输入m个输出的有向图(directed graph)，其中输入节点的下标为 0 到 n-1，输出由最后一列的m个节点得到。有向图的每个节点都由 4 个正整数组成，其中包含 2 个输入位、1 个参数位和 1 个用来索引使用函数的函数索引位。每个节点通过两个输入、一个参数并通过所选函数计算出节点的输出。如图所示该个体的染色体的基因型由这些节点组成，有向图的大小为\(r\times c\),其中同一列的节点不可以互相连接，节点只能向前连接，不同列的节点的连接限制为Levels-back(例如Levels-back = 2 那么第i列的节点最多可以连接到i-2列)。不同个体之间可以交叉、变异等一系列遗传变换产生新的个体。

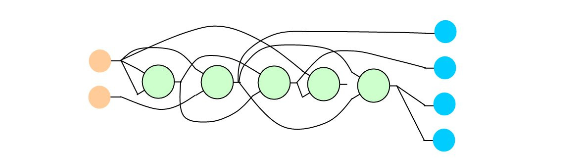
通常选用具有一行任意列的纵深形式的CGP网络，一般来说节点函数的元数一般与节点输入个数相同

Reference:

[1] Miller, Julian F. "Cartesian genetic programming." Cartesian Genetic Programming. Springer, Berlin, Heidelberg, 2011. 17-34. Online Tutorials:PPSN 2014 Tutorial

未完待续。。。。。。。