bzoj2817[ZJOI2012]波浪

题目链接：

http://www.lydsy.com/JudgeOnline/problem.php?id=2817

波浪
【问题描述】
阿米巴和小强是好朋友。 阿米巴和小强在大海旁边看海水的波涛。小强第一次面对如此汹涌的海潮， 他兴奋地叫个不停。而阿米巴则很淡定，他回想起曾经的那些日子，事业的起伏， 情感的挫折……总之今天的风浪和曾经经历的那些风雨比起来，简直什么都不 算。 于是，这对好朋友不可避免地产生了分歧。为了论证自己的观点，小强建立 了一个模型。他海面抽象成一个 1 到N的排列P[1…N]。定义波动强度等于 相邻 两项的差的绝对值的和 ，即： L = | P2 – P1 | + | P3 – P2 | + … + | PN – PN-1 | 给你一个N和M，问：随机一个 1…N的排列，它的波动强度 不小于 M的概率 有多大？ 答案请保留 小数点后 K 位输出，四舍五入 。
【输入格式】
输入文件 wavel.in 的第一行包含三个整数 N, M 和 K，分别表示排列的长度， 波动强度，输出位数。
【输出格式】
输出文件 wavel.out 包含一个小数点后 K 位的实数。
【样例输入】
3 3 3
【样例输出】
0.667
【样例说明】
N = 3 的排列有 6 个：123，132，213，231，312，321；他们的波动强度分 别为 2，3，3，3，3，2。所以，波动强度不小于 3 的概率是 4/6，即 0.667。 你也可以通过下面的代码来验证这个概率： int a[3]={0,1,2},s=0,n=3; for (int i=0;i<1000000;i++){  random_shuffle(a,a+n);  int t=0;  for (int j=0;j<n-1;j++) t+=abs(a[j+1]-a[j]); 
 if (t>=3) s++; } printf("%.3f\n",s/1000000.0);
 
【数据规模】
对于 30%的数据，N ≤ 10。 对于另外 30%的数据，K ≤ 3。 对于另外 30%的数据，K ≤ 8。 对于另外 10%的数据，N ≤ 50。 对于 100%的数据，N ≤ 100，K ≤ 30，0 ≤ M ≤ 2147483647。

题解

啊。。

我从未写过如此**的题目啊T^T

这种题估计也就fhq出的出来。。

从此我对小强和阿米巴产生了心理阴影。。

网上好像没多少题解啊。。那我再发个良心题解吧。。

好的现在开始正文。。

首先考虑从小到大在序列中插入每个数字。

比如。。

涂黑的格子表示已经放了数字的位置，然后。。我们现在要再放一个数字。

显然易见。。涂黑的格子的数字都比当前数字小

然后有这几种情况

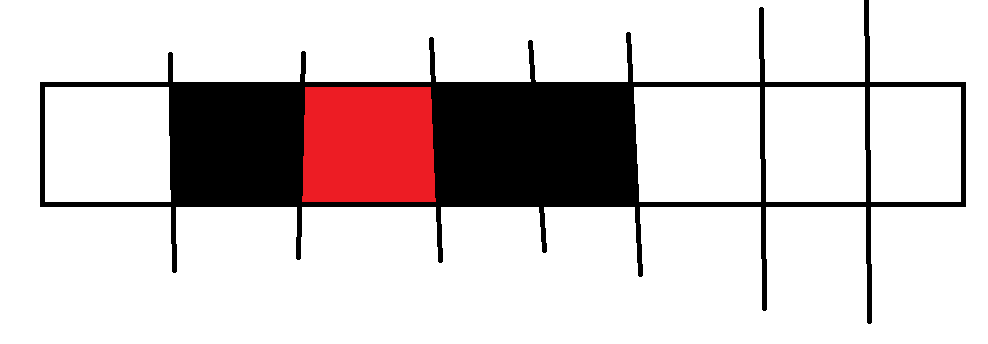
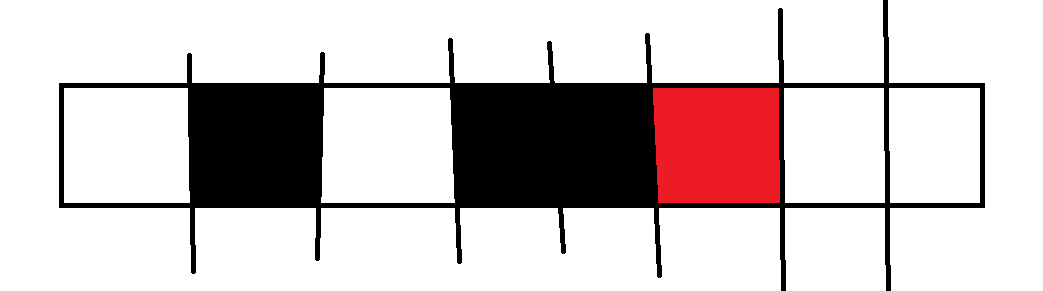
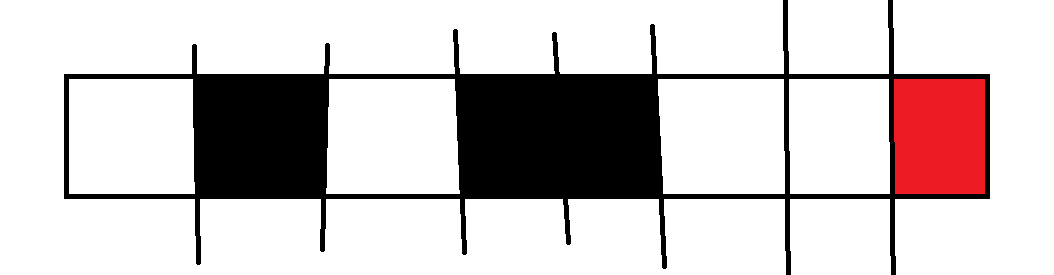
红色格子表示当前填的数字

先看第一张图，新添的格子产生了新的一段！

而且，这一段两端的数还没填。。说明，当前位置贡献的权值要-2*i（假设i为当前填的数字），因为两端的数都比这个大，又因为你有(k+1)段可以插入新的一段，所以转移系数为(k+1)。。

再看第二张图，i合并了原来的两段，说明i两端的数字都填好了，这代表着当前位置贡献的权值为2*i，因为两端的数字都比这个小,又因为你有(k-1)段可以合并两个段，多已转移系数为(k-1)。。

发现了没？我们可以DP了！

设f[i][j][k][t]表示当前插入到第i个数字，权值和为j，有k段，t。。t表示整个序列两端的情况。比如t=0表示这个序列两端都没有放数字，1表示放了一个，2表示放了两个。

然后，我们可以对第一张图列出方程：f[i][j-2*i][k+1][0]+=f[i-1][j][k][0]*(k+1)

同理，可以对第二段建立转移方程：f[i][j+2*i][k-1][0]+=f[i-1][j][k][0]*(k-1)

第三张图就是f[i][j][k][0]+=f[i-1][j][k][0]*2*k

然后第四张图，出现了边界的情况，也依然可以DP。

1、当前放在边界上的数字和别的段合成了新的一段，那么i的贡献就是i，由于有两个端点，所以转移系数是2，即方程为:f[i][j+i][k][1]+=f[i-1][j][k][0]*2

2、当前放在边界上的数字创造了新的一段，那么i的贡献就是-i，由于有两个端点，所以转移系数是2，即方程为:f[i][j-i][k+1][1]+=f[i-1][j][k][0]*2

-----------------------------------------------------------------------------以上是t=0的情况。。t=1的情况也类似，只不过。。由于你能放的位置会减少。。所以转移系数也会改变。。具体看代码。----------------------------------------------------

对了，当t=2时，就不用考虑边界情况了！

好的大体内容讲完了！

但是

但是

但是

精度30位会炸啊！！！！！

这时神器来了:__float128

优点：精度高

缺点：速度慢速度慢速度慢速度慢速度慢速度慢速度慢速度慢速度慢空间大空间大空间大空间大空间大空间大空间大空间大

又由于出题人****卡内存卡时限。。

你会发现这个代码T了。。

 #include <bits/stdc++.h>
 #define MAX 4500
 #define N 110
 using namespace std;
 typedef long long ll;
 double f[][MAX*+][N][];
 int i,j,k,n,m,x,y,t,q,la,no;
 void print2(__float128 x,int k){
     for (i=;i<=n;i++)x=x/(__float128)i;
     ll a=x;x-=a;int s[],l,j=;s[]=;
     while (a)s[++s[]]=a%,a/=;if (!s[])s[++s[]]=;l=s[];
     for (i=;i<=k+;i++){x*=;a=(int)x;x-=a;s[++s[]]=a;}
     if (s[s[]]>=)j=;int p=s[];
     while (j&&p){s[p-]++;j=s[p-]/;s[p-]%=;p--;}
     if (j){for (i=s[];i>;i--)s[i]=s[i-];s[]=;}
     putchar(''+s[]);if (k)putchar('.');for (i=;i<=k+;i++)putchar(s[i]+'');
     return;
 }
 inline void solve(int n,int m,int q){
     f[][MAX-*][][]=;f[][MAX-][][]=;f[][MAX][][]=;no=;la=;
     for (i=;i<=n;i++){
         no=-no,la=-la;
         memset(f[no],,sizeof f[no]);
         for (j=;j<=MAX*;j++)
             for (k=;k<=n-;k++){
                 if (f[la][j][k][]){
                     if (j>=*i)f[no][j-*i][k+][]+=f[la][j][k][]*(k+);
                     if (j+*i<=MAX*)f[no][j+*i][k-][]+=f[la][j][k][]*(k-);
                     f[no][j][k][]+=f[la][j][k][]*k*;
                     if (j+i<=MAX*)f[no][j+i][k][]+=f[la][j][k][]*;
                     if (j>=i)f[no][j-i][k+][]+=f[la][j][k][]*;
                 }
                 if (f[la][j][k][]){
                     if (j>=*i)f[no][j-*i][k+][]+=f[la][j][k][]*k;
                     if (j+*i<=MAX*)f[no][j+*i][k-][]+=f[la][j][k][]*(k-);
                     f[no][j][k][]+=f[la][j][k][]*(*k-);
                     if (j+i<=MAX*)f[no][j+i][k][]+=f[la][j][k][];
                     if (j>=i)f[no][j-i][k+][]+=f[la][j][k][];
                 }
                 if (f[la][j][k][]){
                     if (j+i*<=MAX*)f[no][j+i*][k-][]+=f[la][j][k][]*(k-);
                     if (j>=*i)f[no][j-i*][k+][]+=f[la][j][k][]*(k-);
                     f[no][j][k][]+=*f[la][j][k][]*(k-);
                 }
             }
     }
     __float128 ans=;
     for (i=m+MAX;i<=MAX*;i++)ans+=(__float128)(f[no][i][][]*1.000000000000);
     print2(ans,q);
 }
 int main(){
     scanf("%d%d%d",&n,&m,&q);
     solve(n,m,q);
     return ;
 }

TLE啊。。

555~

本机测试22s。。其中两个点9s。。

说明

bzoj太慢了！！！

bzoj太慢了！！！

bzoj太慢了！！！

bzoj太慢了！！！

bzoj太慢了！！！

bzoj太慢了！！！

bzoj太慢了！！！

bzoj太慢了！！！

这时，膜了一下别人的代码，发现好妙啊

原来可以将k<=8的用double做，k>8的用__float128做！

写个namespace。。。inline什么的。。就过了！！跑得飞快啊！

AC代码

 #include <bits/stdc++.h>
 #define N 110
 #define MAX 4500
 using namespace std;
 typedef long long ll;
 int i,j,k,n,m,x,y,t,q,la,no;
 namespace dob {typedef double db;db f[][][][];}
 namespace fl {typedef __float128 db;db f[][][][];}
 template <class T> inline
 void print2(T x,int k){
     for (i=;i<=n;i++)x=x/(T)i;
     ll a=x;x-=a;int s[],l,j=;s[]=;
     while (a)s[++s[]]=a%,a/=;if (!s[])s[++s[]]=;l=s[];
     for (i=;i<=k+;i++){x*=;a=(int)x;x-=a;s[++s[]]=a;}
     if (s[s[]]>=)j=;int p=s[];
     while (j&&p){s[p-]++;j=s[p-]/;s[p-]%=;p--;}
     if (j){for (i=s[];i>;i--)s[i]=s[i-];s[]=;}
     putchar(''+s[]);if (k)putchar('.');for (i=;i<=k+;i++)putchar(s[i]+'');
     return;
 }
 template <class T> inline
 void solve(T f[][][][]){
     f[][MAX-*][][]=;f[][MAX-][][]=;f[][MAX][][]=;no=;la=;
     for (int i=;i<=n;i++){
         no=-no,la=-la;
         memset(f[no],,sizeof f[no]);
         for (int j=;j<=MAX*;j++)
             for (int k=;k<=n-;k++){
                 if (f[la][j][k][]){
                     if (j>=*i)f[no][j-*i][k+][]+=f[la][j][k][]*(k+);
                     if (j+*i<=MAX*)f[no][j+*i][k-][]+=f[la][j][k][]*(k-);
                     f[no][j][k][]+=f[la][j][k][]*k*;
                     if (j+i<=MAX*)f[no][j+i][k][]+=f[la][j][k][]*;
                     if (j>=i)f[no][j-i][k+][]+=f[la][j][k][]*;
                 }
                 if (f[la][j][k][]){
                     if (j>=*i)f[no][j-*i][k+][]+=f[la][j][k][]*k;
                     if (j+*i<=MAX*)f[no][j+*i][k-][]+=f[la][j][k][]*(k-);
                     f[no][j][k][]+=f[la][j][k][]*(*k-);
                     if (j+i<=MAX*)f[no][j+i][k][]+=f[la][j][k][];
                     if (j>=i)f[no][j-i][k+][]+=f[la][j][k][];
                 }
                 if (f[la][j][k][]){
                     if (j+i*<=MAX*)f[no][j+i*][k-][]+=f[la][j][k][]*(k-);
                     if (j>=*i)f[no][j-i*][k+][]+=f[la][j][k][]*(k-);
                     f[no][j][k][]+=*f[la][j][k][]*(k-);
                 }
             }
     }
     T ans=;
     for (int i=m+MAX;i<=MAX*;i++)ans+=(T)f[no][i][][];
     print2(ans,q);
 }
 int main(){
     scanf("%d%d%d",&n,&m,&q);if (q<=)solve(dob::f);else solve(fl::f);
     return ;
 }

AC啦~

本机测试5s！！

飞起~

然后就是几个注意点。。

1：用滚动数组。。

2：要输出优化。。我曾分类讨论了K为1~30的所有情况。。。

3、做好卡评测的准备。。

4、为bzoj买一台好点的机子

完结？撒花！