数据结构- 串的模式匹配算法：BF和 KMP算法

Brute-Force算法的思想

1．BF(Brute-Force)算法

Brute-Force算法的基本思想是：

1) 从目标串s 的第一个字符起和模式串t的第一个字符进行比较，若相等，则继续逐个比较后续字符，否则从串s 的第二个字符起再重新和串t进行比较。

2) 依此类推，直至串t 中的每个字符依次和串s的一个连续的字符序列相等，则称模式匹配成功，此时串t的第一个字符在串s 中的位置就是t 在s中的位置，否则模式匹配不成功。

Brute-Force算法的实现

c语言实现：

// Test.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include <stdio.h>
#include "stdlib.h"
#include <iostream>
using namespace std;
//宏定义
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define MAXSTRLEN 100
typedef char SString[MAXSTRLEN + 1];
/************************************************************************/
/*
返回子串T在主串S中第pos位置之后的位置，若不存在，返回0
*/
/************************************************************************/
int BFindex(SString S, SString T, int pos)
{
if (pos <1 || pos > S[0] ) exit(ERROR);
int i = pos, j =1;
while (i<= S[0] && j <= T[0])
{
if (S[i] == T[j])
{
++i; ++j;
} else {
i = i- j+ 2;
j = 1;
}
}
if(j > T[0]) return i - T[0];
return ERROR;
}
void main(){
SString S = {13,'a','b','a','b','c','a','b','c','a','c','b','a','b'};
SString T = {5,'a','b','c','a','c'};
int pos;
pos = BFindex( S, T, 1);
cout<<"Pos:"<<pos;
}

2．KMP算法

2.1 算法思想：

每当一趟匹配过程中出现字符比较不等时，不需要回溯I指针，而是利用已经的带的“部分匹配”的结果将模式向右滑动尽可能远的一段距离后，继续进行比较。

即尽量利用已经部分匹配的结果信息，尽量让i不要回溯，加快模式串的滑动速度。

需要讨论两个问题：
①如何由当前部分匹配结果确定模式向右滑动的新比较起点k？
② 模式应该向右滑多远才是高效率的?

现在讨论一般情况:

假设主串：s: ‘s(1) s(2) s(3) ……s(n)’ ; 模式串：p: ‘p(1) p(2) p(3)…..p(m)’

现在我们假设主串第i个字符与模式串的第j(j<=m)个字符‘失配’后，主串第i个字符与模式串的第k(k<j)个字符继续比较。

此时，s(i)≠p(j)：

由此，我们得到关系式：即得到到1 到 j -1 的"部分匹配"结果:

‘P(1) P(2) P(3)…..P(j-1)’ = ’ S(i-j+1)……S(i-1)’

从而推导出k 到 j- 1位的“部分匹配”：即P的j-1～j-k＝S前i-1～i- (k -1))位

‘P(j - k + 1) …..P(j-1)’ = ’S(i-k+1)S(i-k+2)……S(i-1)’

由于s(i)≠p(j)，接下来s(i)将与p(k)继续比较，则模式串中的前(k-1)个字符的子串必须满足下列关系式，并且不可能存在 k’>k 满足下列关系式：(k<j)

有关系式：即(P的前k- 1 ~ 1位＝ S前i-1～i-(k-1) )位 ) ,：

‘P(1) P(2) P(3)…..P(k-1)’ = ’S(i-k+1)S(i-k+2)……S(i-1)’

现在我们把前面总结的关系综合一下,有：

由上，我们得到关系：

‘p(1) p(2) p(3)…..p(k-1)’ = ‘p(j - k + 1) …..p(j-1)’

反之，若模式串中满足该等式的两个子串，则当匹配过程中，主串中的第i 个字符与模式中的第j个字符等时，仅需要将模式向右滑动至模式中的第k个字符和主串中的第i个字符对齐。此时，模式中头k-1个字符的子串‘p(1) p(2) p(3)…..p(k-1)’ 必定与主串中的第i 个字符之前长度为k-1 的子串 ’s(j-k+1)s(j-k+2)……s(j-1)’相等，由此，匹配仅需要从模式中的第 k 个字符与主串中的第 i 个字符比较起继续进行。若令 next[j] = k ,则next[j] 表明当模式中第j个字符与主串中相应字符“失配”时，在模式中需要重新和主串中该字符进行的比较的位置。由此可引出模式串的next函数：

根据模式串P的规律： ‘p(1) p(2) p(3)…..p(k-1)’ = ‘p(j - k + 1) …..p(j-1)’

由当前失配位置j(已知) ，可以归纳计算新起点k的表达式。

由此定义可推出下列模式串next函数值：

模式匹配过程:

KMP算法的实现:

第一步，先把模式T所有可能的失配点j所对应的next[j]计算出来；

第二步：执行定位函数Index_kmp（与BF算法模块非常相似）

int KMPindex(SString S, SString T, int pos)
{
if (pos <1 || pos > S[0] ) exit(ERROR);
int i = pos, j =1;
while (i<= S[0] && j <= T[0])
{
if (S[i] == T[j]) {
++i; ++j;
} else {
j = next[j+1];
}
}
if(j > T[0]) return i - T[0];
return ERROR;
}

完整实现代码：

// Test.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include <stdio.h>
#include "stdlib.h"
#include <iostream>
using namespace std;
//宏定义
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define MAXSTRLEN 100
typedef char SString[MAXSTRLEN + 1];
void GetNext(SString T, int next[]);
int KMPindex(SString S, SString T, int pos);
/************************************************************************/
/*
返回子串T在主串S中第pos位置之后的位置，若不存在，返回0
*/
/************************************************************************/
int KMPindex(SString S, SString T, int pos)
{
if (pos <1 || pos > S[0] ) exit(ERROR);
int i = pos, j =1;
int next[MAXSTRLEN];
GetNext( T, next);
while (i<= S[0] && j <= T[0])
{
if (S[i] == T[j]) {
++i; ++j;
} else {
j = next[j];
}
}
if(j > T[0]) return i - T[0];
return ERROR;
}
/************************************************************************/
/* 求子串next[i]值的算法
*/
/************************************************************************/
void GetNext(SString T, int next[])
{ int j = 1, k = 0;
next[1] = 0;
while(j < T[0]){
if(k == 0 || T[j]==T[k]) {
++j; ++k; next[j] = k;
} else {
k = next[k];
}
}
}
void main(){
SString S = {13,'a','b','a','b','c','a','b','c','a','c','b','a','b'};
SString T = {5,'a','b','c','a','c'};
int pos;
pos = KMPindex( S, T, 1);
cout<<"Pos:"<<pos;
}

2.2 求串的模式值next[n]

k值仅取决于模式串本身而与相匹配的主串无关。

我们使用递推到方式求next函数：
1）由定义可知：
next[1] = 0;
2) 设 next[j] = k ,这个表面在模式串中存在下列关系：
‘P(1) ….. P(k-1)’ = ‘P(j - k + 1) ….. P(j-1)’
其中k为满足1< k <j的某个值，并且不可能存在k` > 满足:
‘P(1) ….. P(k`-1)’ = ‘P(j - k` + 1) ….. P(j-1)’
此时next[j+1] = ?可能有两种情况：
（1）若Pk = Pj，则表明在模式串中：

‘P(1) ….. P(k)’ = ‘P(j - k + 1) ….. P(j)’
并且不可能存在k` > 满足： ‘P(1) ….. P(k`)’ = ‘P(j - k` + 1) ….. P(j)’
即next[j+1] = k + 1 推到=》：

next[j+1] = next[j] + 1;

(2) 若Pk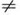Pj 则表明在模式串中：

‘P(1) ….. P(k)’ 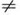‘P(j - k + 1) ….. P(j)’
此时可把next函数值的问题看成是一个模式匹配的问题，整个模式串即是主串又是模式串，
而当前匹配的过程中，已有：

Pj-k+1 = P1， Pj-k+2 = P2，... Pj-1 = Pk-1.
则当Pk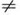Pj时应将模式向右滑动至以模式中的第next[k]个字符和主串中的第 j 个字符相比较。
若next[k] = k`,且Pj= Pk`, 则说明在主串中的第j+1 个字符之前存在一个长度为k` (即next[k])的最长子串，和模式串
从首字符其长度为看k`的子串箱等。即
‘P(1) ….. P(k`)’ = ‘P(j - k` + 1) ….. P(j)’
也就是说next[j+1] = k` +1 即
next[j+1] = next[k] + 1
同理，若Pj 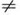Pk` ,则将模式继续向右滑动直至将模式串中的第next[k`]个字符和Pj对齐，
... ,一次类推，直至Pj和模式中某个字符匹配成功或者不存在k`(1< k` < j)满足，则:
next[j+1] =1;

/************************************************************************/
/* 求子串next[i]值的算法
*/
/************************************************************************/
void GetNext(SString T, int next[])
{ int j = 1, k = 0;
next[1] = 0;
while(j < T[0]){
if(k == 0 || T[j]==T[k]) {
++j; ++k; next[j] = k;
} else {
k = next[k];
}
}
}

next 函数值究竟是什么含义，前面说过一些，这里总结。

设在字符串S中查找模式串T，若S[m]!=T[n],那么，取T[n]的模式函数值next[n],

1. next[n] = 0 表示S[m]和T[1]间接比较过了，不相等，下一次比较 S[m+1] 和T[1]

2. next[n] =1 表示比较过程中产生了不相等，下一次比较 S[m] 和T[1]。

3. next[n] = k >1 但k<n, 表示,S[m]的前k个字符与T中的开始k个字符已经间接比较相等了，下一次比较S[m]和T[k]相等吗？

4. 其他值，不可能。

注意：

（1）k值仅取决于模式串本身而与相匹配的主串无关。

（2）k值为模式串从头向后及从j向前的两部分的最大相同子串的长度。

（3）这里的两部分子串可以有部分重叠的字符，但不可以全部重叠。

next[j]函数表征着模式P中最大相同前缀子串和后缀子串（真子串）的长度。

可见，模式中相似部分越多，则next[j]函数越大，它既表示模式T字符之间的相关度越高，也表示j位置以前与主串部分匹配的字符数越多。

即：next[j]越大，模式串向右滑动得越远，与主串进行比较的次数越少，时间复杂度就越低（时间效率）。