SHOI 2013 【扇形面积并】

早上考的，我打了80分的部分分，出来和同学讨论的时候真想扇自己一巴掌。。。。。。

题目描述：

　　

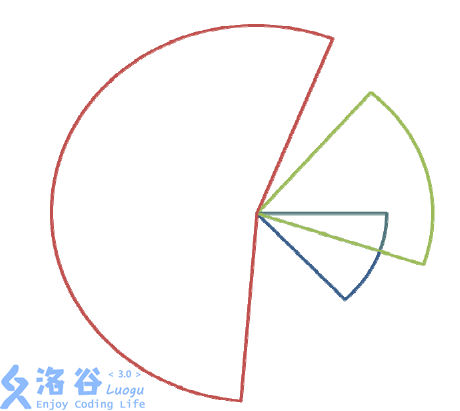
　　给定 n 个同心的扇形，求有多少面积，被至少k 个扇形所覆盖。

输入输出格式

输入格式：

第一行是三个整数 n，m，k。n 代表同心扇形个数，m代表将(−π ,π ]的角度区间平均分成2m 份。

从第二行开始的 n 行，每行三个整数r，a1，a2。描述了一个圆心在原点的扇形，半径为r，圆心角是从弧度π*a1/mπ∗a1/m到π*a2/mπ∗a2/m（a1 不一定小于 a2）。

　　输出格式：

　　　　　　输出一个整数 ans ，π/2m*ansπ/2m∗ans等于至少k 个扇形所覆盖的总面积。数据保证答案在2^{63} - 1263−1范围内。

思路分析：

嗯，好，让我们先来看看部分分做法。

30分：

　　大暴力，就不讲了吧。

60分：

　　差分，因为所有半径都是一样的，所以我们只需要求出所有被覆盖过大于等于k次的段就可以了。

80分：

　　写一棵权值线段树，在顺便用一下差分思想（在起始的地方把半径加入权值线段树，在终止的时候把半径的地方-1就好了，然后每次查找最大值）。

100分：

　　嗯，在讲100分算法前先让我扇自己一巴掌。。。。。。

　　其实你们在看80分算法的时候应该心里都在嘀咕：这不是把求最大改成求第k大不就是正解了嘛？嗯，没错，就是这样。

　　我考场脑抽了竟然没想到，啊啊啊啊啊啊啊啊啊啊啊啊！！！！！！！！！！！！！！！！！！！

代码实现：

var
    next_insert,val_insert,next_delete,val_delete:array[1..4000000]of longint;
    head_insert,head_delete:array[-1000000..1000000]of longint;
    cnt:array[-1000000..1000000]of longint;
    a:array[1..2000000]of longint;
    tot,tot_insert,tot_delete,v:longint;
    ans,x,y,n,m,need,s,t,r:int64;
    i,j:longint;
procedure add_insert(x,v:longint);
begin
    inc(tot_insert);
    next_insert[tot_insert]:=head_insert[x];
    head_insert[x]:=tot_insert;
    val_insert[tot_insert]:=v;
end;
procedure add_delete(x,v:longint);
begin
    inc(tot_delete);
    next_delete[tot_delete]:=head_delete[x];
    head_delete[x]:=tot_delete;
    val_delete[tot_delete]:=v;
end;
procedure add(s,t,r:int64);
begin
    if s=t then exit;
    inc(cnt[s]); add_insert(s,r);
    dec(cnt[t]); add_delete(t,r);
end;
procedure update(k,l,r,x,z:longint);
var
    mid:longint;
begin
    a[k]:=a[k]+z;
    if l=r then exit;
    mid:=(l+r)>>1;
    if x<=mid then update(k*2,l,mid,x,z) else update(k*2+1,mid+1,r,x,z);
end;
function query(k,l,r,need:longint):longint;
var
    mid:longint;
begin
    if l=r then exit(l);
    mid:=(l+r)>>1;
    if a[k*2+1]>=need then exit(query(k*2+1,mid+1,r,need))
    else exit(query(k*2,l,mid,need-a[k*2+1]));
end;
begin
    read(n,m,need);
    for i:=1 to n do
    begin
        read(r,s,t);　　
　　　　　　　　//是不是觉得这个读入处理很恶心，嗯，我也这么觉得。。。。。。（当我看到a1不一定小于a2时，我真想提着西瓜刀去找出题人拼命）
        if (s>=0)and(t>=0) then
        begin
            if s<t then add(s,t,r)
            else
            begin
                add(s,m,r);
                add(-m,0,r);
                add(0,t,r);
            end;
        end else
        if (s<0)and(t<0) then
        begin
            if s<t then add(s,t,r)
            else
            begin
                add(-m,t,r);
                add(0,m,r);
                add(s,0,r);
            end;
        end else
        if (s>=0)and(t<0) then
        begin
            add(s,m,r);
            add(-m,t,r);
        end else
        if (s<0)and(t>=0) then
        begin
            add(0,t,r);
            add(s,0,r);
        end;
    end;
    for i:=-m to m-1 do
    begin
        j:=head_insert[i];
        while j>0 do
        begin
            v:=val_insert[j];
            update(1,0,100000,v,1);
            j:=next_insert[j];
        end;
        j:=head_delete[i];
        while j>0 do
        begin
            v:=val_delete[j];
            update(1,0,100000,v,-1);
            j:=next_delete[j];
        end;
        x:=x+cnt[i];
        if x>=need then
        begin
            y:=query(1,0,100000,need);
            ans:=ans+sqr(y);
        end;
    end;
    writeln(ans);
end.