The League of Sequence Designers Gym - 102460E

题目链接：https://vjudge.net/problem/Gym-102460E

思路：求：

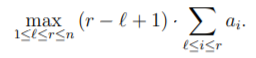
题目当中给了一段伪代码算法，仔细一看发现它是不会记录负数情况，所以与正确答案会有误差，现在题目给定K误差大小和L该数组的长度（注意L要小于2000，不然不符合上面的式子）。那么我门假设a[1]=-1，

构造l=1999,那么假算法的结果为1998*（a[2]+a[3]+...+a[n])，正确答案为1999*（a[2]+a[3]+...+a[n]-1)，因为假算法比正确答案小K，那么1998*（a[2]+a[3]+...+a[n])+K=1999*（a[2]+a[3]+...+a[n]-1);那么得到（a[2]+a[3]+...+a[n])=k+1999，只要随便构造一下a[i]就可以了。

  1 #include <bits/stdc++.h>
  2 #include <time.h>
  3 #include <set>
  4 #include <map>
  5 #include <stack>
  6 #include <cmath>
  7 #include <queue>
  8 #include <cstdio>
  9 #include <string>
 10 #include <vector>
 11 #include <cstring>
 12 #include <utility>
 13 #include <cstring>
 14 #include <iostream>
 15 #include <algorithm>
 16 #include <list>
 17 using namespace std;
 18 //cout<<setprecision(10)<<fixed;
 19 #define eps 1e-6
 20 #define PI acos(-1.0)
 21 #define lowbit(x) ((x)&(-x))
 22 #define zero(x) (((x)>0?(x):-(x))<eps)
 23 #define mem(s,n) memset(s,n,sizeof s);
 24 #define ios {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);}
 25 typedef long long ll;
 26 typedef unsigned long long ull;
 27 const int maxn=1e6+5;
 28 const ll Inf=0x7f7f7f7f7f7f7f;
 29 const ll mod=1e6+3;
 30 //const int N=3e3+5;
 31 bool isPowerOfTwo(int n) { return n > 0 && (n & (n - 1)) == 0; }//判断一个数是不是 2 的正整数次幂
 32 int modPowerOfTwo(int x, int mod) { return x & (mod - 1); }//对 2 的非负整数次幂取模
 33 int getBit(int a, int b) { return (a >> b) & 1; }// 获取 a 的第 b 位，最低位编号为 0
 34 int Max(int a, int b) { return b & ((a - b) >> 31) | a & (~(a - b) >> 31); }// 如果 a>=b,(a-b)>>31 为 0，否则为 -1
 35 int Min(int a, int b) { return a & ((a - b) >> 31) | b & (~(a - b) >> 31); }
 36 ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
 37 ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
 38 inline int read()
 39 {
 40     int X=0; bool flag=1; char ch=getchar();
 41     while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}
 42     while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}
 43     if(flag) return X;
 44     return ~(X-1);
 45 }
 46 inline void write(int X)
 47 {
 48     if(X<0) {X=~(X-1); putchar('-');}
 49     if(X>9) write(X/10);
 50     putchar(X%10+'0');
 51 }
 52 /*
 53 inline int write(int X)
 54 {
 55     if(X<0) {putchar('-'); X=~(X-1);}
 56     int s[20],top=0;
 57     while(X) {s[++top]=X%10; X/=10;}
 58     if(!top) s[++top]=0;
 59     while(top) putchar(s[top--]+'0');
 60 }
 61 */
 62 int Abs(int n) {
 63   return (n ^ (n >> 31)) - (n >> 31);
 64   /* n>>31 取得 n 的符号，若 n 为正数，n>>31 等于 0，若 n 为负数，n>>31 等于 -1
 65      若 n 为正数 n^0=n, 数不变，若 n 为负数有 n^(-1)
 66      需要计算 n 和 -1 的补码，然后进行异或运算，
 67      结果 n 变号并且为 n 的绝对值减 1，再减去 -1 就是绝对值 */
 68 }
 69 ll binpow(ll a, ll b) {
 70   ll res = 1;
 71   while (b > 0) {
 72     if (b & 1) res = res * a%mod;
 73     a = a * a%mod;
 74     b >>= 1;
 75   }
 76   return res%mod;
 77 }
 78 void extend_gcd(ll a,ll b,ll &x,ll &y)
 79 {
 80     if(b==0) {
 81         x=1,y=0;
 82         return;
 83     }
 84     extend_gcd(b,a%b,x,y);
 85     ll tmp=x;
 86     x=y;
 87     y=tmp-(a/b)*y;
 88 }
 89 ll mod_inverse(ll a,ll m)
 90 {
 91     ll x,y;
 92     extend_gcd(a,m,x,y);
 93     return (m+x%m)%m;
 94 }
 95 ll eulor(ll x)
 96 {
 97    ll cnt=x;
 98    ll ma=sqrt(x);
 99    for(int i=2;i<=ma;i++)
100    {
101     if(x%i==0) cnt=cnt/i*(i-1);
102     while(x%i==0) x/=i;
103    }
104    if(x>1) cnt=cnt/x*(x-1);
105    return cnt;
106 }
107 int t,k,l;
108 int main()
109 {
110     t=read();
111     while(t--)
112     {
113         k=read();
114         l=read();
115         if(l>=2000) {puts("-1");continue;}
116         else
117         {
118             puts("1999");
119             printf("-1 ");
120             int s=k+1999,x=1e6;
121             for(int i=1;i<1999;i++)
122             {
123                 if(s>=x)
124                 {
125                     printf("%d ",x);
126                     s-=x;
127                 }
128                 else
129                 {
130                     printf("%d ",s);
131                     s=0;
132                 }
133             }
134         }
135     }
136     return 0;
137 }