普利姆算法(prim)
普利姆算法(prim)求最小生成树(MST)过程详解
 1
1 2
2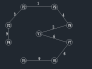 3
3 4
4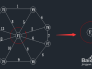 5
5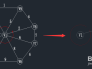 6
6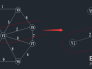 7
7
分步阅读
生活中最小生成树的应用十分广泛,比如:要连通n个城市需要n-1条边线路,那么怎么样建设才能使工程造价最小呢?可以把线路的造价看成权值求这几个城市的连通图的最小生成树。求最小造价的过程也就转化成求最小生成树的过程,则最小生成树表示使其造价最小的生成树。
那么怎么样用普利姆算法(prim算法)求最小生成树(MST)?
此以图例方式详述prim算法求最小生成树过程,希望对大家有帮助!
工具/原料
- 普利姆算法(prim算法)
- 最小生成树
一、最小生成树相关基础知识
- 1
最小生成树相关概念:
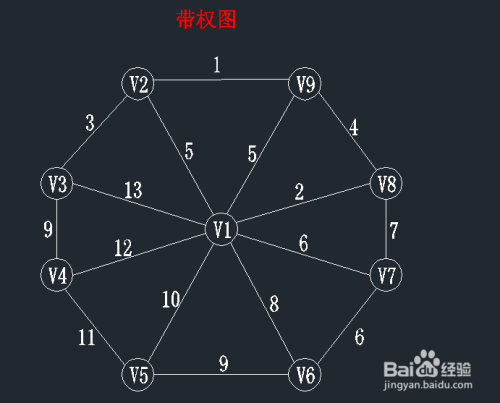
带权图:边赋以权值的图称为网或带权图,带权图的生成树也是带权的,生成树T各边的权值总和称为该树的权。
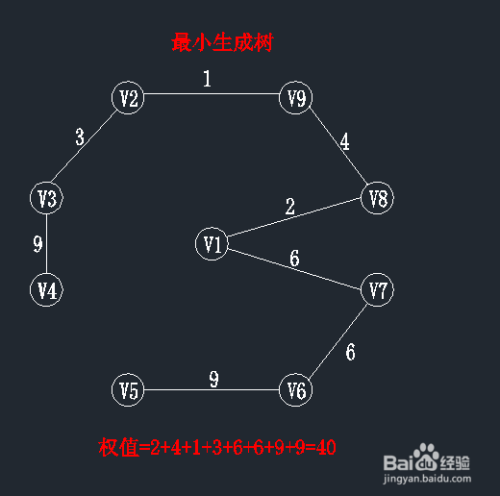
最小生成树(MST):权值最小的生成树。
生成树和最小生成树的应用:要连通n个城市需要n-1条边线路。可以把边上的权值解释为线路的造价。则最小生成树表示使其造价最小的生成树。
- 2
最小生成树的性质:
MST性质:假设G=(V,E)是一个连通网,U是顶点V的一个非空子集。若(u,v)是一条具有最小权值的边,其中u∈U,v∈V-U,则必存在一棵包含边(u,v)的最小生成树。
构造网的最小生成树必须解决下面两个问题:
(1)尽可能选取权值小的边,但不能构成回路;
(2)选取n-1条恰当的边以连通n个顶点;
 END
END
二、普利姆算法(prim算法)基本思想
- 1
prim算法基本思想:
假设G=(V,E)是连通的,TE是G上最小生成树中边的集合。算法从U={u0}(u0∈V)、TE={}开始。重复执行下列操作:
在所有u∈U,v∈V-U的边(u,v)∈E中找一条权值最小的边(u0,v0)并入集合TE中,同时v0并入U,直到V=U为止。
此时,TE中必有n-1条边,T=(V,TE)为G的最小生成树。
Prim算法的核心:始终保持TE中的边集构成一棵生成树。
看了上面一大段文字是否感觉有点晕?为了便于大家更好的理解,接下来进行算法过程的分步图解!
 END
END
三、普利姆求最小生成树算法过程图解
- 1
第一步:随意选取起点
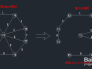
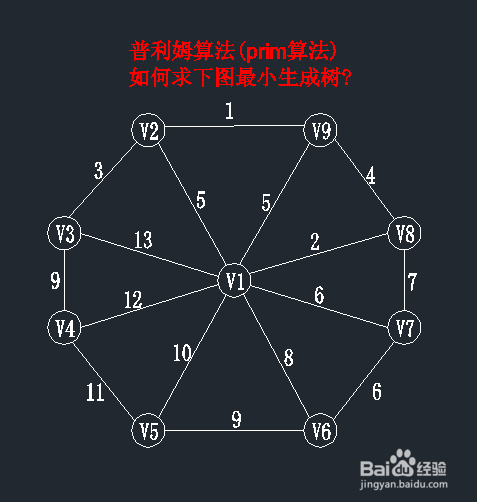
图中有9个顶点v1-v9,集合表示为:V={v1,....,V9},每条边的边权值都在图上;在进行prim算法时,我们先随意选择一个顶点作为起始点(起始点的选取不会影响最小生成树结果),在此我们一般选择v1作为起始点,现在我们设U集合为当前所找到最小生成树里面的顶点,TE集合为所找到的边。
状态如下:U={v1}; TE={};
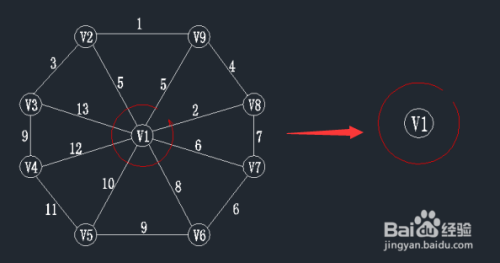
- 2
第二步:在前一步的基础上寻找最小权值
查找一个顶点在U={v1}集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v1-v8的权值最小为2,那么将v8加入到U集合,(v1,v8)加入到TE。
状态如下:U={v1,v8}; TE={(v1,v8)};
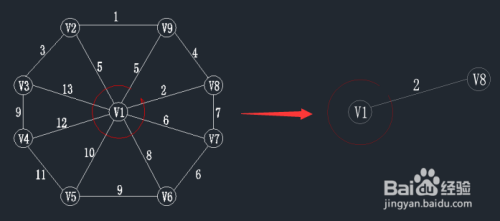
- 3
第三步:继续寻找最小权值
查找一个顶点在U={v1,v8}集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v8-v9的权值最小为4,那么将v9加入到U集合,(v8,v9)加入到TE。
状态如下:U={v1,v8,v9}; TE={(v1,v8),(v8,v9)};
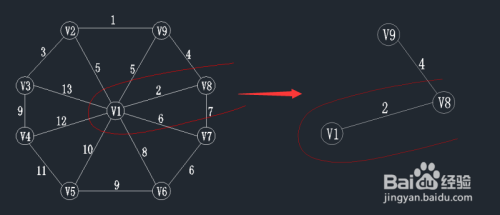
- 4
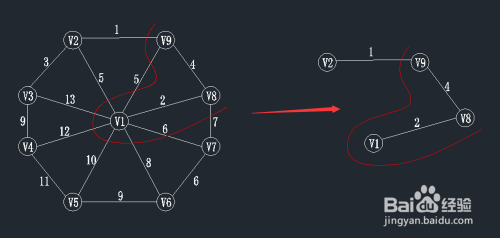
第四步:在前一步的基础上,继续寻找最小权值
查找一个顶点在U={v1,v8,v9}集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v9-v2的权值最小为1,那么将v2加入到U集合,(v9,v2)加入到TE。
状态如下:U={v1,v8,v9,v2};
TE={(v1,v8),(v8,v9),(v9,v2)};
- 5
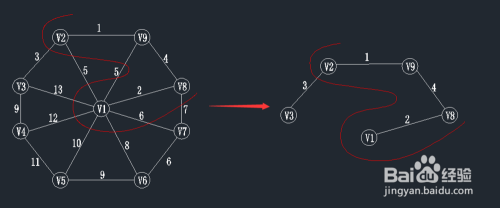
第五步:继续在前一步的基础上,寻找最小权值
查找一个顶点在U={v1,v8,v9,v2}集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v2-v3的权值最小为3,那么将v3加入到U集合,(v2,v3)加入到TE。
状态如下:U={v1,v8,v9,v2,v3};
TE={(v1,v8),(v8,v9),(v9,v2),(v2,v3)};
- 6
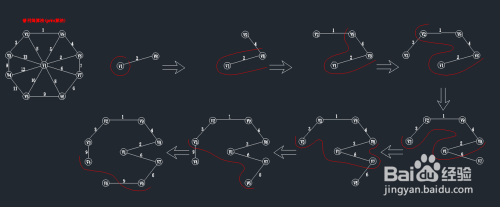
第五~九步:继续在前一步的基础上,寻找最小权值
如此循环一下直到找到所有顶点为止。到这大家应该对普利姆算法求解最小生成树的过程有所知晓,但需注意以下三点:
(1)每次都选取权值最小的边,但不能构成回路,构成环路的边则舍弃。如图中的(v1,v9),(v1,v2)等构成回路舍弃
(2)遇到权值相等,又均不构成回路的边,随意选择哪一条,均不影响生成树结果。如图中的(v3,v4),(v6,v5)权值均为9,选择哪一条在先均不影响最小生成树的生成结果。
(3)选取n-1条恰当的边以连通n个顶点。
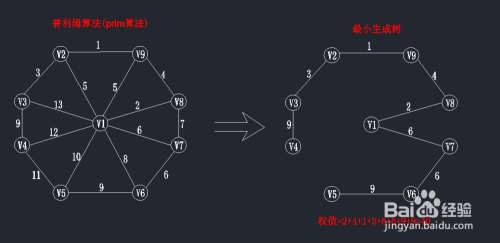
完整的算法步骤如图所示:
 END
END
四、小结
- 1
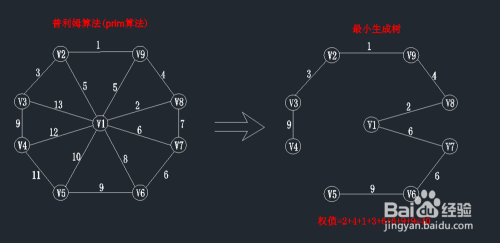
(1)最小生成树(MST)是指权值最小的生成树。
(2)prim算法是求最小生成树的算法之一,其他算法还有kruskal算法
(3)其时间复杂度为O(n^2),与边得数目无关。prim算法适合稠密图。
 END
END
注意事项
- (1)每次都选取权值最小的边,但不能构成回路,构成环路的边则舍弃。
- (2)遇到权值相等,又均不构成回路的边,随意选择哪一条,均不影响生成树结果
- (3)选取n-1条恰当的边以连通n个顶点
普利姆算法(prim)的更多相关文章
- c/c++ 用普利姆(prim)算法构造最小生成树
c/c++ 用普利姆(prim)算法构造最小生成树 最小生成树(Minimum Cost Spanning Tree)的概念: 假设要在n个城市之间建立公路,则连通n个城市只需要n-1条线路.这时 ...
- 最小生成树-普利姆算法eager实现
算法描述 在普利姆算法的lazy实现中,参考:普利姆算法的lazy实现 我们现在来考虑这样一个问题: 我们将所有的边都加入了优先队列,但事实上,我们真的需要所有的边吗? 我们再回到普利姆算法的lazy ...
- 最小生成树-普利姆算法lazy实现
算法描述 lazy普利姆算法的步骤: 1.从源点s出发,遍历它的邻接表s.Adj,将所有邻接的边(crossing edges)加入优先队列Q: 2.从Q出队最轻边,将此边加入MST. 3.考察此边的 ...
- 最小生成树练习3(普里姆算法Prim)
风萧萧兮易水寒,壮士要去敲代码.本女子开学后再敲了.. poj1258 Agri-Net(最小生成树)水题. #include<cstdio> #include<cstring> ...
- 最小生成树-普利姆(Prim)算法
最小生成树-普利姆(Prim)算法 最小生成树 概念:将给出的所有点连接起来(即从一个点可到任意一个点),且连接路径之和最小的图叫最小生成树.最小生成树属于一种树形结构(树形结构是一种特殊的图),或者 ...
- 图论---最小生成树----普利姆(Prim)算法
普利姆(Prim)算法 1. 最小生成树(又名:最小权重生成树) 概念:将给出的所有点连接起来(即从一个点可到任意一个点),且连接路径之和最小的图叫最小生成树.最小生成树属于一种树形结构(树形结构是一 ...
- HDU 1879 继续畅通工程 (Prim(普里姆算法)+Kruskal(克鲁斯卡尔))
继续畅通工程 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Sub ...
- 算法与数据结构(五) 普利姆与克鲁斯卡尔的最小生成树(Swift版)
上篇博客我们聊了图的物理存储结构邻接矩阵和邻接链表,然后在此基础上给出了图的深度优先搜索和广度优先搜索.本篇博客就在上一篇博客的基础上进行延伸,也是关于图的.今天博客中主要介绍两种算法,都是关于最小生 ...
- POJ-2421-Constructing Roads(最小生成树 普利姆)
Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 26694 Accepted: 11720 Description The ...
随机推荐
- 封装Vue Element的dialog弹窗组件
我本没有想着说要封装一个弹窗组件,但有同行的朋友在问我,而且弹窗组件也确实在项目开发中用的比较多.思前想后,又本着样式统一且修改起来方便的原则,还是再为大家分享一个我所封装的弹窗组件吧. 其实,并不是 ...
- Python3 高级编程技巧(部分)
目录: 在列表.字典.集合中筛选数据 为元组元素命名 通过列表.元组创建字典 字典排序 寻找字典的公共键 让字典保持有序 生成器函数 yield协程 同时遍历值与下标 在列表.字典.集合中筛选数据 很 ...
- java初探(1)之防止库存为负以及防超买
在秒杀业务中,会出现当只剩一个库存时,但有多个人仍然秒杀成功,且都减库存成功,因此,在减库存,更新数据库的时候,需要在sql语句上进行判断,是否库存大于0. @Update("update ...
- MVC里面调用webservice
调用WebService报错404问题 (转载) 我想在MVC4的项目添加一个webservice文件,访问没问题,但是最后调用方法就报404错误.但是如果我全新ASP.NET 空Web应用程序 ...
- redis基础数据结构及编码方式
redis基础数据结构和编码方式 一.基础数据结构 1)简单动态字符串 2)双端链表 3)字典 4)跳跃表 5)整数集合 6)压缩列表 二.对象类型与编码 在redis的数据库中创建一个新的键值对时, ...
- basicInterpreter1.02 增加对for循环的支持
源码下载:https://files.cnblogs.com/files/heyang78/basicInterpreter102-20200531-2.rar 输入: for x= to print ...
- leetcode刷题-51N皇后
题目 n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击. 给定一个整数 n,返回所有不同的 n 皇后问题的解决方案. 每一种解法包含一个明确的 n 皇后问 ...
- kickstart半自动安装centos系统与pxe自动安装centos系统
一.kickstart半自动安装centos系统 关闭防火墙,关闭selinux,使用system-config-kickstart生成kickstart配置文件,启动xmanger-Passive ...
- oracle之三rman 备份
rman 备份 7.1 归档方式下rman备份常用语法: 7.1.1 backup 备份 1)备份全库:1.1 RMAN> backup database format='/u01/myrman ...
- [LeetCode]534. 游戏玩法分析 III(Mysql)
题目 Table: Activity +--------------+---------+ | Column Name | Type | +--------------+---------+ | pl ...
