一种基于均值不等式的Listwise损失函数

一种基于均值不等式的Listwise损失函数

1 前言

1.1 Learning to Rank 简介

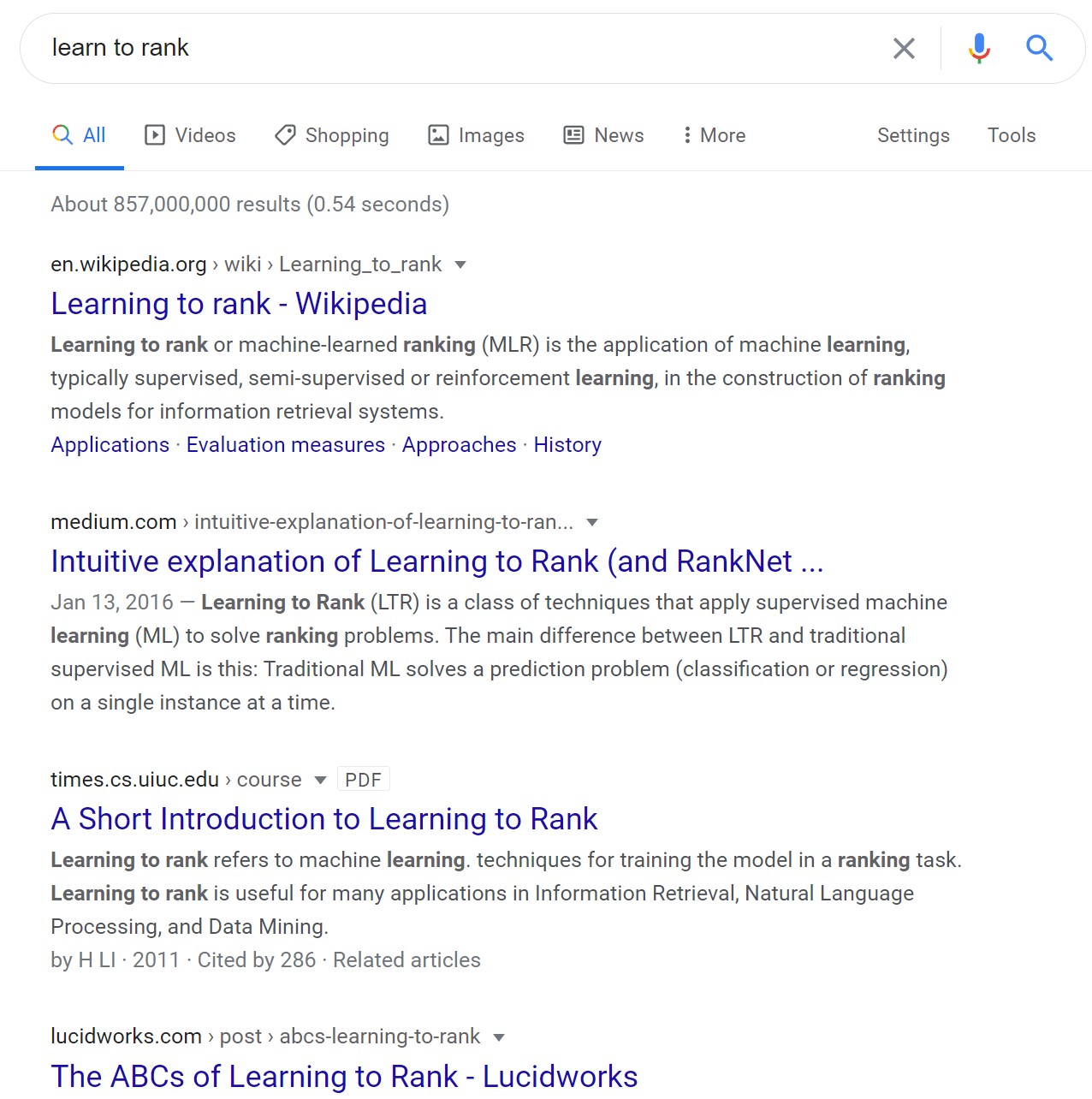
Learning to Rank (LTR) , 也被叫做排序学习, 是搜索中的重要技术, 其目的是根据候选文档和查询语句的相关性对候选文档进行排序, 或者选取topk文档. 比如在搜索引擎中, 需要根据用户问题选取最相关的搜索结果展示到首页. 下图是搜索引擎的搜索结果

1.2 LTR算法分类

根据损失函数可把LTR分为三种:

1. Pointwise, 该类型算法将LTR任务作为回归任务来训练, 即尝试训练一个为文档和查询语句的打分器, 然后根据打分进行排序.
2. Pairwise, 该类型算法的损失函数考虑了两个候选文档, 学习目标是把相关性高的文档排在前面, triplet loss 就属于Pairwise, 它的损失函数是

\[loss = max(0, score_{neg}-score_{pos}+margin)
\]

可以看出该损失函数一次考虑两个候选文档.

3. Listwise, 该类型算法的损失函数会考虑多个候选文档, 这是本文的重点, 下面会详细介绍.

1.3 本文主要内容

本文主要介绍了本人在学习研究过程中发明的一种新的Listwise损失函数, 以及该损失函数的使用效果. 如果读者对LTR任务及其算法还不够熟悉, 建议先去学习LTR相关知识, 同时本人博文自然语言处理中的负样本挖掘 (分类与排序任务中如何选择负样本) 也和本文关系较大, 可以先进行阅读.

2 预备知识

2.1 数学符号定义

\(q\)代表用户搜索问题, 比如"如何成为宇航员", \(D\)代表候选文档集合,\(d^+\)代表和\(q\)相关的文档,\(d^-\)代表和\(q\)不相关的文档, \(d^+_i\)代表第\(i\)个和\(q\)相关的文档, LTR的目标就是根据\(q\)找到最相关的文档\(d\)

2.2 学习目标

本次学习目标是训练一个打分器 scorer, 它可以衡量q和d的相关性, \(scorer(q, d)\)就是相关性分数,分值越大越相关. 当前主流方法下, scorer一般选用深度神经网络模型.

2.3训练数据分类

损失函数不同, 构造训练数据的方法也会不同:

-Pointwise, 可以构造回归数据集, 相关的数据设为1, 不相关设为0.

-Pairwise, 可构造triplet类型的数据集, 形如(\(q,d^+, d^-\))

-Listwise, 可构造这种类型的训练集: (\(q,d^+_1,d^+_2..., d^+_n , d^-_1, d^-_2, ..., d^-_{n+m}\)), 一个正例还是多个正例也会影响到损失函数的构造, 本文提出的损失函数是针对多正例多负例的情况.

3 基于均值不等式的Listwise损失函数

3.1 损失函数推导过程

在上一小结我们可以知道,训练集是如下形式 (\(q,d^+_1,d^+_2..., d^+_n , d^-_1, d^-_2, ..., d^-_{n+m}\)), 对于一个q, 有n个相关的文档和m个不相关的文档, 那么我们一共可以获取m+n个分值:\((score_1,score_2,...,score_n,...,score_{n+m})\), 我们希望打分器对相关文档打分趋近于正无穷, 对不相关文档打分趋近于负无穷.

对m+n个分值做一个softmax得到\(p_1,p_2,...,p_n,...,p_{n+m}\), 此时\(p_i\)可以看作是第i个候选文档与q相关的概率, 显然我们希望\(p_1,p_2,...,p_n\)越大越好, \(p_{n+1},...,p_{m+n}\)越小越好, 即趋近于0. 因此我们暂时的优化目标是\(\sum_{i=1}^{n}{p_i} \rightarrow 1\).

但是这个优化目标是不合理的, 假设\(p_1=1\), 其他值全为0, 虽然满足了上面的要求, 但这并不是我们想要的. 因为我们不仅希望\(\sum_{i=1}^{n}{p_i} \rightarrow 1\), 还希望相关候选文档的每一个p值都要足够大, 即我们希望: n个候选文档都与q相关的概率是最大的, 所以我们真正的优化目标是:

\[\max(\prod_{i=1}^{n}{p_i} ) , \sum_{i=1}^{n}{p_i} = 1
\]

当前情况下, 损失函数已经可以通过代码实现了, 但是我们还可以做一些化简工作, \(\prod_{i=1}^{n}{p_i}\)是存在最大值的, 根据均值不等式可得:

\[\prod_{i=1}^{n}{p_i} \leq (\frac{\sum_{i=1}^{n}{p_i}}{n})^n
\]

对两边取对数:

\[\sum_{i=1}^{n}{log(p_i)} \leq -nlog(n)
\]

这样是不是感觉清爽多了, 然后我们把它转换成损失函数的形式:

\[loss = -nlog(n) - \sum_{i=1}^{n}{log(p_i)}
\]

所以我们的训练目标就是\(\min{(loss)}\)

3.2 使用pytorch实现该损失函数

在获取到最终的损失函数后, 我们还需要用代码来实现, 实现代码如下:

# A simple example for my listwise loss function
# Assuming that n=3, m=4
# In[1]
# scores
scores = torch.tensor([[3,4.3,5.3,0.5,0.25,0.25,1]])
print(scores)
print(scores.shape)
'''
tensor([[0.3000, 0.3000, 0.3000, 0.0250, 0.0250, 0.0250, 0.0250]])
torch.Size([1, 7])
'''
# In[2]
# log softmax
log_prob = torch.nn.functional.log_softmax(scores,dim=1)
print(log_prob)
'''
tensor([[-2.7073, -1.4073, -0.4073, -5.2073, -5.4573, -5.4573, -4.7073]])
'''
# In[3]
# compute loss
n = 3.
mask = torch.tensor([[1,1,1,0,0,0,0]]) # number of 1 is n
loss = -1*n*torch.log(torch.tensor([[n]])) - torch.sum(log_prob*mask,dim=1,keepdim=True)
print(loss)
loss = loss.mean()
print(loss)
'''
tensor([[1.2261]])
tensor(1.2261)
'''

该示例代码仅展现了batch_size为1的情况, 在batch_size大于1时, 每一条数据都有不同的m和n, 为了能一起送入模型计算分值, 需要灵活的使用mask. 本人在实际使用该损失函数时,一共使用了两种mask, 分别mask每条数据所有候选文档和每条数据的相关文档, 供大家参考使用.

3.3 效果评估和使用经验

由于评测数据使用的是内部数据, 代码和数据都无法公开, 因此只能对使用效果做简单总结:

1. 效果优于Pointwise和Pairwise, 但差距不是特别大
2. 相比Pairwise收敛速度极快, 训练一轮基本就可以达到最佳效果

下面是个人使用经验:

1. 该损失函数比较占用显存, 实际的batch_size是batch_size*(m+n), 建议显存在12G以上
2. 负例数量越多,效果越好, 收敛也越快
3. 用pytorch实现log_softmax时, 不要自己实现, 直接使用torch中的log_softmax函数, 它的效率更高些.
4. 只有一个正例, 还可以考虑转为分类问题,使用交叉熵做优化, 效果同样较好

4 总结

该损失函数还是比较简单的, 只需要简单的数学知识就可以自行推导, 在实际使用中也取得了较好的效果, 希望也能够帮助到大家. 如果大家有更好的做法欢迎告诉我.

文章可以转载, 但请注明出处:

• 本人简书社区主页

• 本人博客园社区主页

• 本人知乎主页

• 本人Medium社区主页