【字符串算法】AC自动机

国庆后面两天划水，甚至想接着发出咕咕咕的叫声。咳咳咳，这些都不重要!最近学习了一下AC自动机，发现其实远没有想象中的那么难。

AC自动机的来历

我知道，很多人在第一次看到这个东西的时侯是非常兴奋的。（别问我为什么知道）

但AC自动机并不是能自动AC的程序。。。

AC自动机之所以叫AC自动机，是因为这个算法原名叫 Aho-Corasick automaton，是一个叫Aho-Corasick 的人发明的。

所以AC自动机也叫做 Aho-Corasick 算法

该算法在1975年产生于贝尔实验室，是著名的多模匹配算法。

AC自动机的用处

那么有的同学可能就有疑问了，AC自动机又不能自动AC，有什么作用呢？

其实AC自动机和KMP的用法相似，都是用来解决字符串的匹配问题的；但不一样的是，AC自动机更多的被用来解决多串的匹配问题，换言之，就是有多个子串需要匹配的KMP问题。

例如，例如给几个单词 acbs，asf,dsef；

再给出一个 很长的文章（句子），acbsdfgeasf；

问在这个文章中，总共出现了多少个单词，或者是单词出现的总次数，这就是AC自动机要解决的问题了。

AC自动机的实现方法

AC 自动机是 以 Trie 的结构为基础 ，结合 KMP 的思想 建立的。

简单来说，建立一个 AC 自动机有两个步骤：

1. 基础的 Trie 结构：将所有的模式串构成一棵 Trie。
2. KMP 的思想：对 Trie 树上所有的结点构造失配指针。

然后就可以利用它进行多模式匹配了。

不明白trie的同学可以 点击这里学习

不了解KMP的同学可以点击这里学习

所以就让我们一起来一步一步实现AC自动机吧！

定义一颗字典树

首先我们需要定义一颗字典树，我们用struct来实现各个节点的定义:

struct node
{
    int next[27];
    int fail;
    int count;
    void init()
    {
        memset(next,-1,sizeof(next));
        fail=0;
        count=0;
    }
}s[1100001];

存储后驱值的next[]数组

next[]数组就是正常Trie树里用来存储每个字符的后一个字符在s数组里的位置，比如我们读入一个字符串APPLE，那么：

s【1】存储的是A，它的next【P】=2，其余为-1；

s【2】存储的是P，它的next【P】=3，其余为-1；

s【3】存储的是P，它的next【L】=4，其余为-1；

s【4】存储的是L，它的next【E】=5，其余为-1；

s【5】存储的是E，它的next都为-1。

fail：失败指针

fail为失败指针，这个在后面的构造会讲到如何快速构造，那么有什么用呢？

我们来举个例子，这个例子这只显示了e的失配指针：

我们假设读入了she，shr，say，her四个单词，于是我们就得到了一棵可爱的字典树：

然后我们就只先构造一个失败指针：

例如匹配文章：sher，我们刚开始从s开始一直向左边走，走到e后发现：呀，没有路继续走了，如果暴力的从h开始又开始一轮匹配就极为浪费时间；这时我们就像，能不能利用之前的匹配信息呢？可以的！her的前缀he刚好和she的he相同，所以我们在she匹配失败的时候，就跳到了he后面继续匹配，发现r与r匹配！这就是fail指针的用处，是不是发现和KMP的next数组非常类似啊！

记录结尾的count

如果我插入一个单词APPLE，插入到最后E了，发现这个单词再也没有后面的字母了，这时我们就在这个E的count里面加上一个1，表示有1个单词以这个e作为结尾。

初始化的init()

我们在这里还定义了一个初始化函数init()，就是在开创到一个新起点时用来初始化一下的。

在字典树中插入单词

我们还是结合程序来讲解：

int ins()
{
    int len=strlen(str+1);
    int ind=0,i,j;

    for(int i=1;i<=len;i++)
    {
        j=str[i]-'a'+1;
        if(s[ind].next[j]==-1)
        {
            num++;
            s[num].init();
            s[ind].next[j]=num;
        }
        ind=s[ind].next[j];

    }
    s[ind].count++;
    return 0;
}

首先str数组就是我们要读入的字符串，ind表示我现在在s【】数组中的位置；接下来我们开始循环——对于每一个点：

如果他的前一个字母的next没有指向他的字母，那么我们就开创一个新点来存储这个字母，并且让他前一个字母的next指向它；

如果有直接指向它的字母的位置，那就直接跳过去就好了！

最后别忘了在每个单词的末尾的count加上1。

重点！！！快速构造fail指针

fail指针有什么用

首先，fail指针有什么用？我们继续使用上一个例子：

我们发现，左边的e的fail指针指向l最右侧的e，那么这个指针的含义是什么呢？我们不妨当一个点i指向了一个点j时，我们设从j开始，向上走L个字符就到了最顶点，其中从顶点到j的字符串为s；

在这个例子中，s为“he”，长度为L，也就是2；接着从i开始，向上再走L-1个字符，得到一个字符串ss，在这个例子中，ss也为“he”！

这时我们就惊讶的发现，s与ss相同！！

我们得知，当i的fail指针指向j，顶点到j的字符串s是顶点到i的字符串的后缀！

这样如果i继续往下匹配失败的话，就可以不用从头开始匹配，而是直接从他的fail开始匹配！节省了大量时间！这就是fail指针的精髓所在！

fail指针如何构造

我们先贴上代码：

int make_fail()
{
    int head=1,tail=1;
    int ind,ind_f;
    for(int i=1;i<=26;i++)
    {
        if(s[0].next[i]!=-1)
        {
            q[tail]=s[0].next[i];
            tail++;
        }
    }
    while(head<tail)
    {
        ind=q[head];
        for(int i=1;i<=26;i++)
        {
            if(s[ind].next[i]!=-1)
            {
                q[tail]=s[ind].next[i];
                tail++;

                ind_f=s[ind].fail;

                while(ind_f>0 && s[ind_f].next[i]==-1)
                ind_f=s[ind_f].fail;

                if(s[ind_f].next[i]!=-1)ind_f=s[ind_f].next[i];
                s[s[ind].next[i]].fail=ind_f;
            }
        }
        head++;
    }
    return 0;
}

首先我们需要开启一个队列q，存储需要处理的点；

接着我们把所有与顶点相连的点加入到队列里，然后我们对于队列里的每个数进行操作：

首先将他的所有儿子都加到队列尾部，然后作为一个负责任的父亲节点，肯定不能只把儿子们丢到队尾就完事了，还有做好工作——帮儿子们做好fail指针——

首先假如我是那个父亲节点x，对于字母a子节点，我先看一下我的fail指针指向的节点y，看一下y有没有字母a子节点z，如果有，就太好了，我就让我的子节点的fail指针指向z；

如果没有，那就从y出发，继续看他fail指向的点的有没有字母a的子节点……直到找到满足条件的点。

如果实在没办法，就算fail一路跳到0号节点也找不到，那就没办法了，我的字母a子节点的fail就只好指向0号节点了【因为初始化就为0，所以此时就不用操作了】

我们举个具体的栗子来看看：

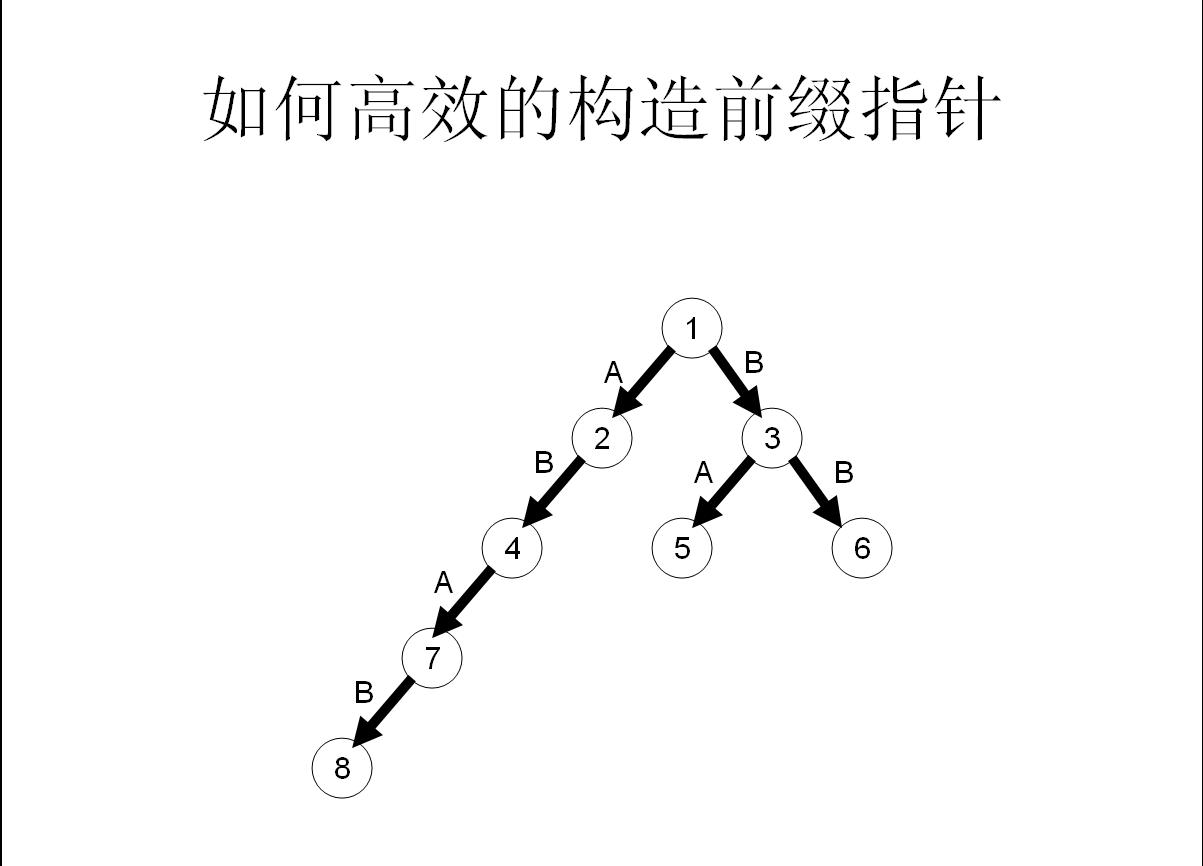
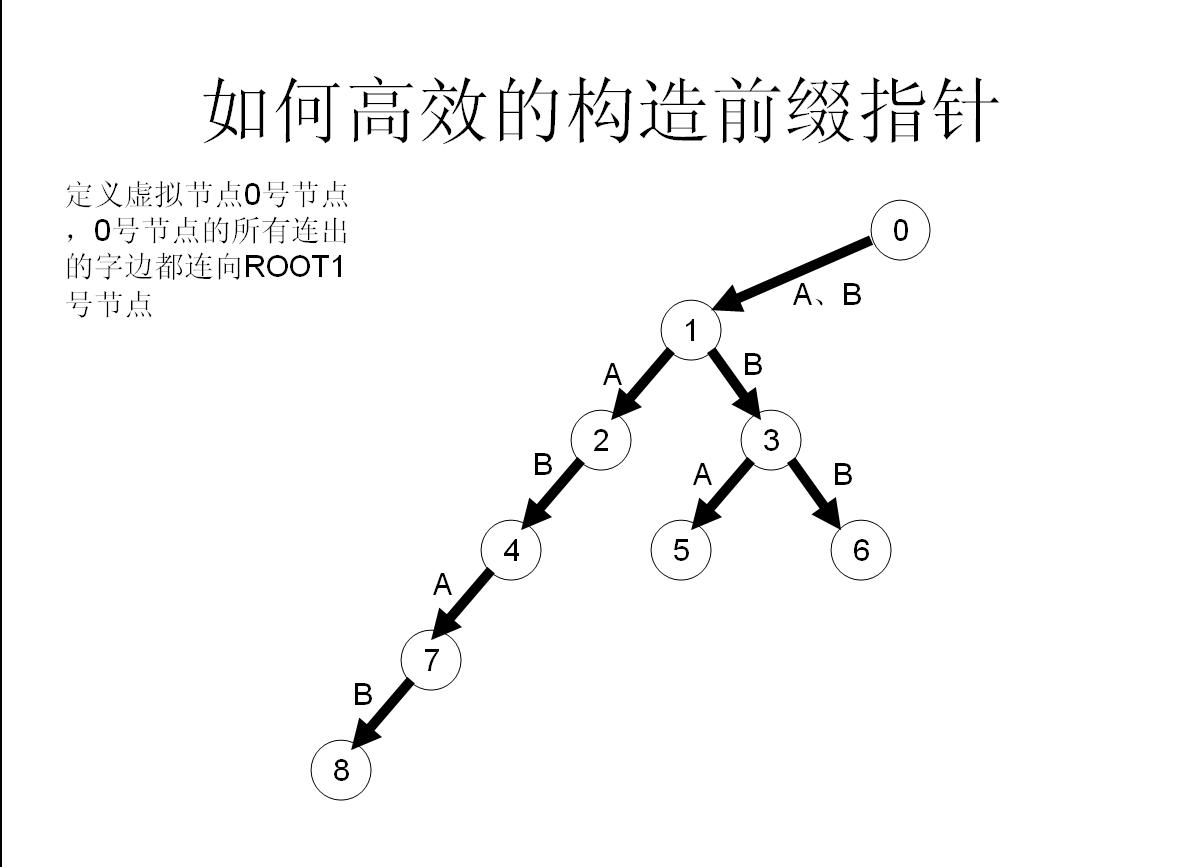
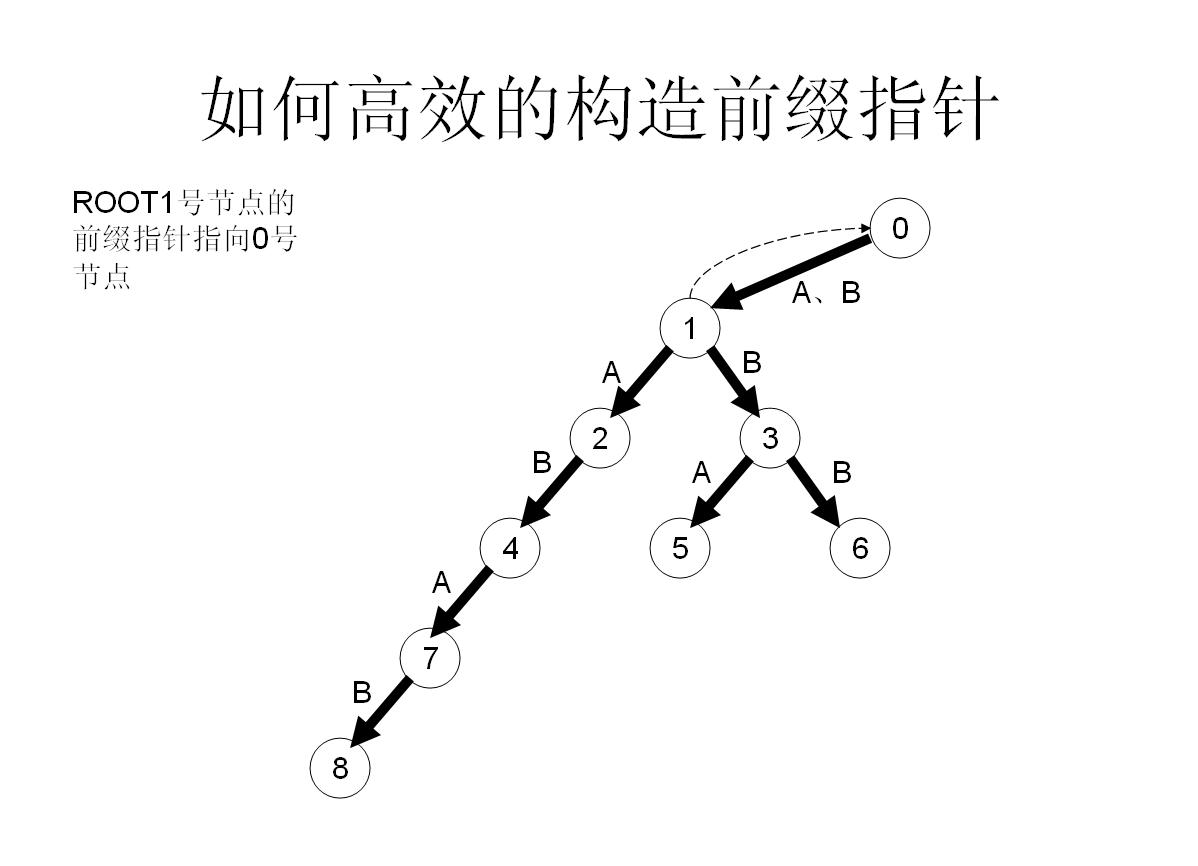
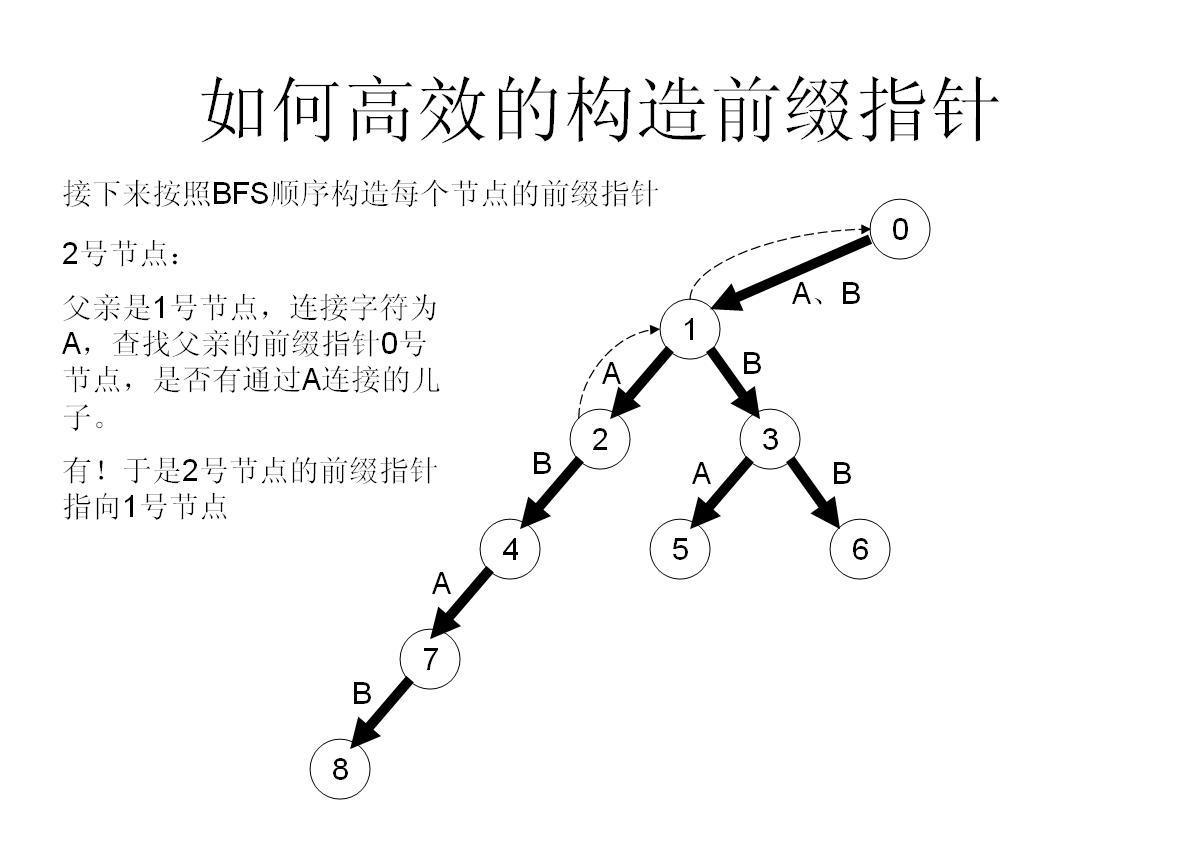
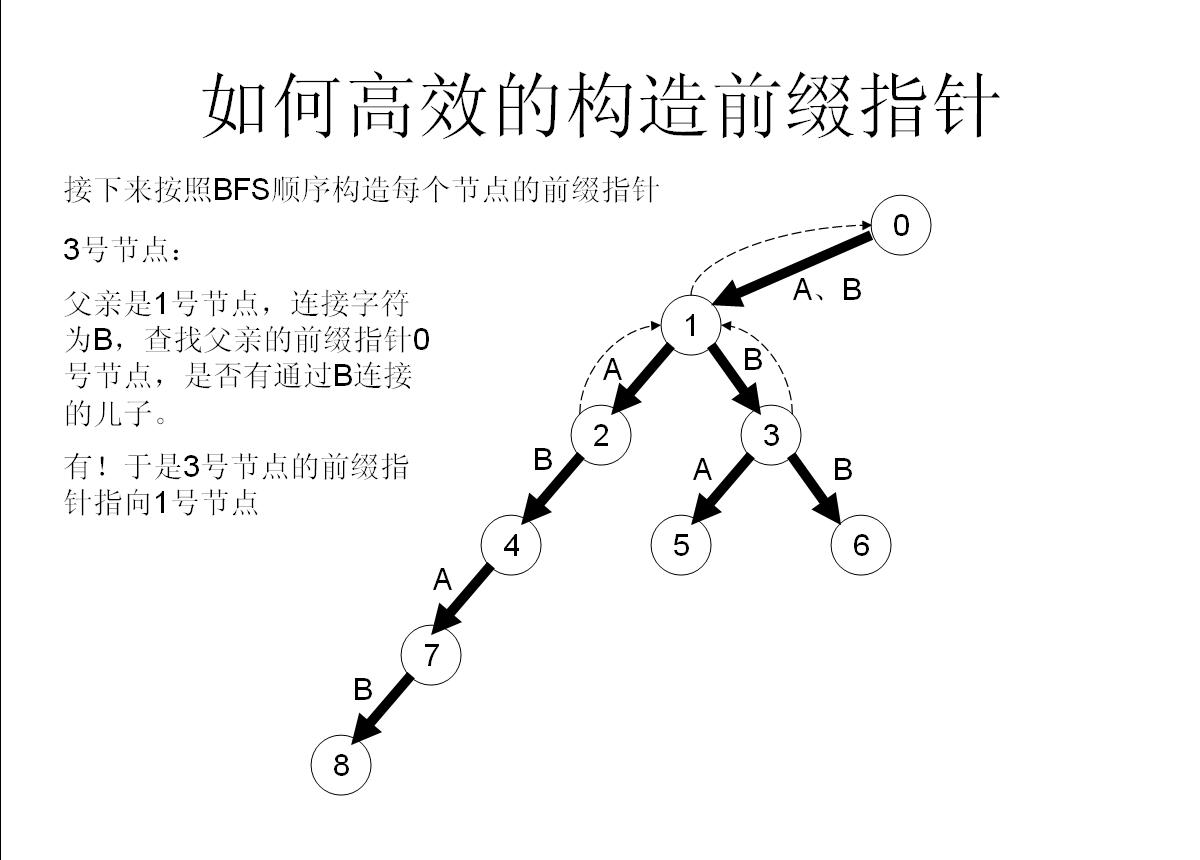
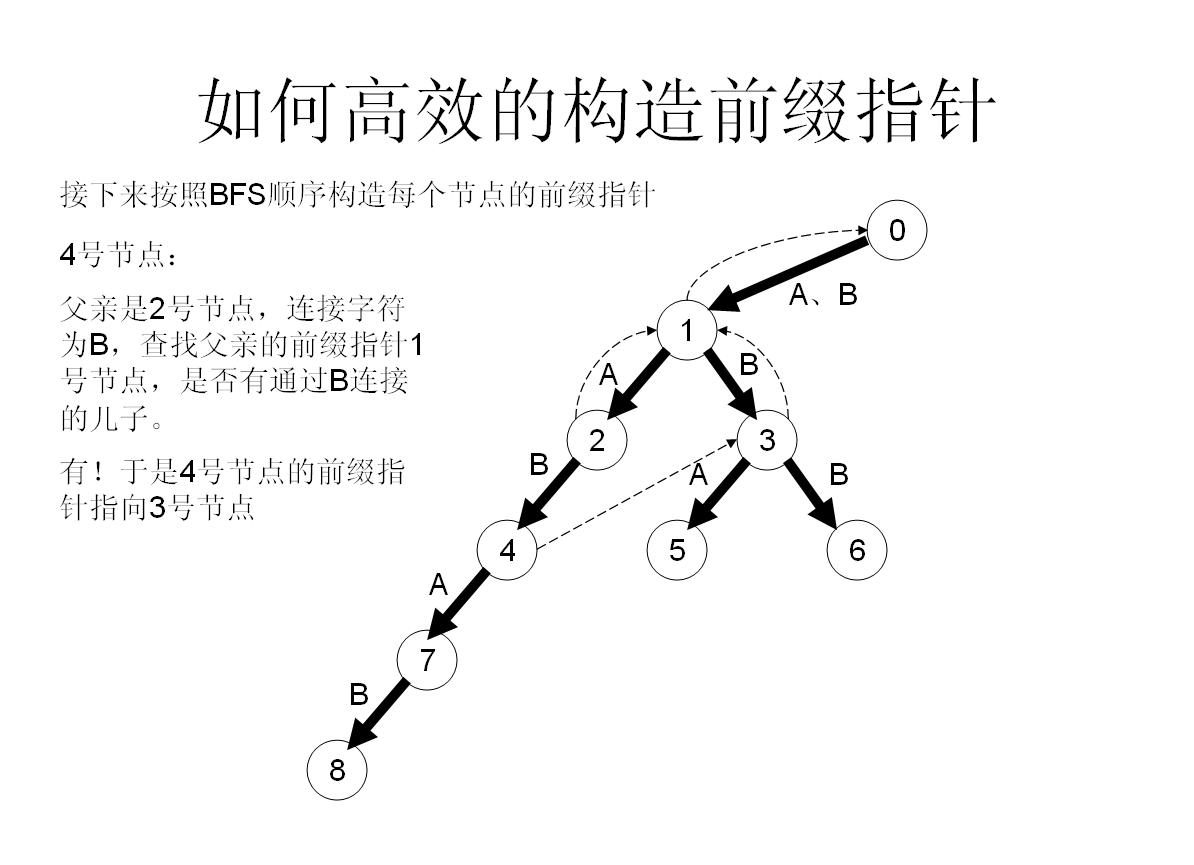
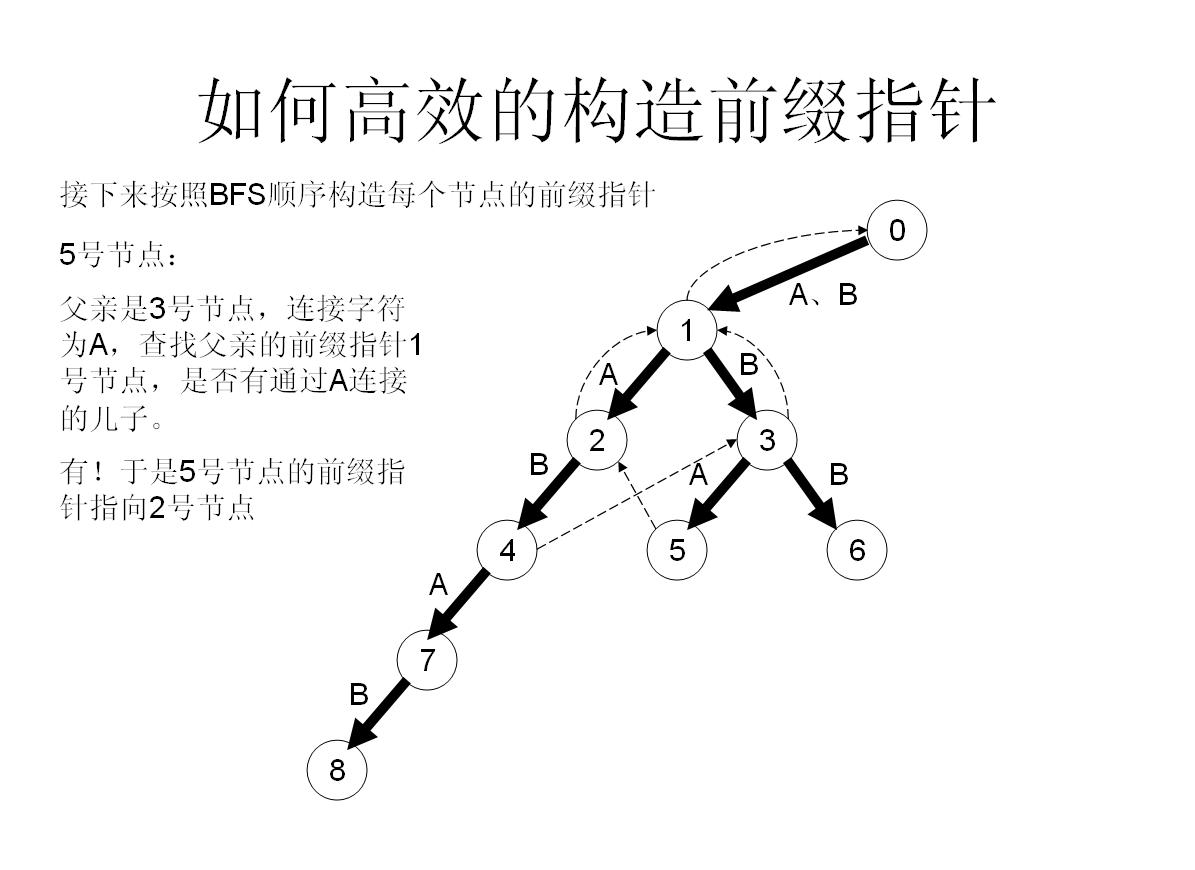
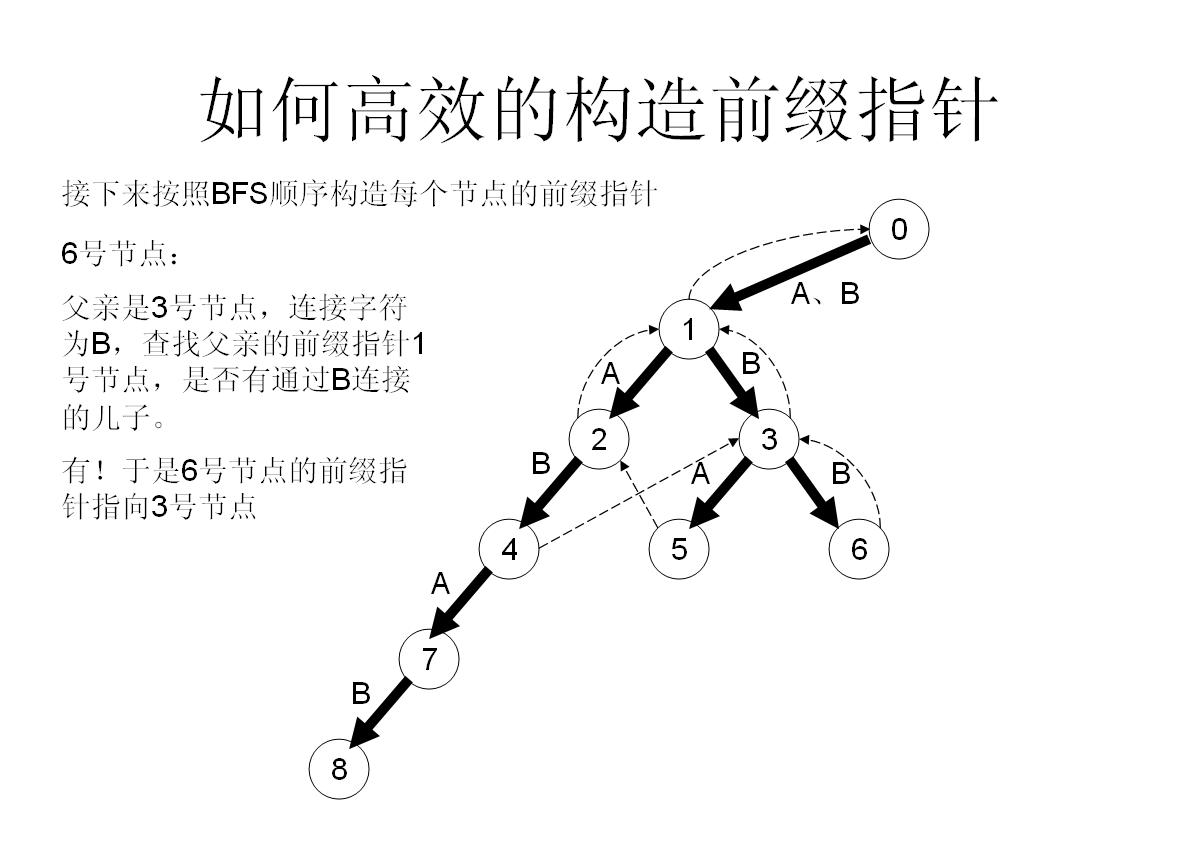
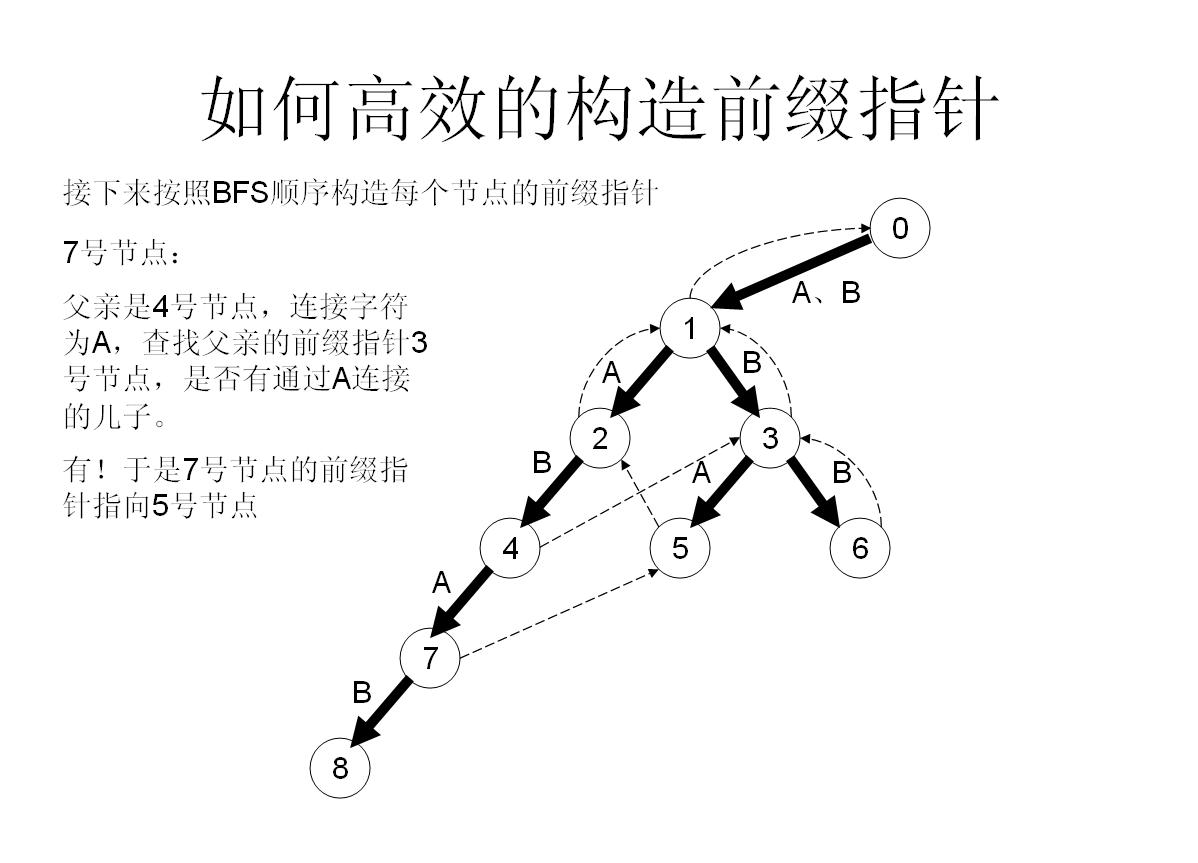
所以这样操作就可以快速构造fail指针了！

进行树上KMP

我们先看一下代码：

int find()
{
    int len=strlen(des+1);
    int j,ind=0;
    for(int i=1;i<=len;i++)
    {
        j=des[i]-'a'+1;
        while(ind>0 && s[ind].next[j]==-1)ind=s[ind].fail;

        if(s[ind].next[j]!=-1)
        {
            ind=s[ind].next[j];
            p=ind;
            while(p>0 && s[p].count!=-1)
            {
                ans=ans+s[p].count;
                s[p].count=-1;
                p=s[p].fail;
            }
        }
    }
    return 0;
}

一样的，ind表示我当前匹配好了的点，如果当前点不继续和IND的任何一个子节点相同，那么我就跳到ind的fail指针指向的点……知道找到与当前点匹配，或者跳到了根节点，与KMP十分相同！

需要注意的是由于这道题是求解哪些点在母串中出现，所以我们进行了一层优化：

while(p>0 && s[p].count!=-1)
 {
     ans=ans+s[p].count;
     s[p].count=-1;
     p=s[p].fail;
 }

就是当我们匹配好到一个串s【从根节点到IND的串】的时候，我们就往它的fail一直跳，由于他的fail到根节点的字符串ss一定是s的后缀，所以ss在母串中也一定出现，这时就加上它的count再设置为-1，防止后续重复访问就好了!

模板题

[Luogu p3808]

题目背景

这是一道简单的AC自动机模板题。

用于检测正确性以及算法常数。

为了防止卡OJ，在保证正确的基础上只有两组数据，请不要恶意提交。

管理员提示：本题数据内有重复的单词，且重复单词应该计算多次，请各位注意

题目描述

给定n个模式串和1个文本串，求有多少个模式串在文本串里出现过。

输入输出格式

输入格式：

第一行一个n，表示模式串个数；

下面n行每行一个模式串；

下面一行一个文本串。

输出格式：

一个数表示答案

输入输出样例

输入样例#1： 复制

2

a

aa

aa

输出样例#1： 复制

2

说明

subtask1[50pts]:∑length(模式串)<=10^6,length(文本串)<=10^6,n=1；

subtask2[50pts]:∑length(模式串)<=10^6,length(文本串)<=10^6；

就是模板题，下面给出模板：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
    int next[27];
    int fail;
    int count;
    void init()
    {
        memset(next,-1,sizeof(next));
        fail=0;
        count=0;
    }
}s[1100001];

int i,j,k,m,n,o,p,js,jl,jk,len,ans,num;
char str[1100000],des[1100000];
int q[1100000];

int ins()
{
    int len=strlen(str+1);
    int ind=0,i,j;

    for(int i=1;i<=len;i++)
    {
        j=str[i]-'a'+1;
        if(s[ind].next[j]==-1)
        {
            num++;
            s[num].init();
            s[ind].next[j]=num;
        }
        ind=s[ind].next[j];

    }
    s[ind].count++;
    return 0;
}

int make_fail()
{
    int head=1,tail=1;
    int inf,inf_f;
    for(int i=1;i<=26;i++)
    {
        if(s[0].next[i]!=-1)
        {
            q[tail]=s[0].next[i];
            tail++;
        }
    }
    while(head<tail)
    {
        inf=q[head];
        for(int i=1;i<=26;i++)
        {
            if(s[inf].next[i]!=-1)
            {
                q[tail]=s[inf].next[i];
                tail++;

                inf_f=s[inf].fail;

                while(inf_f>0 && s[inf_f].next[i]==-1)
                inf_f=s[inf_f].fail;

                if(s[inf_f].next[i]!=-1)inf_f=s[inf_f].next[i];
                s[s[inf].next[i]].fail=inf_f;
            }
        }
        head++;
    }
    return 0;
}

int find()
{
    int len=strlen(des+1);
    int j,ind=0;
    for(int i=1;i<=len;i++)
    {
        j=des[i]-'a'+1;
        while(ind>0 && s[ind].next[j]==-1)ind=s[ind].fail;

        if(s[ind].next[j]!=-1)
        {
            ind=s[ind].next[j];
            p=ind;
            while(p>0 && s[p].count!=-1)
            {
                ans=ans+s[p].count;
                s[p].count=-1;
                p=s[p].fail;
            }
        }
    }
    return 0;
}

int main()
{
    scanf("%d",&m);

    num=0;s[0].init();
    for(int i=1;i<=m;i++)
    {
        scanf("%s",str+1);
        ins();
    }

    scanf("%s",des+1);

    ans=0;

    make_fail();

    find();

    printf("%d",ans);
    return 0;
}

结语

通过这篇博客相信你一定已经学会了AC自动机！希望你喜欢这篇blog！！！