机器学习笔记簿降维篇 PCA 01

降维是机器学习中十分重要的部分，降维就是通过一个特定的映射（可以是线性的或非线性的）将高维数据转换为低维数据，从而达到一些特定的效果，所以降维算法最重要的就是找到这一个映射。主成分分析（Principal Component Analysis, PCA）是一种最经典，也是最简单的降维算法。PCA可以保证降维之后，重构回原数据的效果最好，因此广泛用于对高维数据的预处理。

1. 一个投影的PCA求解

设样本矩阵为\(X=[x_1,x_2,\cdots,x_n]\in \mathbb R^{m\times n}\)，其中样本向量\(x_i\in\mathbb R^m\)，样本均值为

\[\bar x=\frac1n\sum_{i=1}^nx_i
\]

我们现在要找到一个投影向量\(p\in\mathbb R^m\)，且\(\|p\|_2=1\)，将各样本映射到一个\(1\)维空间中，

\[y=p^Tx\in\mathbb R
\]

在这里，\(p^Tx\)称为一个主成分。

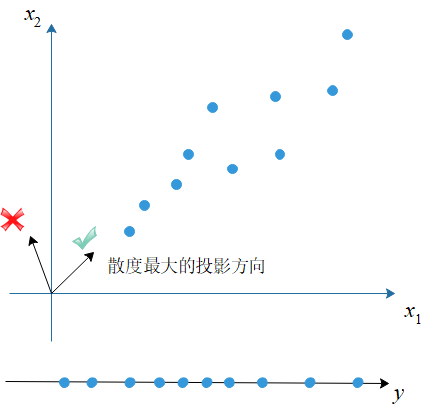
PCA的目标是最大化投影后的样本方差，方差也可以称为样本的散度，方差越大则样本的散度越大（样本点在空间中的分布越散乱），相反，如果散度越小，样本投影之后越聚集，就越难以重构（可以结合信息熵来理解，熵值越大信息越多）。最大化散度的方案可以保证投影产生的信息丢失最少，因此PCA总可以保证降维之后的数据是最接近原数据的。在当前情形下，PCA的优化问题是：

\[\begin{eqnarray*}
&&\max_{p^Tp=1} \sum_{i=1}^n{(y-\bar y)^2}\\
=&&\max_{p^Tp=1} \sum_{i=1}^n{(p^Tx-p^T\bar x)^2}\\
=&&\max_{p^Tp=1} \sum_{i=1}^n{(p^Tx-p^T\bar x)(p^Tx-p^T\bar x)^T}\\
=&&\max_{p^Tp=1} \sum_{i=1}^n{p^T(x-\bar x)(x-\bar x)^Tp}\\
=&&\max_{p^Tp=1} p^T\left[\sum_{i=1}^n{(x-\bar x)(x-\bar x)^T}\right]p\\
=&&\max_{p^Tp=1} p^TSp\tag{1}
\end{eqnarray*}
\]

其中，定义散度矩阵（亦称作协方差矩阵）为

\[S=\sum_{i=1}^n{}(x-\bar x)(x-\bar x)^T=\hat X\hat X^T
\]

这里\(\hat X\)是去中心化后的样本矩阵，即\(\hat X=[x_1-\bar x,x_2-\bar x,\cdots,x_n-\bar x]\)，考虑到\((1)\)中含有等式约束，我们可以用使用拉格朗日乘数法解优化问题\((1)\)，首先定义拉格朗日函数为

\[L(p,\lambda)=p^TSp+\lambda(1-p^Tp)
\]

令\(L\)对\(p\)的偏导为\(0\)得到：

\[\begin{eqnarray*}
\frac{\partial L}{\partial p}&=&Sp-\lambda p=0\\
\Rightarrow Sp&=&\lambda p\tag{2}
\end{eqnarray*}
\]

将\((2)\)代回\((1)\)中得到

\[\begin{eqnarray*}
&&\max_{p^Tp=1}{p^TSp}\\=&&\max_{p^Tp=1}{p^T\lambda p}\\=&&\max_{p^Tp=1}{\lambda}\tag{3}
\end{eqnarray*}
\]

显然\((2)\)是一个特征值问题，根据\((3)\)可以知道，最大的特征值对应的特征向量就是我们所需的投影向量\(p\)。

2. 多个投影的PCA求解

在前面我们获得了一个投影向量，可以将样本投影到一维空间，在一般情况下我们需要指定降维维数\(d\)，这样就需要\(d\)个投影向量。这样我们的目标就是一个投影矩阵\(P=[p_1,p_2,\cdots,p_d]\in\mathbb{R}^{m\times d}\)，并且\(P\)的各个投影\(p_i\)都是标准正交的（正交性可以保证每一个主成分之间都互不相关），也即\(P^TP=I\)。样本可以通过\(P\)投影到\(d\)维空间：

\[y=P^Tx\in\mathbb R^d
\]

\(y\)中的每一个元素都是一个主成分，此处它包含了个\(d\)个互不相关的主成分。

PCA的优化目标仍然是最大化样本的散度，同理，它的优化目标是：

\[\begin{eqnarray*}
&&\max_{P^TP=I} \sum_{i=1}^n{\|y-\bar y\|^2_2}\\
=&&\max_{P^TP=I} \sum_{i=1}^n{\|P^Tx-P^T\bar x\|^2_2}\\
=&&\max_{P^TP=I} \sum_{i=1}^n{tr\left[(P^Tx-P^T\bar x)(P^Tx-P^T\bar x)^T\right]}\\
=&&\max_{P^TP=I} \sum_{i=1}^n{tr\left[P^T(x-\bar x)(x-\bar x)^TP\right]}\\
=&&\max_{P^TP=I} tr\left\{P^T\left[\sum_{i=1}^n{(x-\bar x)(x-\bar x)^T}\right]P\right\}\\
=&&\max_{P^TP=I} tr(P^TSP)\\
=&&\max_{p_i^Tp_i=1} \sum_{i=1}^n{p_i^TSp_i}\tag{4}
\end{eqnarray*}
\]

这里\((4)\)和\((1)\)具有相同的形式，我们仍然可以通过拉格朗日乘数法来求解，而这里我们获得的投影矩阵是\(S\)的前\(d\)个最大特征值对应的特征向量依次排列组成的。

一般我们定义能量占比来选取\(d\)的大小，设定一个阈值\(\alpha\)（一般取\(0.95,0.98\)等），则\(d\)由下式给出

\[\min_{d}\left\{d\ |\ E=\frac{\sum_{i=1}^d \lambda_i}{\sum_{i=1}^n\lambda_i}>\alpha\right\}
\]

\(\lambda_i\)是第\(i\)大的特征值，\(E\)是能量占比，这个式子的意义是，选择能够使能量占比达到阈值的最小的\(d\)作为降维维数，这样可以保证主要的信息（也就是特征值大的那些投影）能够被获取，那些特征值很小的投影被丢弃，PCA通过这种方式可以去除散度矩阵的零空间，从而去除了原样本的无用信息。

总结一下，PCA的步骤很简单：

计算去中心化后的样本矩阵矩阵\(\hat X\)，求出散度矩阵\(S\)
对散度矩阵\(S\)进行特征分解
最后取它前\(d\)个最大特征值的特征向量作为投影矩阵\(P\)。

3. 基于最小化重构误差的理解

以上我们从最大化散度的角度出发理解了PCA。由于PCA本质上要求降维产生的数据信息的损失最少，因此我们可以从最小化重构误差的角度出发，也能得到相同的结果。

首先我们需要知道投影后的数据是如何重构的，在这里重构就是投影的逆过程，重构数据就因此被定义为

\[x'=Py=PP^Tx
\]

在这里，PCA想要做到重构后的数据可以近似为原始数据，即

\[x'=y_1p_1+y_2p_2+\cdots+y_dp_d\approx x
\]

这里的\(y_ip_i(i=1,2,\cdots,d)\)其实是数据的每一个投影分量。也就是说我们希望误差\(\|x-x'\|_2\)越小越好，对应的优化问题是

\[\begin{eqnarray*}
&&\min_{P^TP=I}\sum_{i=1}^n{\|x_i-x_i'\|_2^2}\\
=&&\min_{P^TP=I}\sum_{i=1}^n{\|x_i-PP^Tx_i\|_2^2}\\
=&&\min_{P^TP=I}{\|X-PP^TX\|_F^2}\\
=&&\min_{P^TP=I}tr\left[(X-PP^TX)(X-PP^TX)^T\right]\\
=&&\min_{P^TP=I}tr(XX^T)-2tr(XX^TPP^T)+tr(PP^TXX^TPP^T)\\
=&&\min_{P^TP=I}tr(P^TXX^TPP^TP)-2tr(P^TXX^TP)\\
=&&\min_{P^TP=I}-tr(P^TXX^TP)\\
=&&\max_{P^TP=I}tr(P^TXX^TP)\\
\end{eqnarray*}
\]

如果假设散度矩阵是\(S_0=XX^T\)，则原优化问题变为

\[\max_{P^TP=I}tr(P^TS_0P)
\]

这个问题我们已经很熟悉了：\(P\)就是\(S_0\)的前\(d\)个最大特征值对应的特征向量组成的。

注意到，在之前我们用到的散度矩阵是\(S=\hat X\hat X^T\)，这里的\(\hat X\)是去中心化过的样本矩阵，但根据以上的推导，样本矩阵完全可以不用去中心化，直接计算\(S_0\)进行特征分解依然可以实现PCA，但这不意味着用\(S\)和用\(S_0\)得到的计算结果是相同的：去中心化可以帮助减少样本数据偏移（bias）的影响，不去中心化时可以用更少的投影就达到很好的重构效果，在样本均值为\(0\)的时候，这两种方法没有区别。在实际应用中，使用\(S_0\)或者\(S\)作特征分解都是可行的。