4.12 省选模拟赛 LCA on tree 树链剖分 树状数组 分析答案变化量

LINK：duoxiao OJ LCA on Tree

题目：

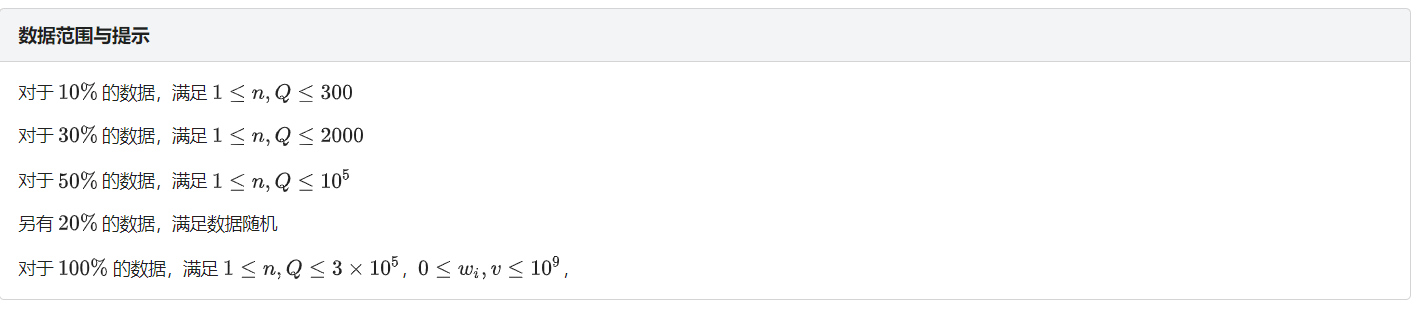
一道树链剖分+树状数组的神题。

(直接nQ的暴力有50.

其实对于树随机的时候不难想到一个算法 对于x的修改 暴力修改到根.

对于儿子的答案维护 不难发现维护几个变量值即可 这样做每次是Qh的复杂度 在树随机时为logn

考虑正解：

难点还是在于修改 先把起始的答案求出来。

对于修改x x的某个孙子w答案的变化显然是 (sz[w]+1)v.

对于x的某个儿子 s来说 答案的变化为 (sz[s]+1)v+\(v\cdot \sum_{tn\in son[s]}(sz[s]-sz[tn])\)

对于x来说 答案的变化为 (sz[x]+1)v+\(v\cdot \sum_{tn\in son[x]}(sz[x]-sz[tn])(|son[tn]|+1)\)

于是对于某个点的修改来说 访问父亲 父亲的父亲被修改的权值即可。

考虑对于x的祖宗的影响。

不难发现 对于某个祖宗y来说 如果d含有x这棵子树 得到的贡献为 \((sz[y]-sz[d])\cdot C(x,2)\cdot v\)

其中C(x,2)表示和x的距离不超过2的点数。

关键是对祖宗的维护 。

一个暴力：暴力向根修改O(h).

一个暴力：求出儿子内被修改的值总和 树状数组维护dfs序 logn son[x].

不过两个暴力都不靠谱。

神技 树链剖分。

可以发现 对于第一个暴力如果我们只考虑轻链的贡献 那么这种修改最多logn次 树剖后向上跳即可。

可以发现 对于一个点来说此时其发出的所有的轻链 都被暴力跳过了。

对于重链 由于只有一条 树状数组维护求出这个重链的儿子的修改总和即可。

复杂度nlogn.非常的妙。

const int MAXN=300010;
int n,Q,len,cnt;
ui f[MAXN],a[MAXN],c[MAXN],sum[MAXN],top[MAXN],w1[MAXN],s[MAXN],w2[MAXN];
int d[MAXN],sz[MAXN],son[MAXN],dfn[MAXN],f1[MAXN],f2[MAXN];
int lin[MAXN],ver[MAXN],nex[MAXN],fa[MAXN];
inline void add(int x,int y)
{
	ver[++len]=y;
	nex[len]=lin[x];
	lin[x]=len;
}
inline void dfs(int x,int father)
{
	fa[x]=father;sz[x]=1;d[x]=d[father]+1;
	sum[x]+=a[x];
	go(x)
	{
		dfs(tn,x);
		f[x]+=sz[x]*sum[tn]+sz[tn]*sum[x];
		sum[x]+=sum[tn];
		++f1[x];f2[x]+=f1[tn];
		sz[x]+=sz[tn];
		if(sz[son[x]]<sz[tn])son[x]=tn;
	}
	f[x]+=a[x]*2;
}
inline void dp(int x,int father)
{
	top[x]=father;dfn[x]=++cnt;
	if(!son[x])return;
	dp(son[x],father);
	go(x)if(tn!=fa[x]&&tn!=son[x])dp(tn,tn);
}
inline void dfs(int x)
{
	go(x)
	{
		if(tn==fa[x])continue;
		dfs(tn);
		w1[x]+=(f1[tn]+1)*(sz[x]-sz[tn]);
		w2[x]+=(sz[x]-sz[tn]);
	}
}
inline void add1(int x,int y)
{
	while(x<=n)
	{
		c[x]+=y;
		x+=x&(-x);
	}
	return;
}
inline ui ask(int x){ui cnt=0;while(x){cnt+=c[x];x-=x&(-x);}return cnt;}
inline void change(int x,int y)
{
	int s=x;y=y*(f1[x]+f2[x]+1);
	add1(dfn[x],y);
	while(fa[top[s]])
	{
		int fx=top[s];
		int fw=fa[fx];
		if(son[fw]!=fx)
			f[fw]+=(sz[fw]-sz[fx])*y;
		s=fw;
	}
}
inline ui query(int x)
{
	if(!son[x])return 0;
	return ask(dfn[son[x]]+sz[son[x]]-1)-ask(dfn[son[x]]-1);
}
int main()
{
	freopen("1.in","r",stdin);
	get(n);get(Q);
	rep(2,n,i){int get(x);add(x,i);}
	rep(1,n,i)get(a[i]);
	dfs(1,0);dp(1,1);dfs(1);
	rep(1,Q,i)
	{
		int op,x,y;
		get(op);get(x);
		if(op==1)
		{
			get(y);
			s[x]+=y;
			f[x]+=(sz[x]+1+w1[x])*y;
			change(x,y);
		}
		else
		{
			ui ans=f[x]+s[fa[x]]*(sz[x]+1+w2[x])+s[fa[fa[x]]]*(sz[x]+1);
			ans+=query(x)*(sz[x]-sz[son[x]]);printf("%u\n",ans);
		}
	}
	return 0;
}