Best Time to Buy and Sell Stock I II III IV

一、Best Time to Buy and Sell Stock I

Say you have an array for which the ith element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (ie, buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Example 1:

Input: [7, 1, 5, 3, 6, 4]
Output: 5

max. difference = 6-1 = 5 (not 7-1 = 6, as selling price needs to be larger than buying price)

Example 2:

Input: [7, 6, 4, 3, 1]
Output: 0

In this case, no transaction is done, i.e. max profit = 0.

 1 class Solution {
 2 public:
 3     //遍历一次，每次更新最小值，并且当前值与最小值相减，如果大于最大收入则更新最大收入
 4     int maxProfit(vector<int>& prices) {
 5         int len=prices.size();
 6         if(len==0) return 0;
 7         int Min=prices[0],res=0;
 8         for(int i=0;i<len;i++)
 9         {
10             if(prices[i]<Min) Min=prices[i];
11             res=res>(prices[i]-Min)?res:(prices[i]-Min);
12         }
13         return res;
14
15     }
16 };

二、Best Time to Buy and Sell Stock II

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times). However, you may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).

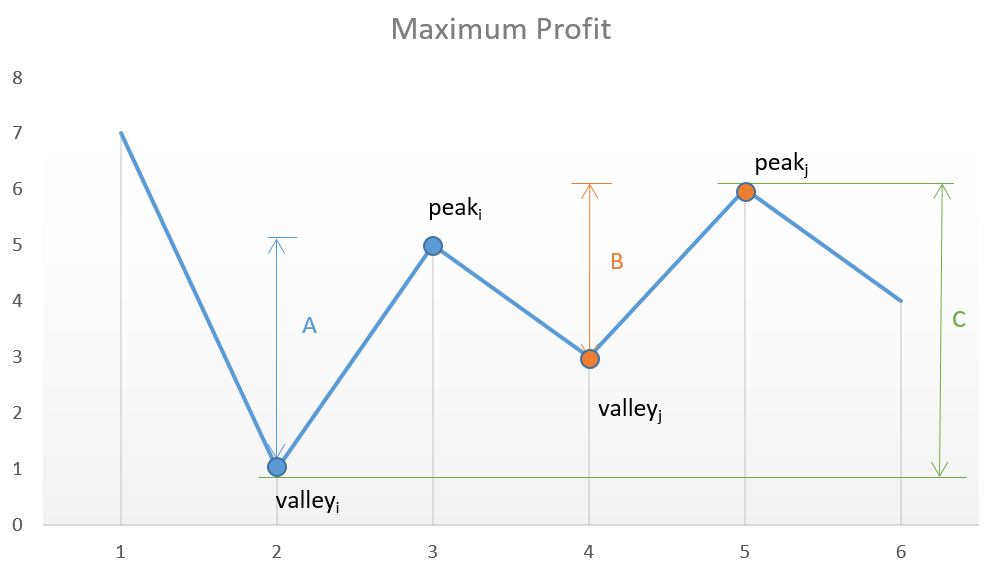
法一：所有的 低谷 与其 最近的 峰值的差  的和

 1 class Solution {
 2 public:
 3
 4     int maxProfit(vector<int>& prices) {
 5         int len=prices.size();
 6         if(len==0||len==1) return 0;
 7         int Max=0,i=1;
 8         while(i<len)
 9         {
10             while(i<len&&prices[i-1]>=prices[i])
11                 i++;
12             int valley=prices[i-1];
13             while(i<len&&prices[i-1]<prices[i])
14                 i++;
15             int peek=prices[i-1];
16             Max+=(peek-valley);
17         }
18         return Max;
19     }
20 };

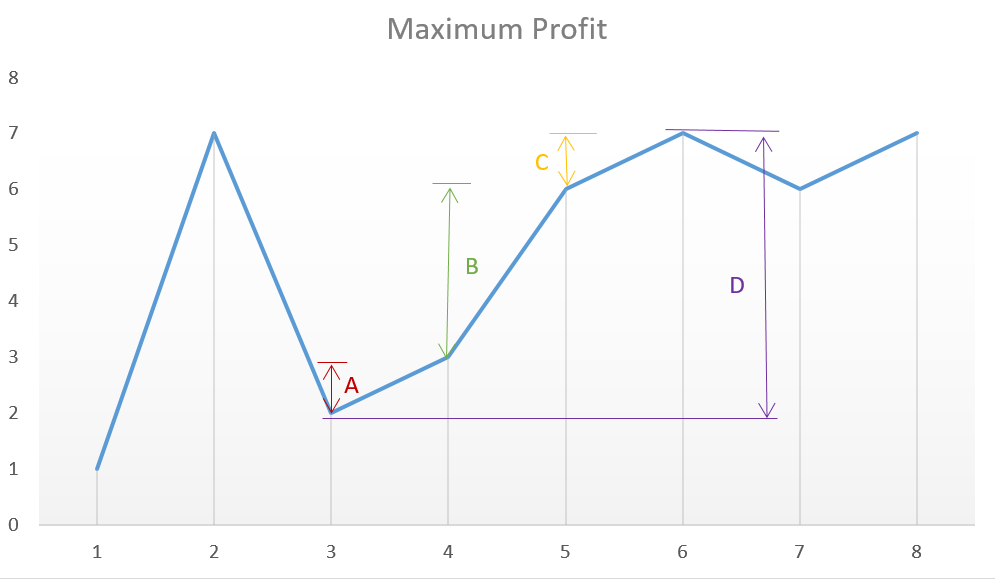
法二：

 1 class Solution {
 2 public:
 3    int maxProfit(vector<int>& prices)
 4    {
 5        int len=prices.size();
 6        if(len==0||len==1) return 0;
 7        int Max=0;
 8        for(int i=1;i<len;i++){
 9            if(prices[i-1]<prices[i])
10                Max+=(prices[i]-prices[i-1]);
11        }
12        return Max;
13    }
14 };

三、Best Time to Buy and Sell Stock III

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete at most two transactions.

Note:
You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).

 1 class Solution {
 2 public:
 3     //利用四个状态来解答这个题目,假设才开始手里有 0 块钱
 4     /*
 5     1、sell2[i]:前i天进行第二笔交易中的卖股票状态后剩余最多的钱
 6     2、buy2[i]:前i天进行第二笔交易中的买股票状态后剩余最多的钱
 7     3、sell1[i]:前i天进行第一笔交易中的卖股票状态后剩余最多的钱
 8     4、buy1[i]：
 9     sell2[i]=max(sell2[i-1],buy2[i-1]+prices[i]);
10     buy2[i]=max(buy2[i-1],sell1[i-1]-prices[i]);
11     sell1[i]=max(sell1[i-1],buy1[i-1]+prices[i]);
12     buy1[i]=max(buy1[i],-prices[i]);
13     */
14     int maxProfit(vector<int>& prices) {
15         int len=prices.size();
16         if(len==0||len==1) return 0;
17         int sell2=0;
18         int sell1=0;
19         int buy2=INT_MIN;
20         int buy1=INT_MIN;
21         for(int i=0;i<len;i++){
22             sell2=max(sell2,buy2+prices[i]);
23             buy2=max(buy2,sell1-prices[i]);
24             sell1=max(sell1,buy1+prices[i]);
25             buy1=max(buy1,-prices[i]);
26         }
27         return max(sell1,sell2);
28     }
29 };

四：Best Time to Buy and Sell Stock IV

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete at most k transactions.

 1 class Solution {
 2 public:
 3     //一次交易代表（买一次并且卖一次）当交易次数k大于数组长度的一半的时候，交易次数就会溢出，就相当于 随便交易求最大利润，就是用贪心解决(II)。
 4     /*如果交易次数不到一半
 5         采用动态规划来解决问题。
 6     我们需要维护如下两个量：
 7     global[i][j]:当前到达第i天最多可以进行j次交易，所得到的最大利润。
 8     local[i][j]:当前到达第i天最多可以进行j次交易，而且最后一次交易在当天卖出，所得到的最大利润。
 9     状态转移方程：
10     global[i][j] = max(local[i][j], global[i-1][j])
11     上述方程比较两个量的大小：①当前局部最大值；第i天交易了②过往全局最大值。到第i-1天进行j次交易的最大值，第i天没有交易
12     local[i][j] = max(global[i-1][j-1] + max(diff, 0), local[i-1][j] + diff)
13     上述方程比较两个量的大小：
14     ①全局到i-1天进行j-1次交易，然后加上今天的交易（如果今天的交易赚钱的话）。
15     ②取局部第i-1天进行j次交易，然后加上今天的差值（local[i-1][j]是第i-1天卖出的交易，它加上diff后变成第i天卖出，并不会增加交易次数。无论diff是正还是负都       要加上，否则就不满足local[i][j]必须在最后一天卖出的条件了）
16     */
17     int maxProfit(int k, vector<int>& prices) {
18         int len=prices.size();
19         if(len==0||len==1) return 0;
20         if(k>=len/2)  return quickSolve(prices);
21         int global[k+1]={0};
22         int local[k+1]={0};
23         int diff=0;
24         for(int i=1;i<len;i++)
25         {
26             diff=prices[i]-prices[i-1];
27             for(int j=k;j>=1;j--)
28             {
29                 local[j]=max(global[j-1]+max(diff,0),local[j]+diff);
30                 global[j]=max(global[j],local[j]);
31             }
32         }
33         return global[k];
34     }
35 private:
36     int quickSolve(vector<int>& prices)
37     {
38         int res=0;
39         for(int i=1;i<prices.size();i++)
40         {
41             if(prices[i]>prices[i-1]) res+=(prices[i]-prices[i-1]);
42         }
43         return  res;
44     }
45 };