NOIP 2016 洛谷 P2827 蚯蚓题解

题目传送门

展开

题目描述

本题中，我们将用符号[c]表示对c向下取整，例如：[3.0」= [3.1」=[3.9」=3。蛐蛐国最近蚯蚓成灾了！隔壁跳

蚤国的跳蚤也拿蚯蚓们没办法，蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。蛐蛐国里现在共有n只蚯蚓（n为正整

数)。每只蚯蚓拥有长度，我们设第i只蚯蚓的长度为a_i(i=1,2,...,n)，并保证所有的长度都是非负整数（即:可

能存在长度为0的蚯蚓）。每一秒，神刀手会在所有的蚯蚓中，准确地找到最长的那一只（如有多个则任选一个）

将其切成两半。神刀手切开蚯蚓的位置由常数p(是满足0<p<1的有理数)决定，设这只蚯蚓长度为x，神刀手会将其

切成两只长度分别为[px]和x-[px]的蚯蚓。特殊地，如果这两个数的其中一个等于0，则这个长度为0的蚯蚓也会被

保留。此外，除了刚刚产生的两只新蚯蚓，其余蚯蚓的长度都会增加q(是一个非负整常数)。蛐蛐国王知道这样不

是长久之计，因为蚯蚓不仅会越来越多，还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物，但是

救兵还需要m秒才能到来......(m为非负整数）蛐蛐国王希望知道这m秒内的战况。具体来说，他希望知道：?m秒内

，每一秒被切断的蚯蚓被切断前的长度（有m个数）?m秒后，所有蚯蚓的长度（有n+m个数)。蛐蛐国王当然知道怎

么做啦！但是他想考考你......

输入格式

第一行包含六个整数n,m,q,u,v,t，其中：n,m,q的意义见问题描述；

u,v,t均为正整数；你需要自己计算p=u/v(保证0<u<v)t是输出参数，其含义将会在输出格式中解释。

第二行包含n个非负整数，为ai,a2,...,an，即初始时n只蚯蚓的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。

保证1<=n<=10^5，0<m<7*10^6，0<u<v<10^9，0<=q<=200，1<t<71，0<ai<10^8。

输出格式

第一行输出[m/t]个整数，按时间顺序，依次输出第t秒，第2t秒，第3t秒……被切断蚯蚓（在被切断前）的长度。

第二行输出[(n+m)/t]个整数，输出m秒后蚯蚓的长度；需要按从大到小的顺序

依次输出排名第t，第2t，第3t……的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。即使某一行没有任何数需要输出，你也应输出一个空行。

请阅读样例来更好地理解这个格式。

输入输出样例

样例输入一

样例输出一

样例输入二

样例输出二

样例输入三

//空行

样例输出三

说明/提示

【数据范围】

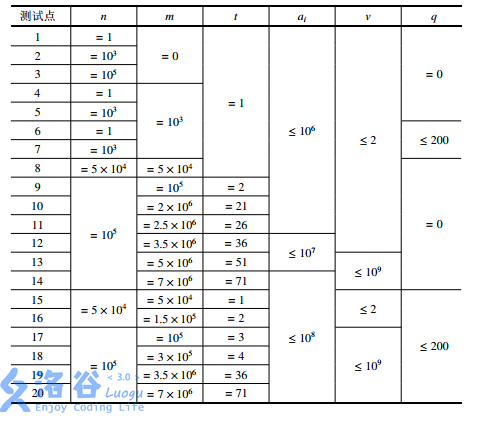
分析

m的最大值已经达到了7e6，这道题我们如果直接枚举的话肯定会超时

因为每次都要选出最长的蚯蚓将其切断，所以我们考虑一下它是否具有单调性

我们可以在把所有蚯蚓的长度读入后按照从大到小的顺序排一下序

这样的话，第一次我们肯定会将下标为1的蚯蚓取出将其切断

那么第二次呢？我们还会继续取下标为2的蚯蚓吗，这是不一定的

有可能最长的蚯蚓的长度很长，把它切断后它剩下的部分仍然要比之前长度第2长的蚯蚓要长

那我们可以怎么办呢

当我们切开一条蚯蚓时，必定会把它分成两部分

我们可以把其中较大的一个部分扔到一个大根堆中，再把其中较小的部分扔到另一个大根堆中

这样，我们每次在原数组和这两个大根堆中取一个最大值

把这个最大值作为切开的蚯蚓，按照上面的操作把切开的两部分分别扔到两个堆中

那么每次操作后蚯蚓的长度都会增加一个值q，这该怎么处理呢

把每个数都枚举一遍分别加上q显然是不现实的

我们可以开一个变量ad记录到当前的时间蚯蚓长度的增加量

比如过了1秒，ad=q,过了2秒，ad=2q……过了n秒,ad=nq

每次取出一个元素把它加上ad就可以了

但这时又有一个问题，被切断的蚯蚓在那一秒内长度是不会变化的，如果我们还给它加上ad，显然会出错

所以我们在把它放到堆中时，先将它的值减去ad

大家可以这样理解，这条蚯蚓是在第m秒生成的，

也就是说，在前m秒，它的长度并不会增加

这样如果没有任何处理的话，它的长度会多算在它被切割那一秒时的ad值，所以我们再把它放进堆中时，要把它的长度减去那一秒时的ad值

这样的话，我们就可以写出如下的代码

 #include<cstdio>

 #include<cstring>

 #include<algorithm>

 #include<iostream>

 #include<queue>

 using namespace std;

 typedef long long ll;

 const int maxn=+;

 ll a[maxn];

 bool cmp(ll aa,ll bb){ return aa>bb; }

 priority_queue<ll> qq,xi,da;

 int main(){

     ll n,m,q,u,v,t;

     scanf("%lld%lld%lld%lld%lld%lld",&n,&m,&q,&u,&v,&t);

     for(ll i=;i<=n;i++){

         scanf("%lld",&a[i]);

     }

     sort(a+,a++n,cmp);

     ll head=,tail=n;

     ll js=,ad=;

     while(m--){

         js++;

         ll ans=-0x3f3f3f3f3f3f3f3f;

         ll bb=ans,cc=ans,dd=ans;

         if(!xi.empty())  bb=xi.top();

         if(!da.empty()) cc=da.top();

         if(head<=tail) dd=a[head];

         ans=max(max(ans,bb),max(cc,dd));

         if(ans==bb) xi.pop();

         else if(ans==cc) da.pop();

         else head++;

         ans+=ad;

         if(js%t==) printf("%lld ",ans);

         ad=js*q;

         ll left=u*ans/v;

         ll right=ans-left;

         left-=ad,right-=ad;

         xi.push(min(left,right));

         da.push(max(left,right));

     }

     printf("\n");

     for(ll i=head;i<=tail;i++) {qq.push(a[i]);}

     while(!xi.empty()) {qq.push(xi.top()),xi.pop();}

     while(!da.empty()) {qq.push(da.top()),da.pop();}

     ll cnt=;

     while(!qq.empty()){

         cnt++;

         if(cnt%t==) printf("%lld ",qq.top()+ad);

         qq.pop();

     }

     printf("\n");

     return ;

 }

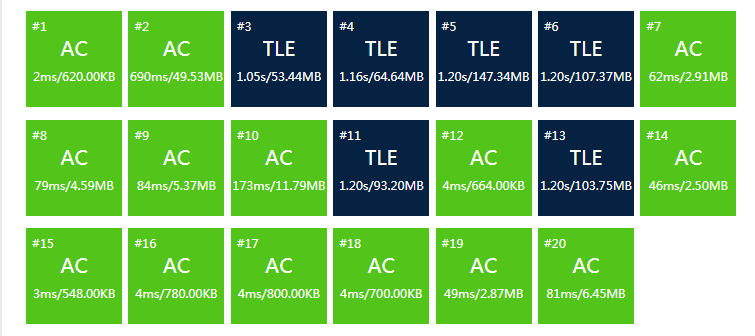
这样写T掉是必然的，因为你用优先队列的话，每次插入时间复杂度都为O（logn）

这样的效率肯定会有数据T掉

那么我们再仔细想想，发现其实是没有必要用优先队列的

因为我们每一次都是先把最长的蚯蚓切割，所以先切的蚯蚓一定长于后切的蚯蚓

所以先切的蚯蚓的较长的部分一定长于后切的蚯蚓较长的部分，所以先切的蚯蚓的较短的部分一定长于后切的蚯蚓较短的部分

所以用来储存切割后两部分的两个堆都具有单调性，因此我们可以用数组模拟，这样会快很多

 #include<cstdio>

 #include<cstring>

 #include<algorithm>

 #include<iostream>

 #include<queue>

 using namespace std;

 #define maxn 7000005

 #define ll long long

 ll a[maxn],xi[maxn],da[maxn];

 bool cmp(ll aa,ll bb){ return aa>bb; }

 int main(){

     ll n,m,q,u,v,t;

     scanf("%lld%lld%lld%lld%lld%lld",&n,&m,&q,&u,&v,&t);

     for(register ll i=;i<=n;++i){

         scanf("%lld",&a[i]);

     }

     sort(a+,a++n,cmp);

     ll ha=,ta=n,hx=,hd=,tx=,td=;

     ll js=,ad=;

     ll mm=m;

     while(mm--){

         js++;

         ll ans=-0x3f3f3f3f3f3f3f3f;

         if(ha<=ta && a[ha]>=ans) ans=a[ha];

         if(hx<=tx && xi[hx]>=ans) ans=xi[hx];

         if(hd<=td && da[hd]>=ans) ans=da[hd];

         if(a[ha]==ans && ha<=ta) ha++;

         else if(xi[hx]==ans && hx<=tx) hx++;

         else hd++;

         ans+=ad;

         if(js%t==) printf("%lld ",ans);

         ll left=u*ans/v;

         ll right=ans-left;

         ad=js*q;

         left-=ad,right-=ad;

         xi[++tx]=min(left,right);

         da[++td]=max(left,right);

     }

     printf("\n");

     ll now=n+m;

     for(ll i=;i<=now;++i){

         ll ans=-0x3f3f3f3f3f3f3f3f;

         if(ha<=ta && a[ha]>=ans) ans=a[ha];

         if(hx<=tx && xi[hx]>=ans) ans=xi[hx];

         if(hd<=td && da[hd]>=ans) ans=da[hd];

         if(a[ha]==ans && ha<=ta) ha++;

         else if(xi[hx]==ans && hx<=tx) hx++;

         else hd++;

         if(i%t==) printf("%lld ",ans+ad);

     }

     printf("\n");

     return ;

 }

这样的话，我们交到洛谷上可以过，但是在Vjudge上会T掉

于是，我又加上了读入优化、输出优化，以及register、inline等等，但发现还是会T

就像上面这样

后来我发现，其实没有必要写额外的读入优化、输出优化

一开始，我为了不炸int，把所有的变量都开成了long long

但实际上，有很多变量只用int就能解决，而且int比long long要快

只要把不必要的long long改成int就可以AC了

代码

 #include<cstdio>

 #include<cstring>

 #include<algorithm>

 #include<iostream>

 #include<queue>

 using namespace std;

 #define maxn 7000005

 #define ll long long

 int a[maxn];

 ll xi[maxn],da[maxn];

 int cmp(int aa,int bb){ return aa>bb; }

 int main(){

     int n,m,q,u,v,t;

     scanf("%d%d%d%d%d%d",&n,&m,&q,&u,&v,&t);

     for(int i=;i<=n;++i){

         scanf("%d",&a[i]);

     }

     sort(a+,a++n,cmp);

     int ha=,ta=n,hx=,hd=,tx=,td=;

     ll js=,ad=;

     int mm=m;

     while(mm--){

         js++;

         ll ans=-0x3f3f3f3f3f3f3f3f;

         if(ha<=ta && a[ha]>=ans) ans=a[ha];

         if(hx<=tx && xi[hx]>=ans) ans=xi[hx];

         if(hd<=td && da[hd]>=ans) ans=da[hd];

         if(a[ha]==ans && ha<=ta) ha++;

         else if(xi[hx]==ans && hx<=tx) hx++;

         else hd++;

         ans+=ad;

         if(js%t==) printf("%lld ",ans);

         ll left=u*ans/v;

         ll right=ans-left;

         ad=js*q;

         left-=ad,right-=ad;

         xi[++tx]=min(left,right);

         da[++td]=max(left,right);

     }

     printf("\n");

     int now=n+m;

     for(int i=;i<=now;++i){

         ll ans=-0x3f3f3f3f3f3f3f3f;

         if(ha<=ta && a[ha]>=ans) ans=a[ha];

         if(hx<=tx && xi[hx]>=ans) ans=xi[hx];

         if(hd<=td && da[hd]>=ans) ans=da[hd];

         if(a[ha]==ans && ha<=ta) ha++;

         else if(xi[hx]==ans && hx<=tx) hx++;

         else hd++;

         if(i%t==) printf("%lld ",ans+ad);

     }

     printf("\n");

     return ;

 }