dfs和bfs的区别

详见转载博客：https://www.cnblogs.com/wzl19981116/p/9397203.html

1.dfs(深度优先搜索)是两个搜索中先理解并使用的，其实就是暴力把所有的路径都搜索出来，它运用了回溯，保存这次的位置，深入搜索，都搜索完了便回溯回来，搜下一个位置，直到把所有最深位置都搜一遍，要注意的一点是，搜索的时候有记录走过的位置，标记完后可能要改回来；

回溯法是一种搜索法，按条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法；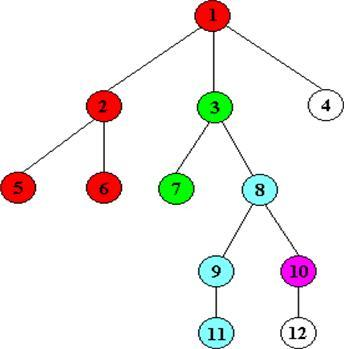

例如这张图，从1开始到2，之后到5，5不能再走了，退回2，到6，退回2退回1，到3，一直进行；

理解这种方法比较简单，难的是要怎么用

void dfs(int deep)
{
    int x=deep/n,y=deep%n;
    if(符合某种要求||已经不能在搜了)
    {
        做一些操作；
        return ;
    }
    if(符合某种条件且有地方可以继续搜索的)//这里可能会有多种条件，可能要循环什么的
    {
        a[x][y]='x';//可能要改变条件，这个是瞎写的
            dfs(deep+,sum+);//搜索下一层
        a[x][y]='.';//可能要改回条件，有些可能不用改比如搜地图上有多少块连续的东西
    }
}

2.bfs(宽度/广度优先搜索)，这个一直理解了思想，不会用，后面才会的，思想，从某点开始，走四面可以走的路，然后在从这些路，在找可以走的路，直到最先找到符合条件的，这个运用需要用到队列(queue)，需要稍微掌握这个才能用bfs。

一张图，bfs就是和它类似，很好的帮助理解，雷从上往下，同时向四面八方的延长（当然不是很严谨的），然后找到那个最近的建筑物，然后劈了它；

还是这张图，从1开始搜，有2，3，4几个点，存起来，从2开始有5，6，存起来，搜3，有7，8，存起来，搜4，没有了；现在开始搜刚刚存的点，从5开始，没有，然后搜6.。。一直进行，直到找到；

int visit[N][N]//用来记录走过的位置
int dir[][]={,-,,,-,,,};
struct node
{
    int x,y,bits;//一般是点，还有步数，也可以存其他的
};
queue<node>v;
void bfs1(node p)
{
    node t,tt;
    v.push(p);
    while(!v.empty())
    {
        t=v.front();//取出最前面的
        v.pop();//删除
        if(找到符合条件的)
        {
            做记录；
            while(!v.empty()) v.pop();//如果后面还需要用，随手清空队列
            return;
        }
        visit[t.x][t.y]=;//走过的进行标记，以免重复
        rep(i,,)//做多次查找
        {
            tt=t;
            tt.x+=dir[i][];tt.y+=dir[i][];//这里的例子是向上下左右查找的
            if(如果这个位置符合条件)
            {
                tt.bits++;//步数加一
                v.push(tt); //把它推入队列，在后面的时候就可以用了
            }
        }
    }
}

3.dfs和bfs的区别

其实有时候两个都可以用，不过需要其他的东西来记录什么的，各自有各自的优势

bfs是用来搜索最短径路的解是比较合适的，比如求最少步数的解，最少交换次数的解，因为bfs搜索过程中遇到的解一定是离最初位置最近的，所以遇到一个解，一定就是最优解，此时搜索算法可以终止，而如果用dfs，会搜一些其他的位置，需要搜很多次，然后还要一个东西来记录这次找的位置，之后找到的还要和这次找到的进行比较，这样就比较麻烦

dfs合搜索全部的解，因为要搜索全部的解，在记录路径的时候也会简单一点，而bfs搜索过程中，遇到离根最近的解，并没有什么用，也必须遍历完整棵搜索树。

dfs是舍弃时间换取空间，bfs是舍去空间换取时间。因为dfs要走很多的路径，可能都是没用的，（做有些题目的时候要进行剪枝，就是确定不符合条件的就可以推出，以免浪费时间，否则有些题目会TLE）；而bfs可以走的点要存起来，需要队列，因此需要空间来储存，但是快一点。

稍微理解之后就可以了，不一定要纠结怎么用，先去做题目，很多都是做着就突然明白怎么用了。