poj 1177 --- Picture(线段树+扫描线 求矩形并的周长)

题目链接

Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.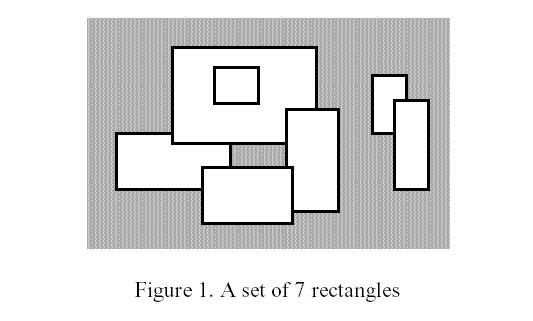 

The corresponding boundary is the whole set of line segments drawn in Figure 2.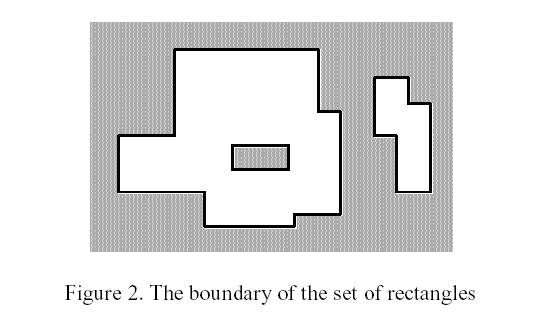 

The vertices of all rectangles have integer coordinates. 

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.

0 <= number of rectangles < 5000 
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

Sample Input

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

Sample Output

228

Source

IOI 1998

 

题意：有多个矩形，矩形的两边平行于坐标轴，这些矩形之间可能存在相互覆盖，求周长。

 

思路：记录每个矩形的两条竖边（x1，y1，y2）和（x2，y1，y2），将所有的竖边按照x从小到大排序，然后一条一条竖边开始计算周长，那么以竖边所在的垂直于x轴的直线即是扫描线。每次移动到一条新的竖边的时候，我们需要计算所在竖边扫描线上有用边长（即当前竖边的有用部分，可能当前的竖边被覆盖部分），以及加上当前扫描线与上一条扫描线之前的横边长 * 横边条数，一直计算到最后一条竖边，即是完整周长了。

 

代码如下：

 #include <iostream>
 #include <algorithm>
 #include <cstdio>
 #include <cstring>
 #include <vector>
 using namespace std;
 const int N=;
 struct Line{
     int x,y1,y2;
     int flag;
     bool operator<(const Line s)
     {
         if(x==s.x) return flag>s.flag;
         return x<s.x;
     }
 }line[N*];

 struct Tree
 {
     int l,r;
     bool lf,rf;  ///左右边界点是否被覆盖;
     int cover_len;
     int cover_num;
     int num;     ///矩形数目;
 }tr[N*];

 vector<int>v;

 void build(int l,int r,int i)
 {
     tr[i].l=l; tr[i].r=r;
     tr[i].cover_len=;
     tr[i].cover_num=;
     tr[i].num=;
     tr[i].lf=tr[i].rf=false;
     if(l+==r) return ;
     int mid=(l+r)>>;
     build(l,mid,i<<);
     build(mid,r,i<<|);
 }
 void process(int i)
 {
     if(tr[i].cover_num>)
     {
         tr[i].cover_len=v[tr[i].r]-v[tr[i].l];
         tr[i].lf=tr[i].rf=true;
         tr[i].num=;
         return ;
     }
     if(tr[i].l+==tr[i].r)
     {
         tr[i].cover_len=;
         tr[i].num=;
         tr[i].lf=tr[i].rf=false;
         return ;
     }
     int ls=(i<<);
     int rs=(i<<|);
     tr[i].cover_len=tr[ls].cover_len+tr[rs].cover_len;
     tr[i].num=tr[ls].num + tr[rs].num - (tr[ls].rf & tr[rs].lf);
     tr[i].lf=tr[ls].lf; tr[i].rf=tr[rs].rf;
 }
 void update(int i,Line t)
 {
     if(t.y1<=v[tr[i].l] && v[tr[i].r]<=t.y2)
     {
         tr[i].cover_num+=t.flag;
         process(i);
         return ;
     }
     int mid=(tr[i].l+tr[i].r)>>;
     if(t.y1<v[mid]) update(i<<,t);
     if(t.y2>v[mid]) update(i<<|,t);
     process(i);
 }
 int main()
 {
     int n;
     while(scanf("%d",&n)!=EOF)
     {
         v.clear();
         for(int i=;i<n;i++)
         {
             int x1,y1,x2,y2;
             scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
             line[i*].x=x1;   line[i*].y1=y1;   line[i*].y2=y2;   line[i*].flag=;
             line[i*+].x=x2; line[i*+].y1=y1; line[i*+].y2=y2; line[i*+].flag=-;
             v.push_back(y1);
             v.push_back(y2);
         }
         sort(line,line+*n);
         sort(v.begin(),v.end());
         int num=unique(v.begin(),v.end())-v.begin();

         build(,num-,);
         int ans=,len=;
         for(int i=;i<*n;i++)
         {
             if(i>) ans+=tr[].num**(line[i].x-line[i-].x);
             update(,line[i]);
             ans+=abs(tr[].cover_len-len);
             len=tr[].cover_len;
         }
         printf("%d\n",ans);
     }
     return ;
 }