Matting任务里的Gradient与Connectivity指标

主要背景

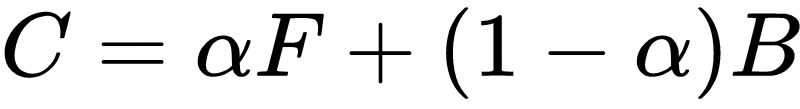
Matting任务就是把α(不透明度, 也就是像素属于前景的概率)、F(前景色)和B(背景色)三个变量给解出来.

C为图像当前可观察到的颜色, 这是已知的. 问题是一个等式解不出三个变量, 因此就必须引入额外的约束使这个方程可解, 这个额外的约束就是由用户指定的trimap(有人译为三元图)图, 或者是仅仅在前景和背景画几笔的草图(scribbles).

主要的手段

传统方法: Poisson Matting/Bayes Matting/Closed Form Matting/KNN Matting
- Color sampling方法, 以Bayesian Matting为代表, 通过对前景和背景的颜色采样构建高斯混合模型, 但是这种方法需
  要高质量的trimap, 不易获取
- Propagation的方法, 根据像素亲和度将用户绘制的信息传播到不确定像素, 以Poisson Matting和KNN matting为代
  表, 但是也不是自动抠图
CNN方法:
- Natural Image Matting Using Deep CNN(ECCV 2016)
- Deep Automatic Portrait Matting(ECCV 2016)
- Automatic Portrait Segmentation for Image Stylization(2016)
- Deep Image Matting(CVPR 2017)
- Semantic Human Matting(2018)等

主要评价指标

来自于论文: Christoph Rhemann, Carsten Rother, Jue Wang, Margrit Gelautz, Pushmeet Kohli, Pamela Rott. A Perceptually Motivated Online Benchmark for Image Matting. Conference on Computer Vision and Pattern Recognition (CVPR), June 2009.

Gradient
Connectivity
SAD
MSE

一些相关的术语, 来自参考链接[1]
SAD（Sum of Absolute Difference）= SAE（Sum of Absolute Error)即绝对误差和
SATD（Sum of Absolute Transformed Difference）即hadamard变换后再绝对值求和
SSD（Sum of Squared Difference）= SSE（Sum of Squared Error)即差值的平方和
MAD（Mean Absolute Difference）= MAE（Mean Absolute Error)即平均绝对差值
MSD（Mean Squared Difference）= MSE（Mean Squared Error）即平均平方误差

大致内容

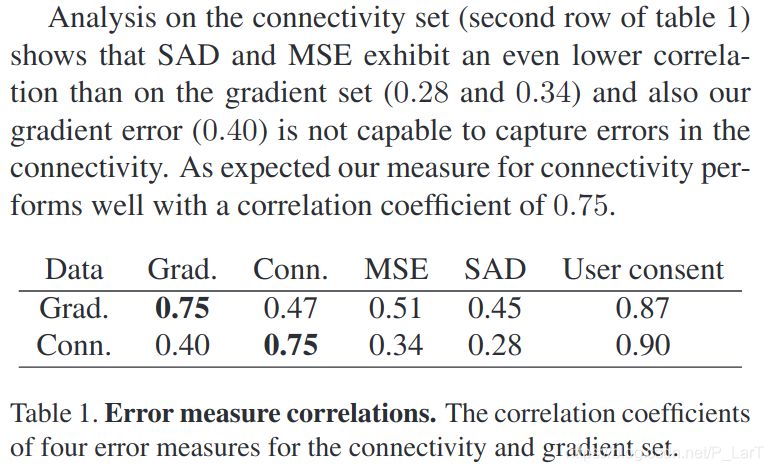
因为若是仅仅考虑SAD和MSE指标, 在和人类判断的对比中, 发现, 并不能很好地反映人类的实际判断标准. 为此文章引入了两个新的指标, 梯度和连通性. 先来说下连通性.

Connectivity

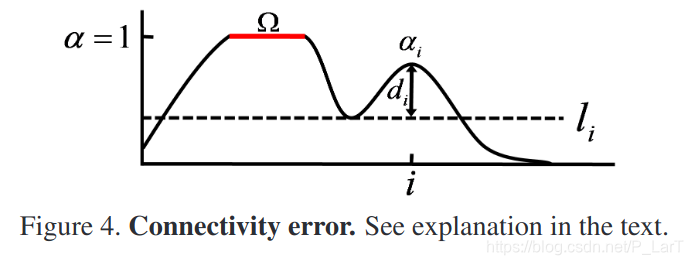
这个图基于matting任务中获得的alpha matte图, 这是一个灰度图, 表示的就是前面的公式里的$\alpha$.

由于这里的图上出现了几个参数, $\alpha_i , \Omega, d_i, l_i, i$, 下面结合具体的公式来理解.

\[
\sum_{i}\left(\varphi\left(\alpha_{i}, \Omega\right)-\varphi\left(\alpha_{i}^{*}, \Omega\right)\right)^{p}
\]

这里的p是自定义参数. 具体见后.

该公式给出了连通性误差的计算方法, 这里是对整个预测出来的alpha matte图和对应的真值的图的对应的差异的累和. 这里的关键是里面的$\varphi\left(\alpha_{i}, \Omega\right)$函数.

首先要解释这里的$\Omega$, 它表示的是对于预测结果图和真值共有的最大的值为1的连通区域, 被称为"源域(source region)", 也就是在上图中红线区域大致表示的范围. 这里的$\varphi$计算的是有着透明度$\alpha_i$的像素i, 与源域的连通度(degree of connectivity), 当其为1则认为该像素与源域全连通, 等于0表示完全不连通. 另一个加星号的表示真值图上的对应像素的连通度的计算. 二者计算差异, 来累计误差. 好的结果应该有着更低的误差, 更相似的连通情况.

公式里的$l_i$表示像素i四连通到源域所需要的最大阈值, 也就是上图中的虚线, 用它对alpha matte进行二值化, 正好处于使像素i与源域连通(实际需要四连通)/不连通的临界. 若是对于一个像素而言, 它的$l=\alpha$, 那么就可以认为它与源域是全连通的.

而公式里的$d_i$如图所示, 表示的就是像素i处的$\alpha$值和对应的临界阈值$l_i$的差距.

\[
\varphi\left(\alpha_{i}, \Omega\right)=1-\left(\lambda_{i} \cdot \delta\left(d_{i} \geq \theta\right) \cdot d_{i}\right)
\]

这里的$\theta$是自定义参数, 具体见后. 它用在指示函数$\delta$里作为一个阈值, 来忽略小于它的$d_i$的情况, 认为小于它就已经是全连通了, 使得误差计算更为灵活.

其中的$\lambda_{i}=\frac{1}{|K|} \sum_{k \in K} dist_{k}(i)$用来对$d_i$进行加权, 这里的K表示$l_i$到$\alpha_i$之间的离散$\alpha$值的集合, $dist_k$计算了设置为阈值$k$时, 对于像素i距离最近的连通到源域的像素, 与像素i之间的标准化欧式距离. 实际情况中, 远离连通区域的像素, 获得的权重$\lambda$也应该相应会更大些, 这样导致得到的$\varphi$会更小些, 也就是认为连通度更小.

Gradient

主要计算的是预测的alpha matte $\alpha$和ground truth $\alpha^{*}$的之间的梯度差异, 定义如下:

\[
\sum_{i}\left(\nabla \alpha_{i}-\nabla \alpha_{i}^{*}\right)^{q}
\]

这里的q是自定义参数. 具体见后

这里的$\nabla \alpha_{i}$和$\nabla \alpha_{i}^{*}$表示的是对应的alpha matte的归一化梯度, 这是通过将matte与具有方差$σ$的一阶Gaussian导数滤波器进行卷积计算得到的. 二者计算差异, 进而累计损失. 总体越相似, 指标值越小.

这里的方差$σ$也是自定义参数, 具体见后

关于参数的选择

对于这里存在四个需要人工设置的参数: $\theta, p, q$, 在参考文章3中, 有进一步的测试与设定, 文章最终选择了这样的设定: $\sigma=1.4, q=2, \theta=0.15, p=1$.

参考文章

https://zhidao.baidu.com/question/1701594942558730300.html
http://alphamatting.com/index.html
Christoph Rhemann, Carsten Rother, Jue Wang, Margrit Gelautz, Pushmeet Kohli, Pamela Rott. A Perceptually Motivated Online Benchmark for Image Matting. Conference on Computer Vision and Pattern Recognition (CVPR), June 2009.`