STL——heap结构及算法

heap（隐式表述，implicit representation）

1. heap概述 : vector + heap算法

heap并不归属于STL容器组件，它是个幕后英雄，扮演priority queue的助手。顾名思义，priority queue允许用户以任何次序将任何元素推入容器内，但取出时一定是从优先权最高（也就是数值最高）的元素开始取。binary max heap 正是具有这样的特性，适合作为priority queue 的底层机制。

让我们做一点分析。如果使用list 作为priority queue的底层机制，元素出入操作可享常数时间。但是要找到list中的极值，却需要对整个list进行线性扫描。我们也可以改变做法，让元素插入前先经过排序，使得list的元素值总是由小到大（或由大到小），但这么一来，收之东隅却失之桑榆：虽然取得极值以及元素删除操作达到最高效率，可元素的插入却只有线性表现。

比较好的做法是以binary search tree 作为priority queue的底层机制。这么一来，元素的插入和极值的取得就有O(logN) 的表现。但杀鸡用牛刀，未免小题大做，一来binary search tree 的输入需要足够的随机性，二来binary search tree并不容易实现。priority queue 的复杂度，最好介于queue 和 binary search tree 之间，才算适得其所。bianry heap便是这种条件下的适当候选人。

所谓binary heap 就是一种complete binary tree（完全二叉树），也就是说，整棵binary tree 除了最底层的叶节点之外，是填满的，而最底层的叶节点(s)由左至右又不得有空隙。

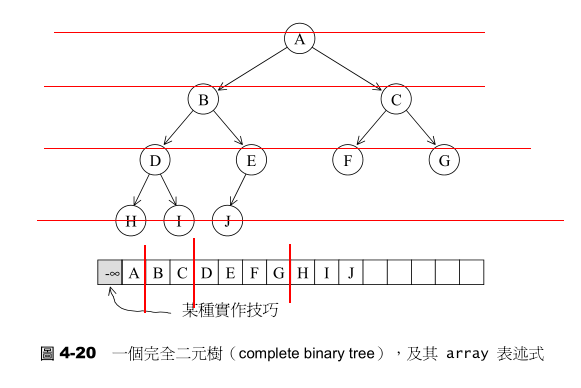
complete binary tree 整棵树内没有任何节点漏洞，这带来一个极大的好处：我们可以利用array来存储所有节点。假设动用一个小技巧，将array的#0元素保留（或设为无限大或无限小），那么当complete binary tree中的某个节点位于array的i处时，其左子节点必位于array的2i处，其右子节点比位于array的2i+1处，其父节点必位于“i/2”处。通过这么简单的位置规则，array可以轻易实现出complete binary tree。这种以array表述tree的方式，我们称为隐式表述法。

这么一来，我们需要的工具就很简单了：一个array 和 一组 heap算法（用来进行元素操作，并将某一整组数据排列成一个heap）。array的缺点是无法动态改变大小，而heap却需要这项功能，因此，以vector代替array是更好的选择。

根据元素的排列方式，heap可分为max-heap 和 min-heap两种，前者每个节点的键值（key）都大于或等于其子节点键值，后者的每个节点键值都小于或等于其子节点键值。STL提供的是max-heap。

2. heap算法

2.1 push_heap算法：上溯

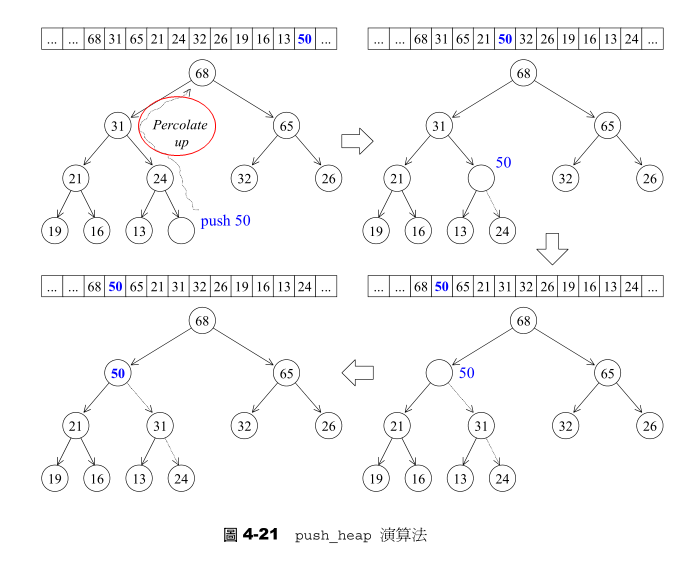
percolate_up（上溯）程序：将新节点拿来与其父节点比较，如果其键值（key）比父节点大，就父子对换位置。如此一直上溯，直到不需对换或直到根节点为止。

push_heap算法的实现细节参见相关源码。

注意：

（1）为了满足complete binary tree的条件，新加入的元素一定要放在最下一层作为叶节点，便填补在由左至右的第一个空格，也就是把新元素插入在底层vector的end()处。

（2）当push_heap函数被调用时，新元素应已置于底部容器的最尾端。

另： array无法动态改变大小，因此如果heap底层采用array，便不可以对满载的array进行push_heap操作，因为那得先在array尾端增加一个元素。如果对一个满载的array执行push_heap，该函数会将最后一个元素视为新增元素，并将其余元素视为一个完整的heap结构（实际上它们的确是），因此执行后的结果等于原先的heap。

2.2 pop_heap算法：下溯+上溯

下图是 pop_heap算法的实际操演情况。既然身为max-heap，最大值必然在根节点。pop操作取走根节点（其实是设至底部容器vector的尾端节点）后，为了满足complete binary tree的条件，必须割舍最下层最右边的叶节点，并将其值重新安插至max-heap（因此有必要重新调整heap结构）。

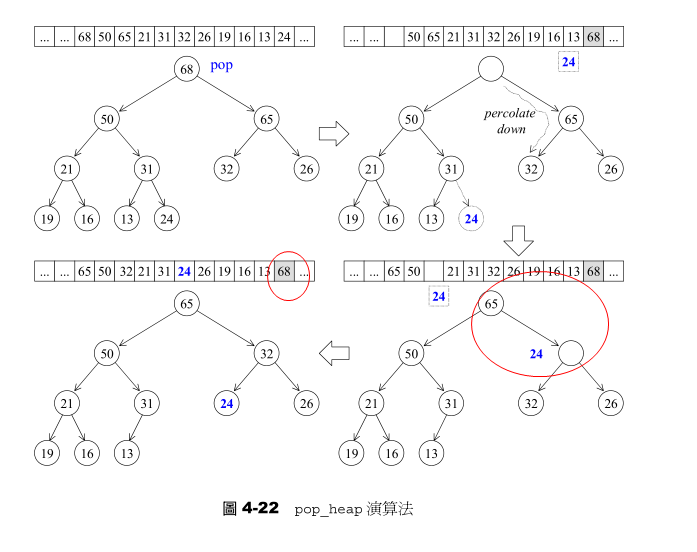
为了满足max-heap次序特性（每个节点的键值都大于或等于其子节点键值），我们执行所谓的percolate down（下溯）程序：将空间节点和其较大子节点“对调”，并持续下放，直至叶节点为止。然后将前述被割舍之元素值设给这个“已到达叶层的空间节点”，再对它执行一次percolate up（上溯）程序。

pop_heap算法的实现细节参见相关源码。

注意：

pop_heap之后，最大元素只是被置于底部容器的最尾端，尚未被取走。

2.3 sort_heap算法

既然每次pop_heap可获得heap中键值最大的元素，如果持续对整个heap做pop_heap操作，每次将操作范围从后向前缩减一个元素（因为pop_heap会把键值最大的元素放在底部容器的最尾端），当整个程序执行完毕时，我们便有了一个递增序列。

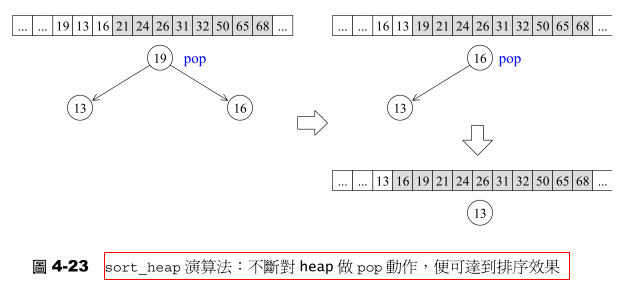
2.4 make_heap算法

这个算法用来将一段现有的数据转化为一个heap。

make_heap算法实现参见相关源码

3. heap没有迭代器 heap的所有元素都必须遵循特别的（complete binary tree）排列规则，所以heap不提供遍历功能，也不提供迭代器。