最小二乘法 及 梯度下降法 运行结果对比(Python版)
上周在实验室里师姐说了这么一个问题,对于线性回归问题,最小二乘法和梯度下降方法所求得的权重值是一致的,对此我颇有不同观点。如果说这两个解决问题的方法的等价性的确可以根据数学公式来证明,但是很明显的这个说法是否真正的成立其实很有其它的一些考虑因素在里面,以下给出我个人的一些观点:
1. 首先,在讨论最小二乘法和梯度下降对某数据集进行线性拟合的结果是否相同的问题之前,我们应该需要确保该数据集合的确符合线性模型,如果不符合那么得出的结果将会是非常有意思的,
该种情况在之前的博客中已有介绍,下面给出网址:http://www.cnblogs.com/devilmaycry812839668/p/7704729.html
2. 再者, 在讨论二者结果是否相同的问题之前如果对梯度下降法做过实际编码的人员一定知道这么一个东西,那就是步长,即每次对权重进行修正时的权重配比。虽然对于凸优化问题对初始点不敏感,但是步长的设置却会影响最终收敛时权重的精度,甚至造成权值震荡的想象发生,以下给出具体实验代码及结果:
最小二乘法:
#!/usr/bin/env python
#encoding:UTF-8
import numpy as np
import matplotlib.pyplot as plt np.random.seed(0) N=10
X=np.linspace(-3, 3, N)
Z=-5.0+X+np.random.random(N) P=np.ones((N, 1))
P=np.c_[P, X] t=np.linalg.pinv(P)
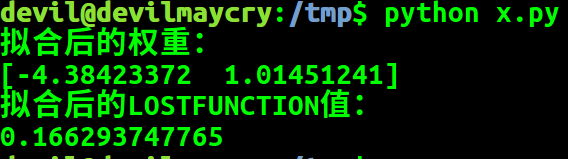
w=np.dot(t, Z) print "拟合后的权重:"
print w
A=np.dot(P, w)-Z print "拟合后的LOSTFUNCTION值:"
print np.dot(A, A)/2
结果:
梯度下降法:
#!/usr/bin/env python
#encoding:UTF-8
import numpy as np
import matplotlib.pyplot as plt np.random.seed(0) N=10 X=np.linspace(-3, 3, N)
Z=-5+X+np.random.random(N) P=np.ones((N, 1))
P=np.c_[P, X] alafa=0.001 def fun():
W=np.random.random(2) for _ in xrange(1000000000):
A=(np.dot(P, W)-Z) W0=alafa*( np.sum(A) )
W1=alafa*( np.dot(A, X) ) if abs(W0)+abs(W1)<0.000001:
break W[0]=W[0]-W0
W[1]=W[1]-W1 return W list_global=[]
for _ in xrange(100):
list_global.append( fun() )
list_global.sort(key=lambda x:x[0])
for k in list_global:
print k
结果:
[-4.38413472 1.01451241]
[-4.38413469 1.01451241]
[-4.38413469 1.01451241]
[-4.38413468 1.01451241]
[-4.38413468 1.01451241]
[-4.38413464 1.01451241]
[-4.38413463 1.01451241]
[-4.38413461 1.01451241]
[-4.38413461 1.01451241]
[-4.3841346 1.01451241]
[-4.38413459 1.01451241]
[-4.38413458 1.01451241]
[-4.38413457 1.01451241]
[-4.38413457 1.01451241]
[-4.38413457 1.01451241]
[-4.38413455 1.01451241]
[-4.38413454 1.01451241]
[-4.38413451 1.01451241]
[-4.38413446 1.01451241]
[-4.38413444 1.01451241]
[-4.38413444 1.01451241]
......
......
......
由梯度下降法可知,由于初始点的不同最终的优化结果稍有差异,但是考虑精度的情况下可以认为所有结果均为一致,此时是支持学姐的说法的。
若改变步长大小,即
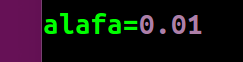
可得结果:
[-4.3842247 1.01451241]
[-4.38422468 1.01451241]
[-4.38422468 1.01451241]
[-4.38422467 1.01451241]
[-4.38422465 1.01451241]
[-4.38422464 1.01451241]
[-4.3842246 1.01451241]
[-4.38422459 1.01451241]
[-4.38422458 1.01451241]
[-4.38422457 1.01451241]
[-4.38422455 1.01451241]
[-4.38422455 1.01451241]
[-4.38422453 1.01451241]
[-4.38422452 1.01451241]
[-4.38422452 1.01451241]
[-4.38422452 1.01451241]
[-4.38422451 1.01451241]
[-4.3842245 1.01451241]
.........
........
........
此时,运行结果和上个实验的运行结果稍有不同,可以发现该种差异源于步长大小的设置上,也就是说步长的大小不同导致了最终结果的精确度不同。
这次,我们再次改变步长大小,此时运行的结果并没有出来,可以说上面的程序在该步长下是无法运行出结果的,下面做下修改:
#!/usr/bin/env python
#encoding:UTF-8
import numpy as np
import matplotlib.pyplot as plt np.random.seed(0) N=10 X=np.linspace(-3, 3, N)
Z=-5+X+np.random.random(N) P=np.ones((N, 1))
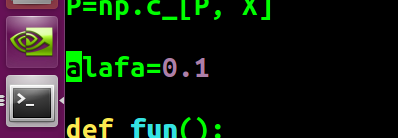
P=np.c_[P, X] alafa=0.1 def fun():
W=np.random.random(2) for _ in xrange(100):
A=(np.dot(P, W)-Z) W0=alafa*( np.sum(A) )
W1=alafa*( np.dot(A, X) ) W[0]=W[0]-W0
W[1]=W[1]-W1 print W fun()
运行结果,如下:
[-4.38423372 2.30949239]
[-4.38423372 -2.43876754]
[ -4.38423372 10.22325895]
[ -4.38423372 -23.54214502]
[ -4.38423372 66.49893222]
[ -4.38423372 -173.61060709]
[ -4.38423372 466.68149774]
[ -4.38423372 -1240.76411513]
[ -4.38423372 3312.42418586]
[ -4.38423372e+00 -8.82941128e+03]
[ -4.38423372e+00 2.35488166e+04]
[ -4.38423372e+00 -6.27931245e+04]
[ -4.38423372e+00 1.67452052e+05]
[ -4.38423372e+00 -4.46535085e+05]
[ -4.38423372e+00 1.19076395e+06]
[ -4.38423372e+00 -3.17536680e+06]
[ -4.38423372e+00 8.46764853e+06]
[ -4.38423371e+00 -2.25803924e+07]
[ -4.38423372e+00 6.02143834e+07]
[ -4.38423371e+00 -1.60571685e+08]
[ -4.38423375e+00 4.28191164e+08]
[ -4.38423373e+00 -1.14184310e+09]
.......
.......
.......
[ -2.14824842e+17 2.17682829e+33]
[ 1.31051609e+17 -5.80487543e+33]
[ -7.91285594e+17 1.54796678e+34]
[ 1.97572602e+18 -4.12791142e+34]
[ -3.55829721e+18 1.10077638e+35]
[ 1.11990981e+19 -2.93540367e+35]
[ -3.30730877e+19 7.82774313e+35]
[ 5.54712838e+19 -2.08739817e+36]
[ -4.16765364e+20 5.56639512e+36]
[ 2.91589608e+20 -1.48437203e+37]
[ 2.91589608e+20 3.95832542e+37]
[ 5.95842939e+21 -1.05555344e+38]
[ -5.37525017e+21 2.81480918e+38]
[ 2.48478953e+22 -7.50615783e+38]
[ -6.58215412e+22 2.00164209e+39]
[ 4.17748787e+23 -5.33771223e+39]
[ -7.91177033e+23 1.42338993e+40]
[ 1.14310428e+24 -3.79570648e+40]
[ -2.72545834e+24 1.01218839e+41]
[ 5.01166690e+24 -2.69916905e+41]
[ -2.59368341e+25 7.19778413e+41]
[ 3.59601679e+25 -1.91940910e+42]
可见,其权重值是发散的,并不断震荡。
再次更改步长,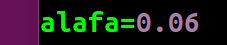
运行结果:
[-2.31385021 1.5972534 ]
[-3.55608032 0.31522322]
[-4.05297236 1.85365944]
[-4.25172917 0.00753598]
[-4.3312319 2.22288413]
[-4.36303299 -0.43553365]
[-4.37575343 2.75456769]
[-4.3808416 -1.07355392]
[-4.38287687 3.52019201]
[-4.38369098 -1.99230311]
[-4.38401662 4.62269104]
[-4.38414688 -3.31530194]
[-4.38419898 6.21028963]
[-4.38421982 -5.22042025]
[-4.38422816 8.49643161]
[-4.38423149 -7.96379062]
[ -4.38423283 11.78847605]
[ -4.38423336 -11.91424395]
[ -4.38423357 16.52902005]
[ -4.38423366 -17.60289675]
[ -4.38423369 23.35540341]
[ -4.38423371 -25.79455679]
[ -4.38423371 33.18539545]
[ -4.38423372 -37.59054724]
[ -4.38423372 47.34058399]
[ -4.38423372 -54.57677348]
............
............
............
[ -4.38423372e+00 2.61036000e+06]
[ -4.38423372e+00 -3.13242977e+06]
[ -4.38423372e+00 3.75891795e+06]
[ -4.38423372e+00 -4.51069931e+06]
[ -4.38423372e+00 5.41284140e+06]
[ -4.38423372e+00 -6.49540745e+06]
[ -4.38423372e+00 7.79449117e+06]
[ -4.38423372e+00 -9.35338718e+06]
[ -4.38423372e+00 1.12240668e+07]
[ -4.38423372e+00 -1.34688780e+07]
[ -4.38423372e+00 1.61626558e+07]
[ -4.38423372e+00 -1.93951847e+07]
[ -4.38423372e+00 2.32742239e+07]
[ -4.38423371e+00 -2.79290665e+07]
[ -4.38423372e+00 3.35148820e+07]
[ -4.38423371e+00 -4.02178562e+07]
可以,看到该种步长下,常数项权重收敛,X项权重仍然震荡。
由此,可以看出 对于 最小二乘 及 梯度下降 能否得到 相同权重结果 还是蛮有讨论的一个问题。
==============================================================
对于,梯度下降 权重震荡的附加一个解释:
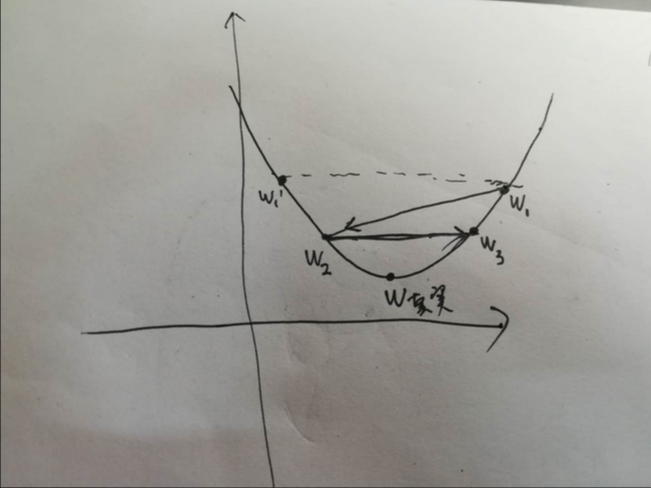
在梯度下降问题中,如上图所示,W为权重的真实值,W1 为梯度下降过程中对真实值的估计,在此之前所有权重的估计值(即,历史估计的值,或者说迭代过程中在对真实值进行逼近的过程中)所取得的所有值均在真实值的一侧, W2为首次估计值越过真实值到达另一侧的权重值, W’ 为W1关于真实值在其另一侧的对称值,如果W2比W’ 更靠近真实值,则下一次的权重估计值 W3 必然比 W1 更逼近真实值。此时,为收敛的。该种情况下说明步长的选择可以使权重收敛。
如果,W2 比 W’ 要远离真实值,则W3 必然比 W1 相比要远离真实值W。此时,权重的估计是发散的。
具体示意图如下: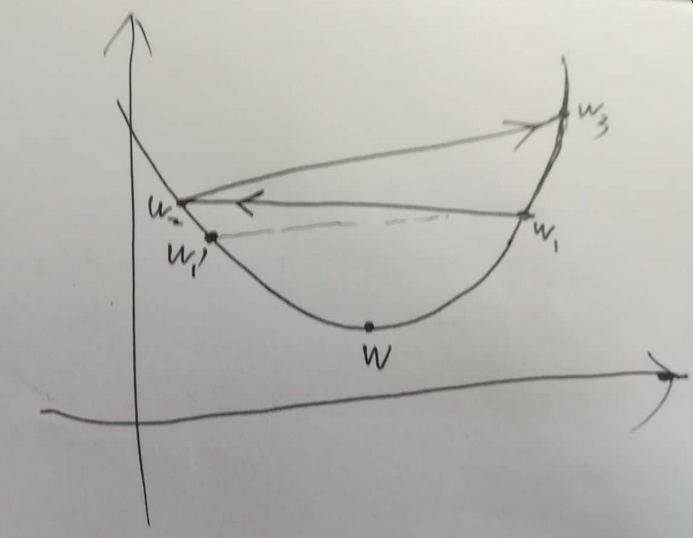
最小二乘法 及 梯度下降法 运行结果对比(Python版)的更多相关文章
- 最小二乘法 及 梯度下降法 分别对存在多重共线性数据集 进行线性回归 (Python版)
网上对于线性回归的讲解已经很多,这里不再对此概念进行重复,本博客是作者在听吴恩达ML课程时候偶然突发想法,做了两个小实验,第一个实验是采用最小二乘法对数据进行拟合, 第二个实验是采用梯度下降方法对数据 ...
- [DeeplearningAI笔记]改善深层神经网络_优化算法2.1_2.2_mini-batch梯度下降法
觉得有用的话,欢迎一起讨论相互学习~Follow Me 2.1 mini-batch gradient descent mini-batch梯度下降法 我们将训练数据组合到一个大的矩阵中 \(X=\b ...
- (转)梯度下降法及其Python实现
梯度下降法(gradient descent),又名最速下降法(steepest descent)是求解无约束最优化问题最常用的方法,它是一种迭代方法,每一步主要的操作是求解目标函数的梯度向量,将当前 ...
- 机器学习---用python实现最小二乘线性回归算法并用随机梯度下降法求解 (Machine Learning Least Squares Linear Regression Application SGD)
在<机器学习---线性回归(Machine Learning Linear Regression)>一文中,我们主要介绍了最小二乘线性回归算法以及简单地介绍了梯度下降法.现在,让我们来实践 ...
- 固定学习率梯度下降法的Python实现方案
应用场景 优化算法经常被使用在各种组合优化问题中.我们可以假定待优化的函数对象\(f(x)\)是一个黑盒,我们可以给这个黑盒输入一些参数\(x_0, x_1, ...\),然后这个黑盒会给我们返回其计 ...
- 梯度下降法VS随机梯度下降法 (Python的实现)
# -*- coding: cp936 -*- import numpy as np from scipy import stats import matplotlib.pyplot as plt # ...
- 梯度下降法原理与python实现
梯度下降法(Gradient descent)是一个一阶最优化算法,通常也称为最速下降法. 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离 ...
- 梯度下降法实现-python[转载]
转自:https://www.jianshu.com/p/c7e642877b0e 梯度下降法,思想及代码解读. import numpy as np # Size of the points dat ...
- 线性回归(最小二乘法、批量梯度下降法、随机梯度下降法、局部加权线性回归) C++
We turn next to the task of finding a weight vector w which minimizes the chosen function E(w). Beca ...
随机推荐
- 快速幂模n运算
模运算里的求幂运算,比如 5^596 mod 1234, 当然,直接使用暴力循环也未尝不可,在书上看到一个快速模幂算法 大概思路是,a^b mod n ,先将b转换成二进制,然后从最高位开始(最高位一 ...
- MS SQL动态创建临时表
开发业务需求,需要对一个表作数据分析,由于数据量较大,而且分析时字段会随条件相应变化而变化. 因此计划先把数据转插入一个临时表,再对临时表的数据进行分析. 问题点是如何动态创建临时表.原先Insus. ...
- 《剑指offer》第十三题(机器人的运动范围)
// 面试题:机器人的运动范围 // 题目:地上有一个m行n列的方格.一个机器人从坐标(0, 0)的格子开始移动,它 // 每一次可以向左.右.上.下移动一格,但不能进入行坐标和列坐标的数位之和 // ...
- boosting方法
概述 Boosting基本思想: 通过改变训练数据的概率分布(训练数据的权值分布),学习多个弱分类器,并将它们线性组合,构成强分类器. Boosting算法要求基学习器能对特定的数据分布进行学习,这可 ...
- 解决Resource doesn't have a corresponding Go package.问题
首先上图 这个报错主要是程序要启动没有入口的原因,package main下边的mian方法才是一个程序的入口.这就要 修改目录结构如下图修改并运行就可以了
- idea运行main方法报错,提示Shorten command line for xxx
在Intell IDEA运行main函数的时候遇到了如下错误: Error running' xxxxxx': Command line is too long. Shorten command li ...
- C#使用xpath查找xml节点信息
Xpath是功能很强大的,但是也是相对比较复杂的一门技术,最好还是到博客园上面去专门找一些专业的帖子来看一看,下面是一些简单的Xpath语法和一个实例,提供给你参考一下. xml示例: <?xm ...
- javascript变量声明及作用域总结
javascript变量声明及作用域总结 一.总结 一句话总结:还是得好好看书,光看视频是不得行的,浅学无用,要相互印证,要真正理解才有用,比如<Javascript权威指南> 书 1.j ...
- 雷林鹏分享:C# 反射(Reflection)
C# 反射(Reflection) 反射(Reflection) 对象用于在运行时获取类型信息.该类位于 System.Reflection 命名空间中,可访问一个正在运行的程序的元数据. Syste ...
- Confluence 6 选项 1 – 在 Confluence 中手动重建用户和用户组
当你只有少量的用户和用户组的时候,使用这个方法. 使用 Confluence 的系统管理员登录 Confluence. 进入用户目录管理界面,然后移动 内部目录(internal directory) ...
