UVa 12627 奇怪的气球膨胀（分治）

https://vjudge.net/problem/UVA-12627

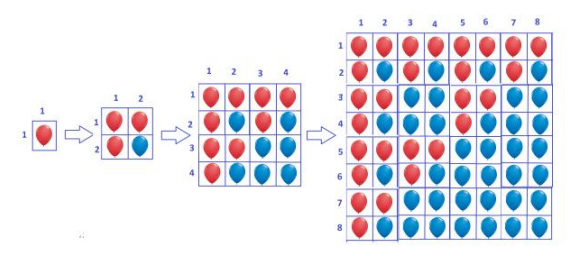
题意：一开始有一个红气球。每小时后，一个红气球会变成3个红气球和1个蓝气球，而1个蓝气球会变成4个蓝气球。如图所示分别是经过0,1,2,3,小时后得情况。经过k小时后，第A~B行一共有多少个红气球。

思路：由图分析，每次把图分为四个部分，右下角的部分全为蓝气球，不用去管他，剩下三部分都是一样的并且和前一小时的图形是一样的，这样的话我们可以计算出每个时刻红气球的总数。

既然每次可以分为四部分，那么很明显的就是用分治法来解决。分别计算出B行之前和A-1行之前的红气球总数，那么A~B行的气球总数就是两者相减。

 #include<iostream>
 using namespace std;

 long long ans[];

 long long f(int k,int i)
 {
     if (i==)     return ;
     if (k==)     return ;
     if (i <  << (k - ))   return  * f(k - , i);
     else return f(k - , i - ( << (k - ))) +  * ans[k - ];
 }

 int main()
 {
     //freopen("D:\\txt.txt", "r", stdin);
     int n;
     cin >> n;
     int k, a, b, kase=;
     ans[] = ;
     for (int i = ; i < ; i++)
     {
         ans[i] =  * ans[i - ];
     }
     for (int i = ; i < n; i++)
     {
         cin >> k >> a >> b;
         long long num = f(k, b) - f(k, a - );
         cout << "Case " << ++kase << ": " << num << endl;
     }
     return ;
 }