LG4455 【[CQOI2018]社交网络】

CQOI2018 社交网络

题目背景

当今社会，在社交网络上看朋友的消息已经成为许多人生活的一部分。通常，一个用户在社交网络上发布一条消息(例如微博、状态、Tweet等) 后，他的好友们也可以看见这条消息，并可能转发。转发的消息还可以继续被人转发，进而扩散到整个社交网络中。

题目描述

在一个实验性的小规模社交网络中我们发现，有时一条热门消息最终会被所有人转发。为了研究这一现象发生的过程，我们希望计算一条消息所有可能的转发途径有多少种。为了编程方便，我们将初始消息发送者编号为1,其他用户编号依次递增。

该社交网络上的所有好友关系是已知的,也就是说对于A、B 两个用户，我们知道A 用户可以看到B 用户发送的消息。注意可能存在单向的好友关系，即lA 能看到B 的消息，但B 不能看到A 的消息。

还有一个假设是，如果某用户看到他的多个好友转发了同一条消息，他只会选择从其中一个转发，最多转发一次消息。从不同好友的转发，被视为不同的情况。

如果用箭头表示好友关系，下图展示了某个社交网络中消息转发的所有可能情况。 (初始消息是用户1发送的，加粗箭头表示一次消息转发)

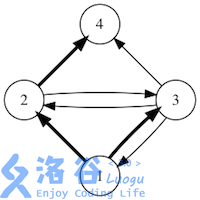
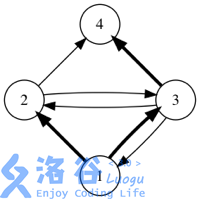
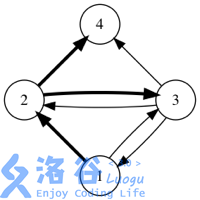
说明

对于30%的数据，$1≤n≤10$

对于100%的数据，$1≤n≤250, 1≤a_i,b_i≤n, 1≤m≤n(n-1)$

题解

求的其实就是有向图中以1为根的生成树数量。Matrix Tree定理裸题。

入度矩阵对应的外向树，出度矩阵对应着内向树（都是指向父亲的边的事是出度或者入度）无根树就是两条有向边都加上

有向树必须删掉根所在的那一行和一列，无根树可以任意

然后对于这n−1阶的矩阵求一个行列式就行了，也叫主子式

#include<bits/stdc++.h>
using namespace std;

void read(int&x) {
	x=0;int w=1;char ch=getchar();
	for(; !isdigit(ch); ch=getchar())if(ch=='-') w=-w;
	for(; isdigit(ch); ch=getchar()) x=x*10+ch-'0';
	x*=w;
}

const int mod=1e4+7;
int fpow(int x,int k) {
	int ans=1;
	for(; k; k>>=1,x=x*x%mod)
		if(k&1) ans=ans*x%mod;
	return ans;
}

int A[255][255];
int gauss(int n) {
	int p=1;
	for(int i=1; i<n; i++) {
		int k=i;
		for(int j=i+1; j<=n; j++)
			if(A[j][i]>A[k][i]) k=j;
		if(k!=i) swap(A[k],A[i]),p*=-1;
		if(!A[i][i])
			return 0;
		int inv=fpow(A[i][i],mod-2);
		for(int j=i+1; j<=n; j++) {
			int coef=A[j][i]*inv%mod;
			for(int k=i; k<=n; k++) A[j][k]=(A[j][k]+mod-coef*A[i][k]%mod)%mod;
		}
	}
	if(p<0) p+=mod;
	for(int i=1; i<=n; i++) p=p*A[i][i]%mod;
	return p;
}
int main() {
	int n,m;
	read(n),read(m);
	for(int x,y; m--;) {
		read(x),read(y); // y->x
		--A[y-1][x-1],++A[x-1][x-1];
	}
	for(int i=0; i<n; i++)for(int j=0; j<n; j++)
		if(A[i][j]<0) A[i][j]+=mod;
	printf("%d\n",gauss(n-1));
	return 0;
}

快速求解行列式

求行列式的一般方法是把矩阵通过基础行变换或者列变换把矩阵消成一个上三角矩阵，然后对角线上的值相乘即可

具体的变换是

1. 行列交换，行列式不变 就是ai,j变成aj,i（但是一般用不上这个）
2. 行列式一行的因子可以提出 就是一行都除k,求完这个行列式后再乘上k
3. 两行互换，行列式反号
4. 将一行的倍数加到另一行上，行列式不变

好像写的话只需要34就够了

黑暗前的幻想乡

幽香上台以后，第一项措施就是要修建幻想乡的公路。幻想乡有 N 个城市，之间原来没有任何路。幽香向选民承诺要减税，所以她打算只修 N- 1 条路将

这些城市连接起来。但是幻想乡有正好 N- 1 个建筑公司，每个建筑公司都想在修路的过程中获得一些好处。

虽然这些建筑公司在选举前没有给幽香钱，幽香还是打算和他们搞好关系，因为她还指望他们帮她建墙。所以她打算让每个建筑公司都负责一条路来修。

每个建筑公司都告诉了幽香自己有能力负责修建的路是哪些城市之间的。所以幽香打算选择 N-1 条能够连接幻想乡所有城市的边，然后每条边都交给一个能够负责该边的建筑公司修建，并且每个建筑公司都恰好修一条边。

幽香现在想要知道一共有多少种可能的方案呢？两个方案不同当且仅当它们要么修的边的集合不同，要么边的分配方式不同。

N<=17

jklover的题解

如果把所有出现的边都加上,直接算生成树个数,可能会包括了有某些公司没有用边的情况.

于是减去 1 个公司不修路,其他公司随便修的方案数.再加上 2 个公司不修路的方案数…

二进制大力枚举每个公司的边考不考虑,用矩阵树定理算方案数,乘上容斥系数即可.

时间复杂度 O(2ⁿ⋅n³) .

#include<bits/stdc++.h>
using namespace std;
template<class T> T read(){
    T x=0,w=1;char c=getchar();
    for(;!isdigit(c);c=getchar())if(c=='-') w=-w;
    for(;isdigit(c);c=getchar()) x=x*10+c-'0';
    return x*w;
}
template<class T> T read(T&x){
    return x=read<T>();
}
#define co const
#define il inline
typedef long long LL;

co int mod=1000000000+7;
il int add(int a,int b){
	return (a+=b)>=mod?a-mod:a;
}
il int mul(int a,int b){
	return (LL)a*b%mod;
}
il int fpow(int a,int b){
	int ans=1;
	for(;b;b>>=1,a=mul(a,a))
		if(b&1) ans=mul(ans,a);
	return ans;
}

co int N=17;
int n;
typedef pair<int,int> edge;
vector<edge> e[N];
int A[N][N];

int gauss(){
	int ans=1;
	for(int i=1;i<n;++i){
		if(!A[i][i]){
			for(int j=i+1;j<n;++j)if(A[j][i]){
				swap(A[i],A[j]),ans=mul(ans,mod-1);
				break;
			}
		}
		if(!A[i][i]) return 0;
		ans=mul(ans,A[i][i]);
		for(int j=i+1;j<n;++j){
			int alph=mul(mod-A[j][i],fpow(A[i][i],mod-2));
			for(int k=i;k<n;++k) A[j][k]=add(A[j][k],mul(alph,A[i][k]));
		}
	}
	return ans;
}
int main(){
	read(n);
	for(int i=0;i<n-1;++i)
		for(int m=read<int>();m--;)
			e[i].push_back((edge){read<int>()-1,read<int>()-1});

	int ans=0;
	for(int s=0;s<1<<(n-1);++s){
		memset(A,0,sizeof A);
		for(int i=0;i<n-1;++i)if(~s>>i&1){
			for(int j=0;j<(int)e[i].size();++j){
				int u=e[i][j].first,v=e[i][j].second;
				++A[u][u],++A[v][v];
				A[u][v]=add(A[u][v],mod-1),A[v][u]=add(A[v][u],mod-1);
			}
		}
		ans=add(ans,__builtin_popcount(s)&1?mod-gauss():gauss());
	}
	printf("%d\n",ans);
	return 0;
}

2019年9月23日10:39:49，LOJ又炸了。