无向图广度优先遍历及其matlab实现

广度优先遍历(breadth-first traverse,bfts)，称作广度优先搜索（breadth first search）是连通图的一种遍历策略。之所以称作广度优先遍历是因为他的思想是从一个顶点V0开始，辐射状地优先遍历其周围较广的区域。

算法描述

给定图G=(V,E)。V是节点集合，E是边集合。

设定一个访问标志位vflag(i)表示节点i的访问情况，若vflag(i)=0表示节点i未被访问

vflag(i)=1表示节点i已经被访问过。

l  初始化所有节点的vflag=0。

l  从图中某个节点V0出发(该节点可以是任意的)，并访问此顶点。

l  从V0出发，访问V0的各个未曾访问的邻接点(下标从小到大排列)W1，W2，…,Wk;然后,依次从W1,W2,…,Wk出发访问各自未被访问的邻接点。

l  重复上步，直到全部顶点都被访问为止。

For example，

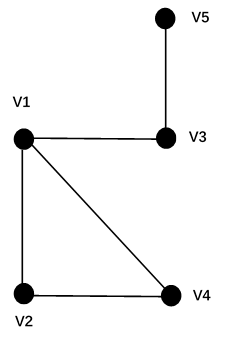
fig1. 5节点无向图

假设我们先从V3 节点开始，把V3装进遍历结果队列和缓存队列。将V3访问标志位置1。取出缓存队列首位后并丢弃。这里是V3节点。找出与V3节点相邻的并未被访问过的节点有。有V1和V5节点，按下标大小我们将V1和V5分别装进缓存队列和遍历队列。自此。缓存队列是[1,5]。遍历队列是[3,1,5]。此时缓存队列没有丢空，我们继续重复之前的步骤。即取出并丢弃缓存队列队首V1。找出与V1相邻并未访问过的节点，有V2,V4.. 此时缓存队列是[5,2,4],遍历队列是[3,1,5,2,4]。此时，已经完成遍历。缓存队列还未被丢空，继续重复上述步骤。即取出并丢弃缓存队列队首V5，找出与V5相邻未被访问的节点，没有。V3相邻但是V3已被访问。此时缓存队列是[2,4],遍历队列是[3,1,5,2,4]。类似丢V2，V4直至缓存队列丢空。实际为节省程序运行时间可将遍历结束条件设为访问标志队列全部非0。

bfst matlab 代码

 %==========================================================================
 % 文件名：        bfstdemo.m
 % 版本号：        1.0.
 % 作者：          Le. <zoreyosa@foxmail.com>
 % 单位：          specter
 % 修改时间：      Sat Oct.  ::
 % 创建时间：      Sat Oct.  ::
 %--------------------------------------------------------------------------
 % blog:http://www.cnblogs.com/athlonreg
 % Copyright (c)  Le. All rights reserved.
 %==========================================================================

 %% 清空环境变量
 close all
 clear all
 clc

 A=[    ;
        ;
        ;
        ;
         ];                  % 输入邻接矩阵
 [m n]=size(A);
 nodeNum=m;                       % 节点数
 vflag=zeros(nodeNum,);          % 初始化所有节点访问标志位
 queue=[];                        % 遍历缓存队列，每次访问并丢弃队首
 result=[];                       % 遍历结果
 startNode=;%unidrnd(nodenum);   % 从任意节点出发
 queue=[queue;startNode];         % 更新遍历缓存队列
 vflag(startNode)=;              % 更新访问标志
 result=[result;startNode];       % 更新遍历结果队列
 % while isempty(queue)==false
 while all(vflag)==
     i=queue();
     queue()=[];
     for j=:n
         if(A(i,j)>&&vflag(j)==&&i~=j)
             queue=[queue;j];
             vflag(j)=;
             result=[result;j];
         end
     end
 end