关路灯，洛谷dp

题目传送门https://www.luogu.org/problem/show?pid=1220

我们假设 dpij0 为目前最优值是在 i 位置,dpij1 为目前最优值是在 j 位置
则 i 到 j 表示已经关掉的灯的区间，因为我们要求最小的损耗，所以必然是从当前区间走向区间两端
再利用前缀和来算从前一个位置走向当前位置所需要的时间，再乘上没关掉电灯的功率即可
for(i = c to 1)for(j = i+1 to n)

dp[i][j][0]=min(dp[i][j][0],dp[i+1][j][0]+(a[i+1]-a[i])*(b[n]-(b[j]-b[i])));//分4情况，耗能计算，时间乘以功率
dp[i][j][0]=min(dp[i][j][0],dp[i+1][j][1]+(a[j]-a[i])*(b[n]-(b[j]-b[i])));
dp[i][j][1]=min(dp[i][j][1],dp[i][j-1][1]+(a[j]-a[j-1])*(b[n]-(b[j-1]-b[i-1])));
dp[i][j][1]=min(dp[i][j][1],dp[i][j-1][0]+(a[j]-a[i])*(b[n]-(b[j-1]-b[i-1])));

至于这个方程怎么推的，请看解释（只推了第一个方程，其他类比）如下，

时间t=a[i+1]-a[i],距离s=b[n]-(b[j]-b[i])(不懂的可以留言哦！！！）

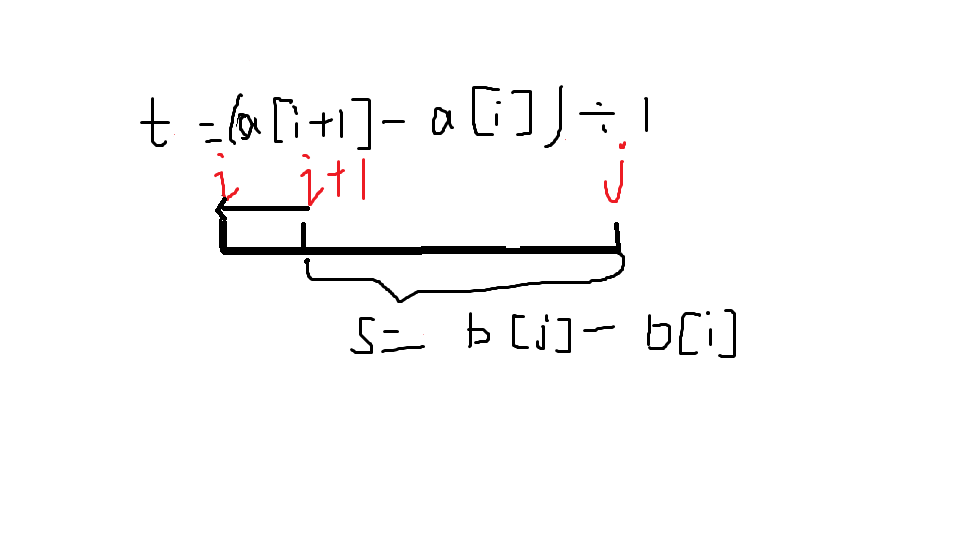
代码

//Gang
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#define FOR(x,y,z) for(int x=y;x<=z;x++)
#define REP(x,y,z) for(int x=y;x>=z;x--)
#define INF 0x3f3f3f3f
#define ll long long
using namespace std;
][][];//dp[i][j][0]表示关掉i to j区间灯后得到最优值在i的位置。//dp[i][j][1]则表示结束后在j的位置
],b[],c,n;//a[i]表示每个路灯的位置，b[i]表示每个路灯的功率
int main()
{
    scanf("%d %d",&n,&c);
    FOR(i,,n)
    {
        scanf("%d %d",&a[i],&b[i]);
        b[i]+=b[i-];
    }
    FOR(i,,n)
    FOR(j,,n)
    dp[i][j][]=dp[i][j][]=INF;//求最小值初值符得很大
    dp[c][c][]=dp[c][c][]=;
    REP(i,c,)
    {
        FOR(j,i+,n)
        {
            dp[i][j][]=min(dp[i][j][],dp[i+][j][]+(a[i+]-a[i])*(b[n]-(b[j]-b[i])));//分4种情况，耗能计算，时间乘以功率
            dp[i][j][]=min(dp[i][j][],dp[i+][j][]+(a[j]-a[i])*(b[n]-(b[j]-b[i])));
            dp[i][j][]=min(dp[i][j][],dp[i][j-][]+(a[j]-a[j-])*(b[n]-(b[j-]-b[i-])));
            dp[i][j][]=min(dp[i][j][],dp[i][j-][]+(a[j]-a[i])*(b[n]-(b[j-]-b[i-])));
        }
    }
    printf(][n][],dp[][n][]));
    ;
}