逆向libbaiduprotect（四）

百度加固libbaiduprotect.so自身对只读字符串进行了加密保护，防止成为破解和逆向的切入口。一般地认为，只要找出这个解密算法就可以对.rodata段的只读字符串进行破解，从而窥探程序的意图。定位解密的位置不难，但是百度使用了多重匹配的手段，有力地加强了难度，因为解密的函数不是一个，而是一组。对于一个字符串只可以被其中一个解密函数解密。如果有M个字符串，N个解密函数，那么就是MxN的组合。首先你要定位出不是一处解密函数，而是N个解密函数，并且N为未知。确定后，有MxN个可能解密的字符串，必须过滤掉Mx(N-1)个不正确的解密字符串。这样还不止，百度加固还使用了另一种手段，使得破解都不在字符串的加密字节流的首字节开始进行的解密失败。

上图的左侧是一段运行中的代码片段，这段代码接踵地调用字符串解密函数，并将解密后的字符串传入下一个函数进行调用。划红线的三处就是解密函数，可以看到是不同的函数地址。在图的中间，是我的gdb调试过程，将左侧的三处函数地址分别存放在$func,$func3和$func4变量中，并类型转换成函数指针放在$f, $f3, $f4变量中。将左侧图的加密字符串地址计算出分别存放在$27, $f3_arg, $f4_arg中。分别执行$f($27), $f3($f3_arg), $f4($f4_arg)，得到结果"libc.so", "_exit", "exit"。 这里还有另外两处的解密函数和加密字符串，$f1($50)和$f2($57)，它的结果是"libdl.so"和"pwrite"。当我将使用$f2去解密$50时，解密失败了。解密的函数还有许多，就是开篇时说的未知数N。

下面我懒得去逆向分析，直接将其中的一个解密函数dump出来，并且在正在调试libbaiduprotect.so的移植python上映射一个执行区，然后直接去调用。

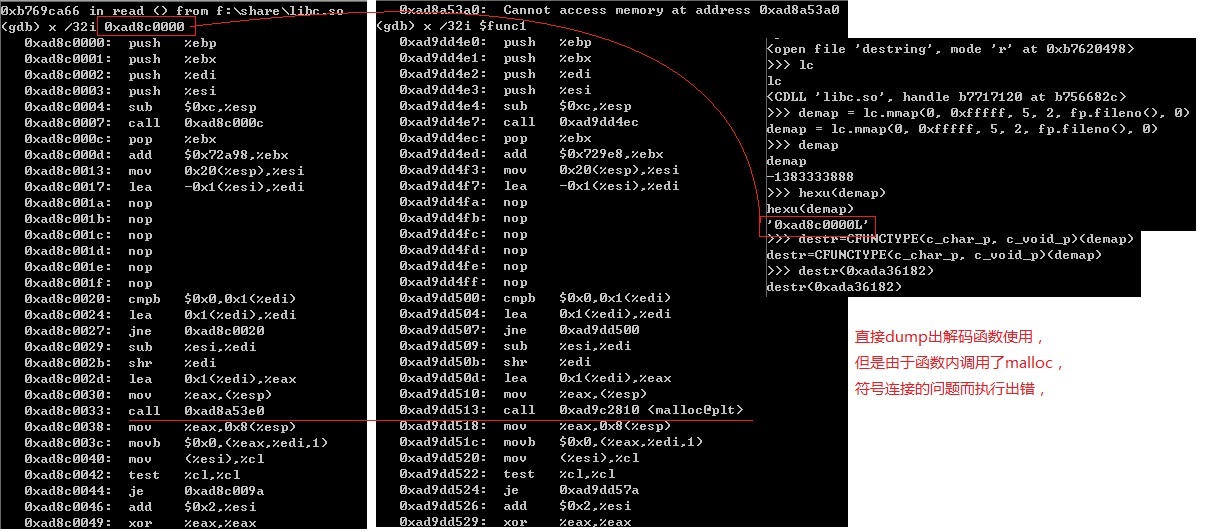
由于解密函数内部调用了其它库的函数，符号连接没有做处理，访问出错，只要处理好符号连接就可以直接使用里面的解密函数？

还不行，每个解密函数还单独对应一组密钥窗口。

下面摘取其中一个解密函数进行逆向分析：

   0xad9dd430:    push   %ebp
   0xad9dd431:    push   %ebx
   0xad9dd432:    push   %edi
   0xad9dd433:    push   %esi
   0xad9dd434:    sub    $0xc,%esp        　　    ; 距离上一栈帧 0x1c
   0xad9dd437:    call   0xad9dd43c
   0xad9dd43c:    pop    %ebx            　　     ; %ebx = %eip 　　// 使用eip定位全局变量
   0xad9dd43d:    add    $0x72a98,%ebx           ; %ebx = 0xad9dd43c + 0x72a98
   0xad9dd443:    mov    0x20(%esp),%esi         ; %esi = arg_1 　　// 函数输入加密编码字符串
   0xad9dd447:    lea    -0x1(%esi),%edi         ; while(*(((char*)%edi++)+1) != 0);　　// 计算加密字节流长度
   0xad9dd450:    cmpb   $0x0,0x1(%edi)
   0xad9dd454:    lea    0x1(%edi),%edi
   0xad9dd457:    jne    0xad9dd450
   0xad9dd459:    sub    %esi,%edi        　　　　; %edi = (int) ((char*)%edi - (char*)%esi)
   0xad9dd45b:    shr    %edi            　　　　 ; %edi >>= 1
   0xad9dd45d:    lea    0x1(%edi),%eax        　; %eax = %edi + 1      // 解码字符串长度
   0xad9dd460:    mov    %eax,(%esp)
   0xad9dd463:    call   0xad9c2810 <malloc@plt> ; char* var_8 = (char*) malloc(%eax)
   0xad9dd468:    mov    %eax,0x8(%esp)
   0xad9dd46c:    movb   $0x0,(%eax,%edi,)    　; var_8 [ %edi ] = 0
   0xad9dd470:    mov    (%esi),%cl        　　　 ; %cl = *(char*)%esi
   0xad9dd472:    test   %cl,%cl            　　　; if (%cl != 0) {
   0xad9dd474:    je     0xad9dd4ca
   0xad9dd476:    add    $0x2,%esi               ;  %esi += 2
   0xad9dd479:    xor    %eax,%eax               ;  %eax = 0        // 常量0
   0xad9dd47b:    xor    %edi,%edi               ;  %edi = 0        // 用作计数器，[0, 7]，指定解码的key
   0xad9dd47d:    mov    0x8(%esp),%ebp          ;  %ebp = var_8        // 用作遍历 var_8 的指针
   0xad9dd490:    movsbl %cl,%edx                ;  %edx = (int) %cl    // 下一轮循环入口，也就是解码下一对加密字符
   0xad9dd493:    shl    $0x4,%cl                ;  %cl <<= 4
   0xad9dd496:    cmp    $0x3a,%edx              ;  if (%edx >= 0x3a) {
   0xad9dd499:    jl     0xad9dd49e
   0xad9dd49b:    add    $0x90,%cl               ;    %cl += 0x90
   0xad9dd49e:    movsbl -0x1(%esi),%edx         ;  }  %edx = (int) *(char*)(%esi - 1)    // 紧接配对的下一个加密字符
   0xad9dd4a2:    cmp    $0x3a,%edx              ;
   0xad9dd4a5:    mov    $0xd0,%ch               ;  %ch = 0xd0
   0xad9dd4a7:    jl     0xad9dd4ab              ;  if (%edx >= 0x3a) {
   0xad9dd4a9:    mov    $0xc9,%ch               ;     %ch = 0xc9
   0xad9dd4ab:    add    %dl,%cl                 ;  }   %cl += %dl
   0xad9dd4ad:    add    %ch,%cl                 ;  %cl += %ch                // 化简 %cl += %dl + (%edi >= 0x3a) ? 0xc9 : 0xd0
   0xad9dd4af:    cmp    $0x8,%edi               ;
   0xad9dd4b2:    cmove  %eax,%edi               ;  %edi = (0x8 == %edi) ? %eax : %edi    // %eax 这时为0
   0xad9dd4b5:    xor    -0x138df(%ebx,%edi,),%cl;  %cl ^= 一个全局变量            // 一组解码的key，每个字符的解码相应一个key，滚动使用一个key窗口，防破解
   0xad9dd4bc:    mov    %cl,0x0(%ebp)           ;  *(char*) %ebp = %cl
   0xad9dd4bf:    inc    %ebp                    ;  %ebp++
   0xad9dd4c0:    inc    %edi                    ;  %edi++
   0xad9dd4c1:    mov    (%esi),%cl              ;  %cl = *(char*) %esi     // 下一对加密字符的第一个字符
   0xad9dd4c3:    add    $0x2,%esi               ;  %esi += 2
   0xad9dd4c6:    test   %cl,%cl                 ;  if (%cl != 0)
   0xad9dd4c8:    jne    0xad9dd490              ;     goto 0xad9dd490    // 循环
   0xad9dd4ca:    mov    0x8(%esp),%eax          ; } %eax = var_8
   0xad9dd4ce:    add    $0xc,%esp               ;
   0xad9dd4d1:    pop    %esi
   0xad9dd4d2:    pop    %edi
   0xad9dd4d3:    pop    %ebx
   0xad9dd4d4:    pop    %ebp
   0xad9dd4d5:    ret                            ; return (char*) %eax

上面的反汇编逻辑并不难，完全不借助工具分析也可以手工逆向。

工作原理：

1.字符串每个字符被加密成一个双字节，并以0结束。一个n长度的字符串，它的加密字节串长度为2n，然后以0作为额外结束符。

2.解密一个字符，必须参照一双加密字节，解密出一个字节。然后还要将这个得出的字节，使用密钥字节进行异或才能最后还原出正确的字符。

3.使用一组总数为8的密钥窗口，对解密过程进行滚动使用。每个字符的解密都对应其中的一个密钥。

从上面的工作原理可以有这样的解密失配的结果：

1.当一个偶地址开始的加密字节串，如果在其中中间的某个奇地址开始进行解密的话，解密过程中，由双字节得到单字节都将是错误的，因这过程的双字节失配了。反之亦然。

2.即使双字节没有失配，如果加密字节串的起始地址没有与密钥窗口对上，同样字符的解密失败。比如说我们在加密字节串起始地址偏移了2*n个单位进行解密，则会解密错误。

3.当每个解密函数使用独立的密钥窗口时，加密字节串就必须使用相配的密钥窗口的解密函数才能将字符串解密出来。

4.当你不清楚每个加密字节串的起始地址，而暴力破解时，那不是M个字符串 x (N个解密函数 - 1) 次失配了，而 .rodata长度 x (N个解密函数）- M个字符串 次失配。尽管我们可以假定每个加密字节串的起始位于前一个加密字节串的结束符之后，来减少暴力次数，但也只是假定。