POJ 3463 最（次）短路条数

Sightseeing

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 9497		Accepted: 3340

Description

Tour operator Your Personal Holiday organises guided bus trips across the Benelux. Every day the bus moves from one city S to another city F. On this way, the tourists in the bus can see the sights alongside the route travelled. Moreover, the bus makes a number of stops (zero or more) at some beautiful cities, where the tourists get out to see the local sights.

Different groups of tourists may have different preferences for the sights they want to see, and thus for the route to be taken from S to F. Therefore, Your Personal Holiday wants to offer its clients a choice from many different routes. As hotels have been booked in advance, the starting city S and the final city F, though, are fixed. Two routes from S to F are considered different if there is at least one road from a city A to a city B which is part of one route, but not of the other route.

There is a restriction on the routes that the tourists may choose from. To leave enough time for the sightseeing at the stops (and to avoid using too much fuel), the bus has to take a short route from S to F. It has to be either a route with minimal distance, or a route which is one distance unit longer than the minimal distance. Indeed, by allowing routes that are one distance unit longer, the tourists may have more choice than by restricting them to exactly the minimal routes. This enhances the impression of a personal holiday.

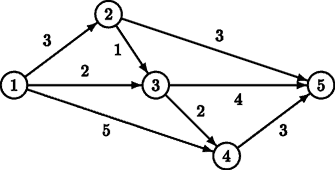
For example, for the above road map, there are two minimal routes from S = 1 to F = 5: 1 → 2 → 5 and 1 → 3 → 5, both of length 6. There is one route that is one distance unit longer: 1 → 3 → 4 → 5, of length 7.

Now, given a (partial) road map of the Benelux and two cities S and F, tour operator Your Personal Holiday likes to know how many different routes it can offer to its clients, under the above restriction on the route length.

Input

The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:

• One line with two integers N and M, separated by a single space, with 2 ≤ N ≤ 1,000 and 1 ≤ M ≤ 10, 000: the number of cities and the number of roads in the road map.

• M lines, each with three integers A, B and L, separated by single spaces, with 1 ≤ A, B ≤ N, A ≠ B and 1 ≤ L ≤ 1,000, describing a road from city A to city B with length L.

  The roads are unidirectional. Hence, if there is a road from A to B, then there is not necessarily also a road from B to A. There may be different roads from a city A to a city B.

• One line with two integers S and F, separated by a single space, with 1 ≤ S, F ≤ N and S ≠ F: the starting city and the final city of the route.

  There will be at least one route from S to F.

Output

For every test case in the input file, the output should contain a single number, on a single line: the number of routes of minimal length or one distance unit longer. Test cases are such, that this number is at most 10⁹ = 1,000,000,000.

Sample Input

2
5 8
1 2 3
1 3 2
1 4 5
2 3 1
2 5 3
3 4 2
3 5 4
4 5 3
1 5
5 6
2 3 1
3 2 1
3 1 10
4 5 2
5 2 7
5 2 7
4 1

Sample Output

3
2

Hint

The first test case above corresponds to the picture in the problem description.

题意：旅行团每天固定的从S地出发到达T地，为了省油要求尽量走最短路径或比最短路径长1单位距离的路径，求满足条件的路径条数

算法：最短路和次短路。Dijkstra算法。采用邻接表建图。

dis[x][2]:dis[x][0]表示起点到x的最短路、dis[x][1]表示起点到x的次短路；

arr[x][2]:arr[x][0]表示起点到x的最短路条数、arr[x][1]表示起点到x的次短路的条数；

vis[x][2]对应于x和0、1功能为记录该点是否被访问！

那么如何更新最小和次小路呢？显然我们容易想到下面的方法：

1.if(x<最小)更新最小，次小；
      2.else if(x==最小)更新方法数；
      3.else if(x<次小)更新次小；
      4.else if(x==次小)更新方法数；

最后说说dijkstra的循环部分、这也是本题的关键。为什么我们要循环2*nnum-1次？显然这道题中我们每一条边都需要考虑、这不是在求最短的一条，说白了是让你求出所有的可能组合，那么我们势必对每一种情况都需要遍历一次，虽然中间有重复。最短路里已知[start][0]已被标记为访问过，那么就只有nnum-1次遍历了，而次短路我们则需要遍历nnum次，这样两者加起来就为2*nnum-1次。这与我们平时使用优先队列+heap是一样的。只是更加细化了而已。

代码：

 //#include<bits/stdc++.h>
 //#include<regex>
 #include <vector>
 #include <cstdio>
 #include "cstring"
 #include <algorithm>
 #define db double
 #define ll long long
 #define vec vector<ll>
 #define Mt  vector<vec>
 #define ci(x) scanf("%d",&x)
 #define cd(x) scanf("%lf",&x)
 #define cl(x) scanf("%lld",&x)
 #define pi(x) printf("%d\n",x)
 #define pd(x) printf("%f\n",x)
 #define pl(x) printf("%lld\n",x)
 #define MP make_pair
 #define PB push_back
 #define fr(i,a,b) for(int i=a;i<=b;i++)
 using namespace std;
 const int N=1e6+;
 const int mod=1e9+;
 const int MOD=mod-;
 const db  eps=1e-;
 //const db  pi = acos(-1.0);
 const int inf = 0x3f3f3f3f;
 const ll  INF = 0x3f3f3f3f3f3f3f3f;
 int h[N],d[N][],c[N][];
 bool vis[N][];
 struct P
 {
     int v,w,nx;
     P(int x,int y,int z):v(x),w(y),nx(z){};
     P(){};
 };
 vector<P> e;
 int cnt,n,m,t;
 void add(int x,int y,int z)
 {

     e.push_back(P(y,z,h[x]));
     h[x]=cnt++;
 }
 void dij(int s,int g)
 {
     memset(vis,, sizeof(vis));
     memset(c,, sizeof(c));
     for(int i=;i<=n;i++){
         d[i][]=inf;
         d[i][]=inf;
     }
     int k,ok;
     d[s][]=,c[s][]=;

     for(int ii=;ii<*n;ii++)
     {
         int ans=inf;
         for(int i=;i<=n;i++){
             if(!vis[i][]&&d[i][]<ans){//取最近的点
                 k=i;
                 ok=;
                 ans=d[i][];
             }
             else if(!vis[i][]&&d[i][]<ans){
                 k=i;
                 ok=;
                 ans=d[i][];
             }
         }
         if(ans==inf) break;
         vis[k][ok]=;
         for(int j=h[k];j!=-;j=e[j].nx){
             int v=e[j].v,w=e[j].w;
             if(d[v][]>ans+w){//更新最短路
                 d[v][]=d[v][];
                 c[v][]=c[v][];
                 d[v][]=ans+w;
                 c[v][]=c[k][ok];
             }
             else if(d[v][]==ans+w){//更新最短路条数
                 c[v][]+=c[k][ok];
             }
             else if(d[v][]>ans+w)//更新次短路
                 d[v][]=ans+w,c[v][]=c[k][ok];
             else if(d[v][]==ans+w)//次短路条数
                 c[v][]+=c[k][ok];
         }
     }
     if(d[g][]==d[g][]+)
         c[g][]+=c[g][];

     pi(c[g][]);

 }
 int main()
 {
     ci(t);
     while(t--)
     {
         ci(n),ci(m);
         e.clear();
         cnt=;
         memset(h,-, sizeof(h));
         for(int i=;i<m;i++){
             int x,y,z;
             ci(x),ci(y),ci(z);
             add(x,y,z);
         }
         int s,g;
         ci(s),ci(g);
         dij(s,g);
     }
     return ;

 }