一、二元分类的线性模型

线性分类、线性回归、逻辑回归

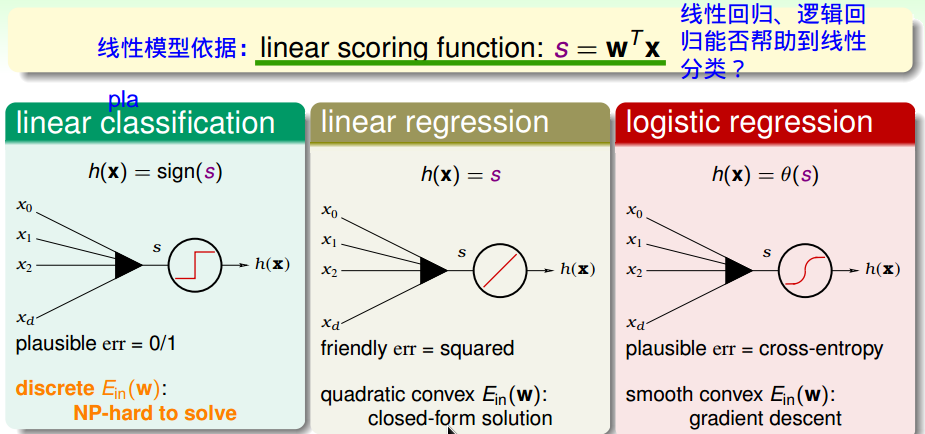
可视化这三个线性模型的代价函数

SQR、SCE的值都是大于等于0/1的

理论分析上界

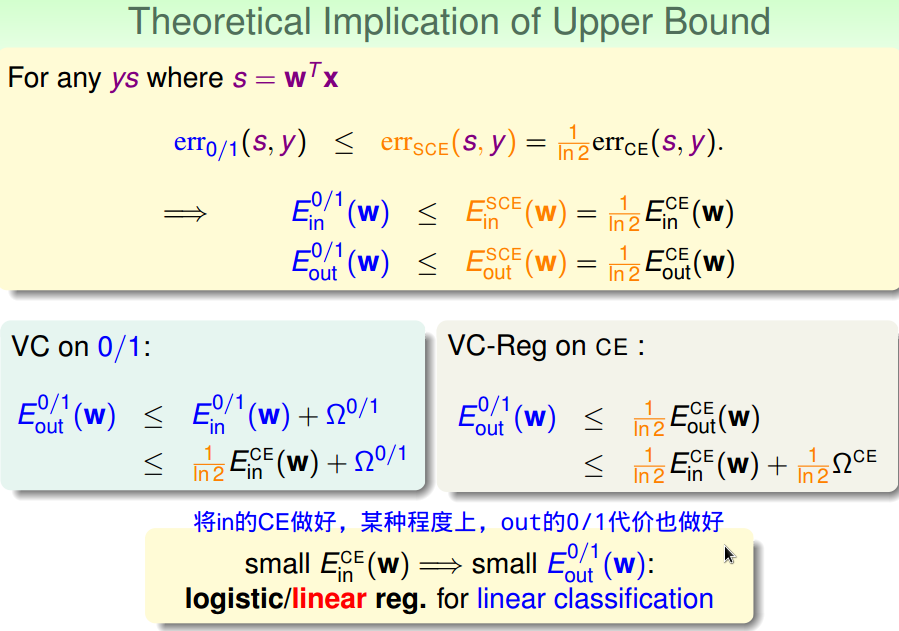
将回归应用于分类

线性回归后的参数值常用于pla/pa/logistic regression的参数初始化

二、随机梯度下降

两种迭代优化模式

利用全部样本---》利用随机的单个样本，

梯度下降---》随机梯度下降

SGD与PLA的相似性

当迭代次数足够多时，停止

步长常取0.1

三、使用逻辑回归的多分类问题

是非题---》选择题

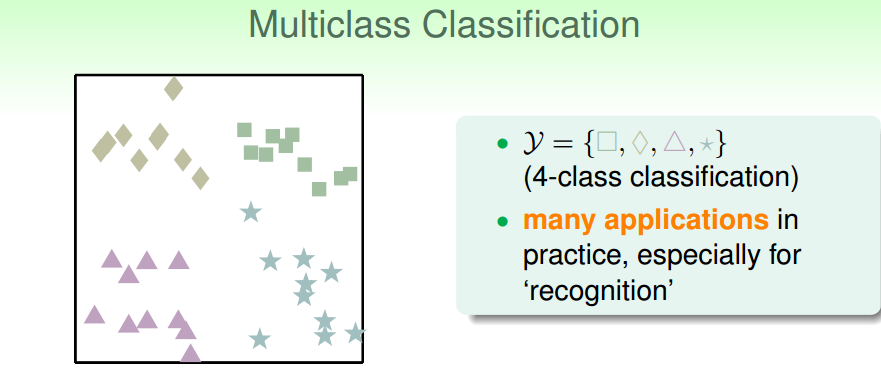
每次识别一类A，将其他类都视作非A类

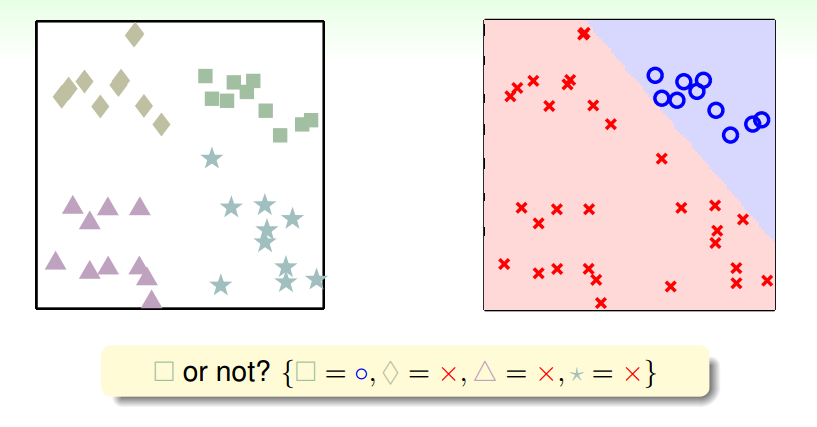
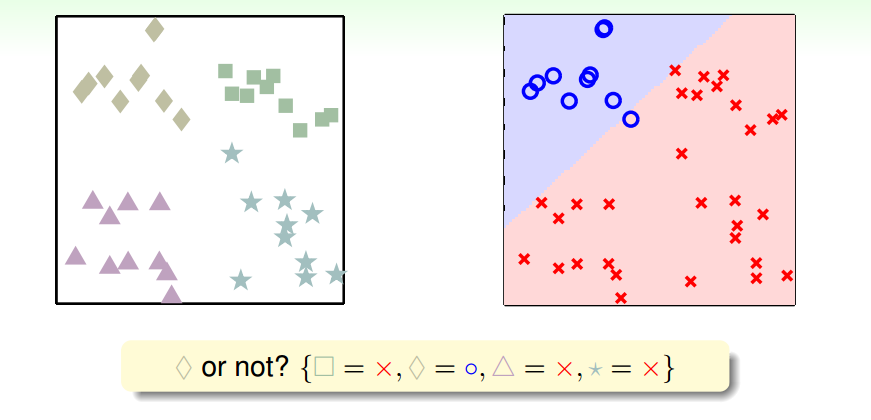
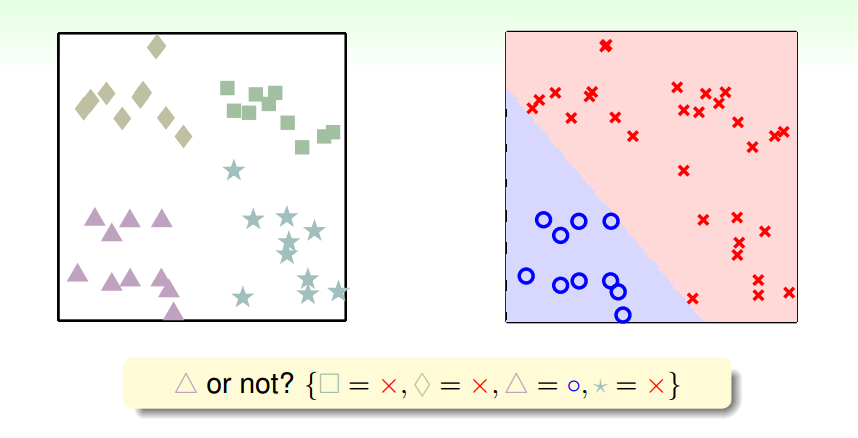
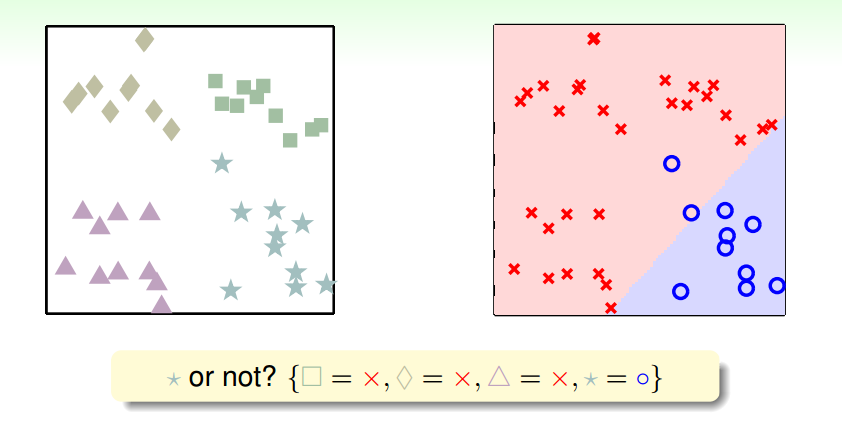
结果出现问题

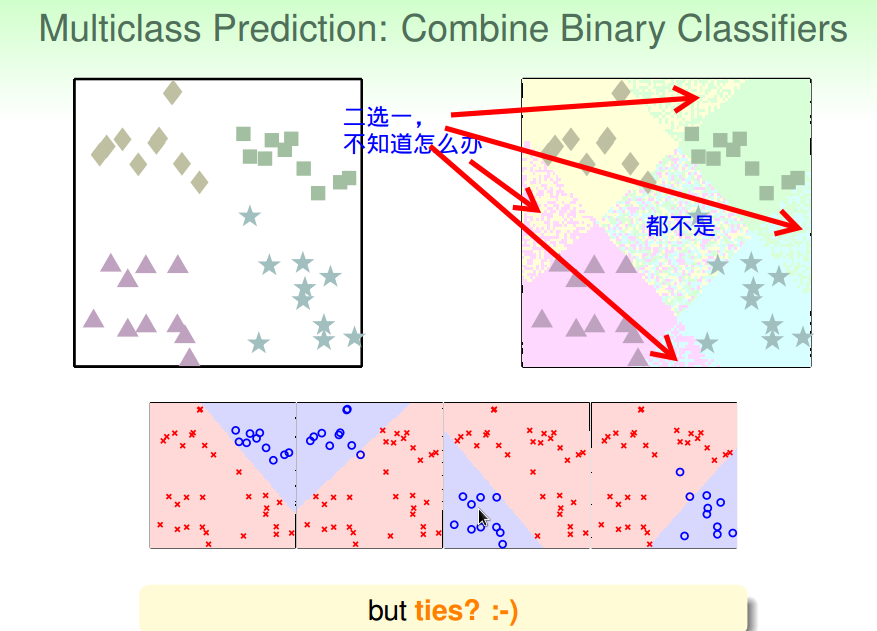
将是不是A类变为是A类的可能性：软分类

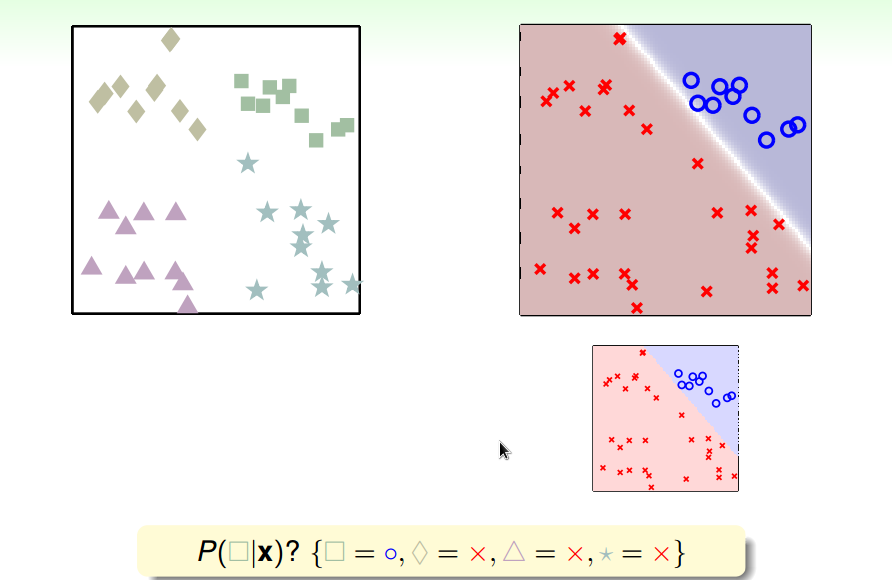
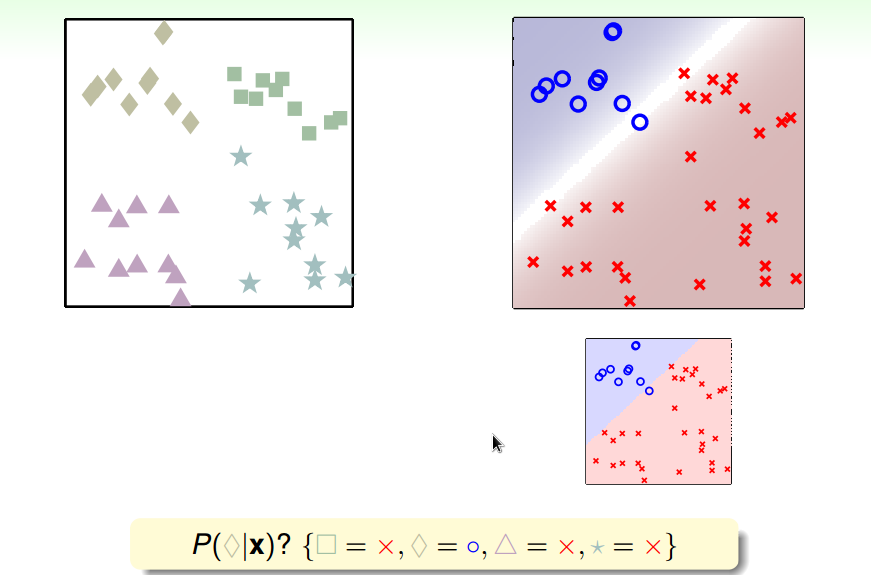
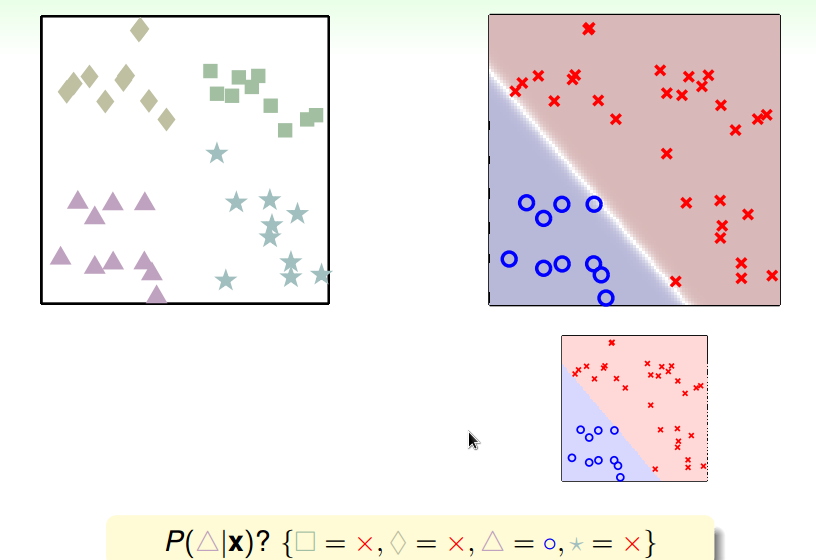
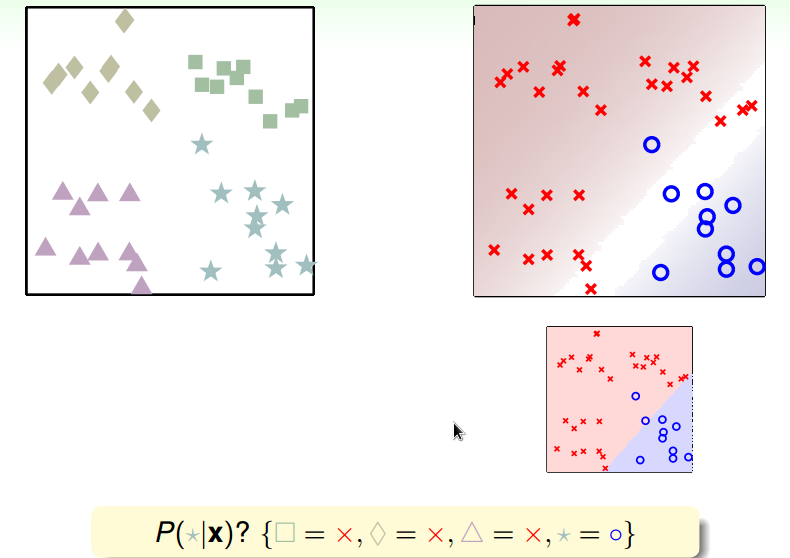
分别计算属于某类的概率，取概率值最大的类为最后的分类结果

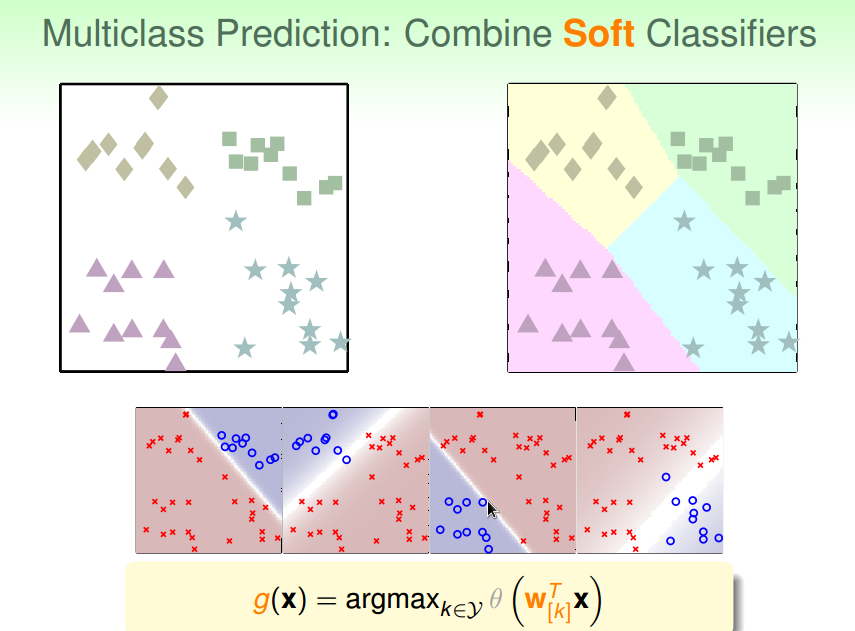
OVA总结

注意每次计算一类概率时都得利用全部样本

四、使用二元分类的多分类问题

OVA经常不平衡，即属于某类的样本过多时，分类结果往往倾向于该类

为更加平衡，使用OVO

OVA保留一类，其他为非该类，每次利用全部样本；

OVO保留两类，每次只利用属于这两类的样本

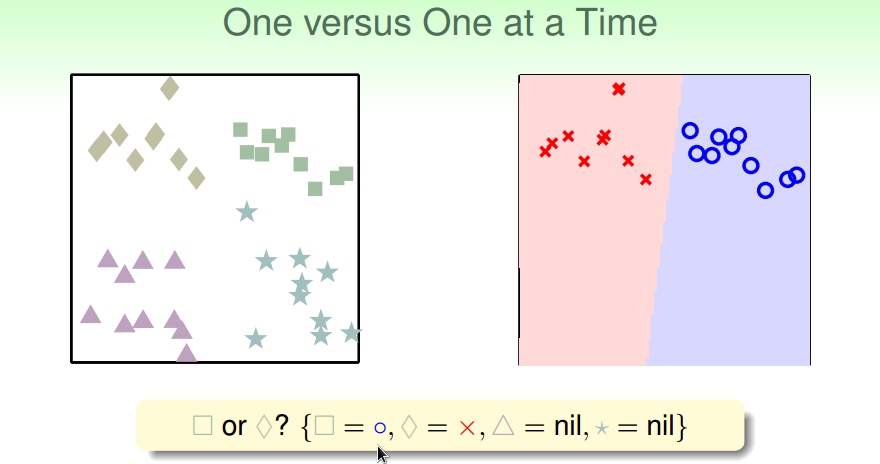
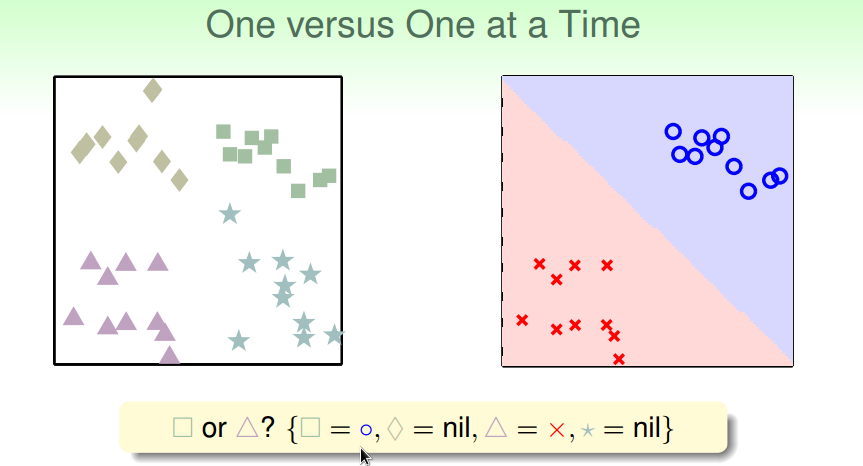
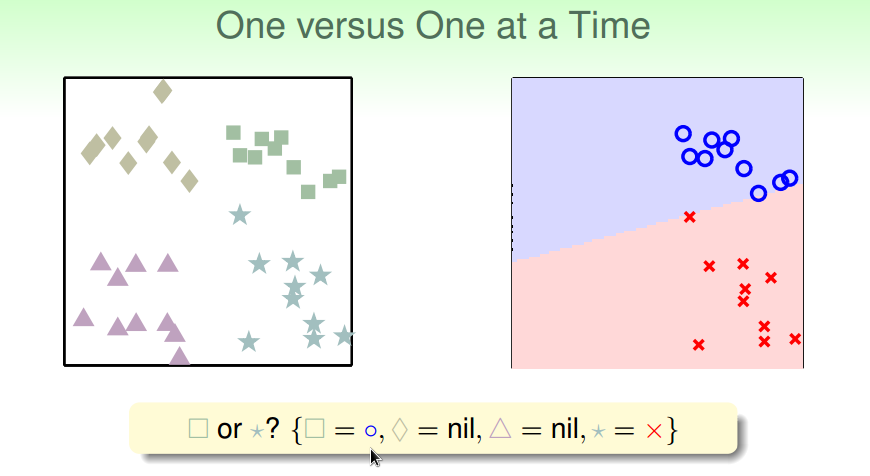
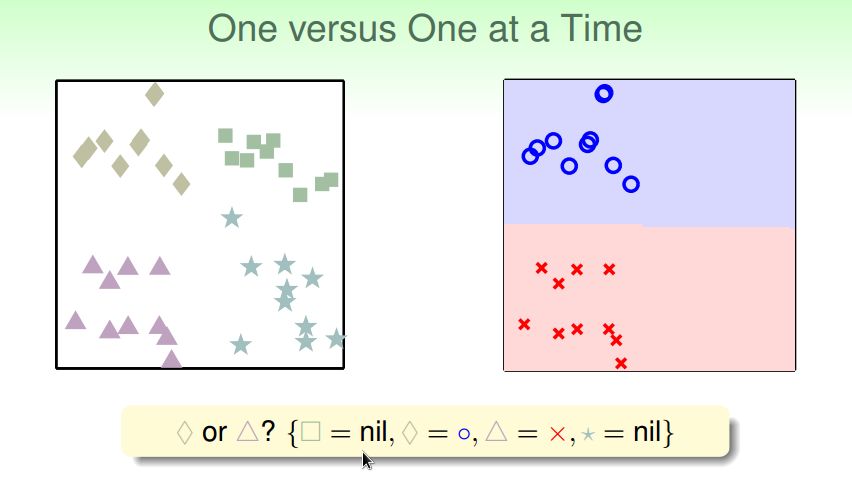
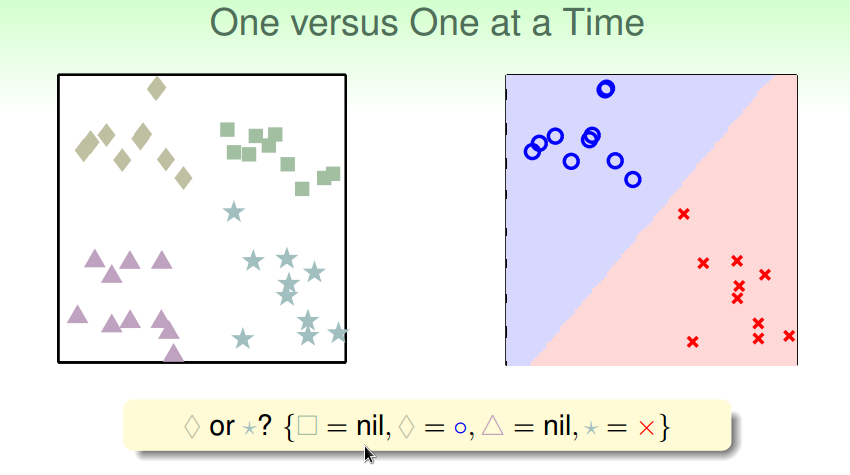
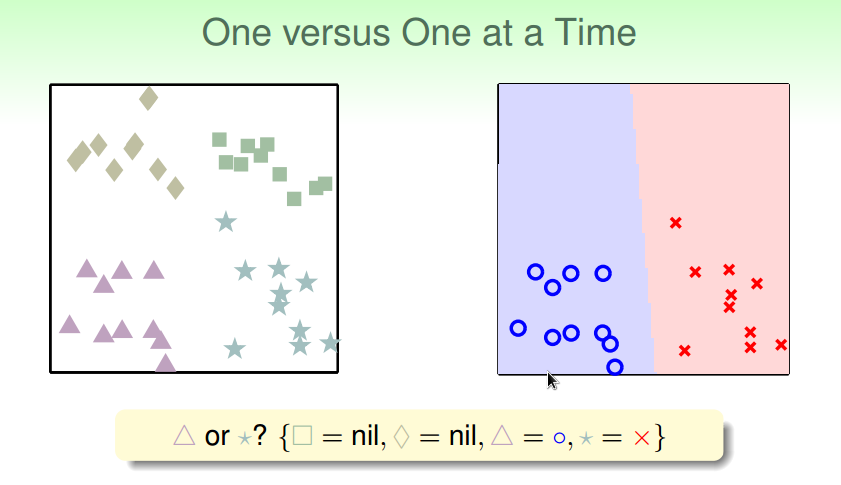
通过投票得出最终分类结果

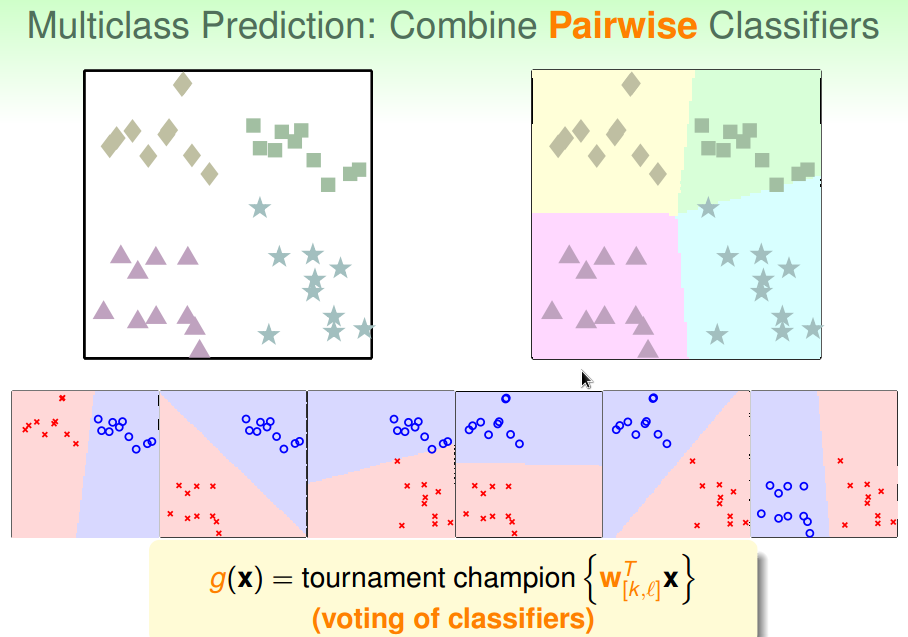
OVO总结

OVA vs OVO

11 Linear Models for Classification的更多相关文章

  1. 机器学习基石笔记：11 Linear Models for Classification

    一.二元分类的线性模型 线性分类.线性回归.逻辑回归: 可视化这三个线性模型的代价函数, SQR.SCE的值都是大于等于0/1的. 理论分析上界: 将回归应用于分类: 线性回归后的参数值常用于pla/ ...

  2. 机器学习基石笔记：11 Linear Models for Classification、LC vs LinReg vs LogReg、OVA、OVO

    原文地址:https://www.jianshu.com/p/6f86290e70f9 一.二元分类的线性模型 线性回归后的参数值常用于PLA/PA/Logistic Regression的参数初始化 ...

  3. PRML读书会第四章 Linear Models for Classification(贝叶斯marginalization、Fisher线性判别、感知机、概率生成和判别模型、逻辑回归)

    主讲人 planktonli planktonli(1027753147) 19:52:28 现在我们就开始讲第四章,第四章的内容是关于 线性分类模型,主要内容有四点:1) Fisher准则的分类,以 ...

  4. Coursera台大机器学习课程笔记10 -- Linear Models for Classification

    这一节讲线性模型,先将几种线性模型进行了对比,通过转换误差函数来将linear regression 和logistic regression 用于分类. 比较重要的是这种图,它解释了为何可以用Lin ...

  5. 《机器学习基石》---Linear Models for Classification

    1 用回归来做分类 到目前为止,我们学习了线性分类,线性回归,逻辑回归这三种模型.以下是它们的pointwise损失函数对比(为了更容易对比,都把它们写作s和y的函数,s是wTx,表示线性打分的分数) ...

  6. Regression：Generalized Linear Models

    作者:桂. 时间:2017-05-22  15:28:43 链接:http://www.cnblogs.com/xingshansi/p/6890048.html 前言 本文主要是线性回归模型,包括: ...

  7. Generalized Linear Models

    作者:桂. 时间:2017-05-22  15:28:43 链接:http://www.cnblogs.com/xingshansi/p/6890048.html 前言 主要记录python工具包:s ...

  8. [Scikit-learn] 1.5 Generalized Linear Models - SGD for Classification

    NB: 因为softmax,NN看上去是分类,其实是拟合(回归),拟合最大似然. 多分类参见:[Scikit-learn] 1.1 Generalized Linear Models - Logist ...

  9. ON THE EVOLUTION OF MACHINE LEARNING: FROM LINEAR MODELS TO NEURAL NETWORKS

    ON THE EVOLUTION OF MACHINE LEARNING: FROM LINEAR MODELS TO NEURAL NETWORKS We recently interviewed ...

随机推荐

  1. css中滚动条样式的设置

    参数说明: 1.overflow-y : 设置当对象的内容超过其指定高度时如何管理内容:overflow-x : 设置当对象的内容超过其指定宽度时如何管理内容. 参数: visible:扩大面积以显示 ...

  2. Ajax新玩法fetch API

    目前 Web 异步应用都是基于 XMLHttpRequest/ActiveXObject (IE)实现的, 这些对象不是专门为资源获取而设计的,因而它们的 API 非常复杂,同时还需要开发者处理兼容性 ...

  3. C#使用Xamarin开发可移植移动应用进阶篇(9.混淆代码,防止反编译)

    前言 系列目录 C#使用Xamarin开发可移植移动应用目录 源码地址:https://github.com/l2999019/DemoApp 可以Star一下,随意 - - 说点什么.. 今天讲讲如 ...

  4. Spring Boot之Hello World

    Spring Boot简介 Spring Boot是由Pivotal团队提供的全新框架,其设计目的是用来简化新Spring应用的初始搭建以及开发过程.该框架使用了特定的方式来进行配置,从而使开发人员不 ...

  5. wpf创建用户控件（计时器控件）

    在vs中新增用户控件 前台xaml如下代码: <UserControl x:Class="Zh.SelfServiceEquipment.UI.ZhControls.CountDown ...

  6. jquery获取json对象中的key小技巧

    jquery获取json对象中的key小技巧 比如有一个json var json = {"name" : "Tom", "age" : 1 ...

  7. 我的天哪，现在的移动VIN码识别已经这么。。

    VIN码是英文(Vehicle Identification Number)的缩写,译为车辆识别代码,又称车辆识别码,车辆识别代码,车辆识别号,车辆识别代号,VIN码是表明车辆身份的代码.VIN码由1 ...

  8. ★RFC标准库_目录链接

    RFC(Request For Comments)是一个国际标准化的数据库,记录了从计算机到互联网的海量标准协议.它是一个免费公开的IT标准文件分享平台,其内容也在不断增长,与时俱进.它与ISO等组织 ...

  9. 团队作业9——展示博客（Bata版本）

    1.团队成员介绍及项目地址 团队的源码仓库地址:https://coding.net/u/app24dian/p/app24dian/git 陈麟凤:(http://www.cnblogs.com/c ...

  10. 201521123066 《Java程序设计》第四周学习总结

    1. 本周学习总结 1.1 尝试使用思维导图总结有关继承的知识点. 1.2 使用常规方法总结其他上课内容. 1.多态性: (1)概念:相同的方法名,不同的实现方法 (2)instanceof运算符:判 ...