【LeetCode题解】排序

1. 排序

排序（sort）是一种常见的算法，把数据根据特定的顺序进行排列。经典的排序算法如下：

• 冒泡排序（bubble sort）
• 插入排序（insertion sort）
• 选择排序（selection sort）
• 快速排序（quick sort）
• 堆排序（heap sort）
• 归并排序（merge sort）

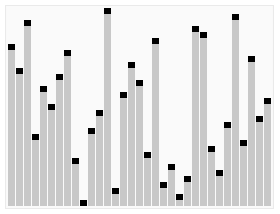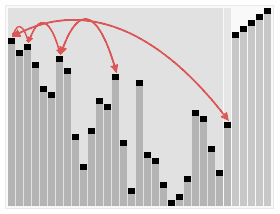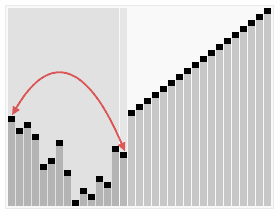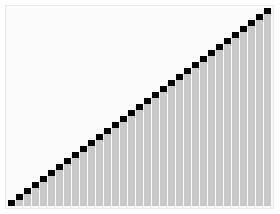
冒泡排序依次比较相邻的两个元素，若逆序则交换；如此走访数列重复n次，即不再发生交换，排序完成。（以下图片均来自于Wikipedia）

但是，冒泡排序存在着许多无意义的交换，比如：对于基本有序的数组（最好情况），冒泡排序仍旧有\(O(n^2)\)次交换。我们可以标记需要交换的可能，从而降低交换次数到\(O(n)\)：

void bubble_sort(int a[], int n) {
  int i, bound;
  int exchange = n - 1;       // 初始化
  while (exchange) {
    bound = exchange; // 记录上一次的交换位置
    exchange = 0;     // 假定这一次没发生交换
    for (i = 0; i < bound; i++)
      if (a[i] > a[i + 1]) {
        swap(&a[i], &a[i + 1]);
        exchange = i;
      }
  }
}

插入排序能很好地避免部分无意义的交换，其核心思想：从前往后扫描序列，已扫描的元素构成一个已排序的有序序列，当前扫描的元素作为待插入元素，从有序序列中找到其适合的位置进行插入。

选择排序是一种直观的排序算法，其基本思想：从前往后走访待排序序列，找出最小的元素置于待排序序列的首端；如此往复，直到待排序序列只包含一个元素。

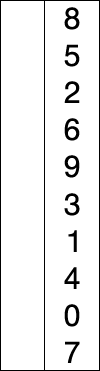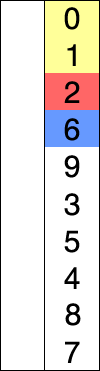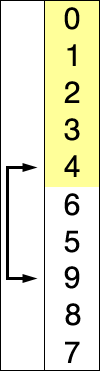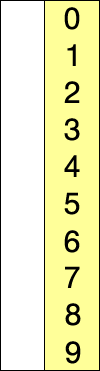
快速排序是由Hoare提出，采用了分治（divide and conquer）策略：选取一个基准pivot，将序列划分为两个子序列，比pivot小的元素归为左子序列，比pivot大（或等于）归于右子序列；如此递归地划分子序列直到无需划分（即整体有序）。此划分操作也被称为partition；下图给出以元素5为pivot的partition操作：

堆排序是指利用大顶堆（max heap）进行排序的算法，基本思想：依次删除堆顶元素（待排序序列的最大值），将其置于待排序序列的末端；如此往复，直至堆为空。

归并排序也是采用分治策略：将相邻两个有序的子序列进行归并（merge）操作，如此往复，直到归并成一个完整序列（排序完成）。初始时，子序列对应于每一个元素。

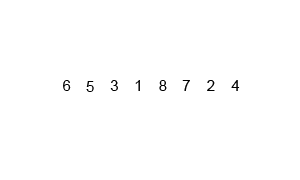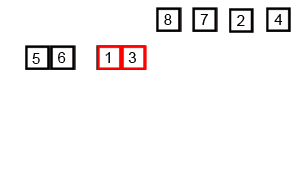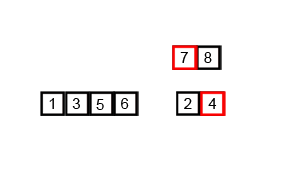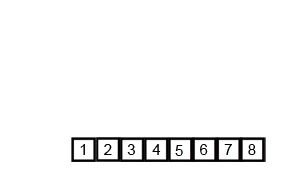
稳定性是衡量排序算法是否改变相等键值的次序的指标。典型地，比如快排因pivot的选取可能会改变相等键值的次序。各种排序算法的比较如下：

排序算法	时间复杂度	空间复杂度	稳定性
冒泡排序	\(O(n^2)\)	\(T(1)\)	稳定
插入排序	\(O(n^2)\)	\(T(1)\)	稳定
选择排序	\(O(n^2)\)	\(T(1)\)	不稳定
快速排序	\(O(n \log n)\)	\(T(1)\)	不稳定
堆排序	\(O(n \log n)\)	\(T(1)\)	不稳定
归并排序	\(O(n \log n)\)	\(T(\log n)\)	稳定

2. 题解

LeetCode题目	归类
75. Sort Colors
349. Intersection of Two Arrays	插入
148. Sort List	归并
242. Valid Anagram
56. Merge Intervals
57. Insert Interval
274. H-Index
275. H-Index II
179. Largest Number
349. Intersection of Two Arrays
350. Intersection of Two Arrays II

75. Sort Colors

数字0、1、2排序，采取类似选择排序的思路，数字0放在首端，数字2放在尾端。

public void sortColors(int[] nums) {
  int low = 0, high = nums.length - 1;
  for (int k = 0; k <= high; k++) {
    if (nums[k] == 0)
      swap(nums, k, low++);
    else if (nums[k] == 2)
      swap(nums, k--, high--);
  }
}

private void swap(int[] A, int a, int b) {
  int temp = A[a];
  A[a] = A[b];
  A[b] = temp;
}

349. Intersection of Two Arrays

链表的插入排序。

public ListNode insertionSortList(ListNode head) {
  ListNode nHead = new ListNode(0), p = head, pNext, np, nPre;
  while (p != null) {
    // find the suitable position to insert
    for (np = nHead.next, nPre = nHead; np != null && np.val < p.val; ) {
      np = np.next;
      nPre = nPre.next;
    }
    nPre.next = p;
    pNext = p.next;
    p.next = np;
    p = pNext;
  }
  return nHead.next;
}

148. Sort List

排序链表，要求时间复杂度\(O(n \log n)\)、空间复杂度\(T(1)\)，所以使用归并排序。其中，合并两个有序链表复用了问题21. Merge Two Sorted Lists的代码。

public ListNode sortList(ListNode head) {
  if (head == null || head.next == null) return head;
  ListNode pre = head, slow = head, fast = head;
  // cut the list into two halves
  while (fast != null && fast.next != null) {
    pre = slow;
    slow = slow.next;
    fast = fast.next.next;
  }
  pre.next = null;
  // sort the two halves
  ListNode l1 = sortList(head);
  ListNode l2 = sortList(slow);
  // merge the two sorted halves
  return mergeTwoLists(l1, l2);
}

242. Valid Anagram

判断两个字符串是否同构（变位词）。将values数组排序后，判断是否相等。

public boolean isAnagram(String s, String t) {
  char[] sValues = s.toCharArray();
  char[] tValues = t.toCharArray();
  Arrays.sort(sValues);
  Arrays.sort(tValues);
  return Arrays.equals(sValues, tValues);
}

56. Merge Intervals

合并重复的区间段。思路：排序区间，然后根据条件进行合并。

public List<Interval> merge(List<Interval> intervals) {
  if (intervals.size() <= 1) return intervals;
  intervals.sort((i1, i2) -> {
    if (i1.start == i2.start) return i1.end - i2.end;
    return i1.start - i2.start;
  });
  List<Interval> result = new ArrayList<>();
  for (int i = 0; i < intervals.size(); ) {
    int j, margin = intervals.get(i).end;
    for (j = i + 1; j < intervals.size(); j++) {
      if (intervals.get(j).start > margin)
        break;
      margin = Math.max(margin, intervals.get(j).end);
    }
    result.add(new Interval(intervals.get(i).start, margin));
    i = j;
  }
  return result;
}

57. Insert Interval

将一个区间插入到有序区间列表中，若有重复区间则需要做合并。

public List<Interval> insert(List<Interval> intervals, Interval newInterval) {
  LinkedList<Interval> result = new LinkedList<>();
  if (intervals == null || intervals.isEmpty()) {
    result.add(newInterval);
    return result;
  }
  int len = intervals.size(), start, end, j;
  Interval interval;
  boolean hasAdded = false;
  for (int i = 0; i < len; ) {
    interval = intervals.get(i);
    if (interval.end < newInterval.start) { // newInterval is right-outside
      result.add(interval);
      i++;
    } else if (interval.start > newInterval.end) { // newInterval is left-outside
      if (!hasAdded) {
        result.add(newInterval);
        hasAdded = true;
      }
      result.add(interval);
      i++;
    } else {
      start = Math.min(interval.start, newInterval.start);
      end = Math.max(interval.end, newInterval.end);
      for (j = i + 1; j < len; j++) {
        interval = intervals.get(j);
        if (interval.start > end) break;
        end = Math.max(end, interval.end);
      }
      result.add(new Interval(start, end));
      hasAdded = true;
      i = j;
    }
  }
  if (!hasAdded) result.add(newInterval);
  return result;
}

274. H-Index

计算作者的h-index。思路：对引用次数数组排序，找出至少有h篇论文的引用次数>=h。

public int hIndex(int[] citations) {
  Arrays.sort(citations);
  int h = 0;
  for (int i = citations.length - 1; i >= 0; i--) {
    if (citations[i] < h + 1) break;
    h++;
  }
  return h;
}

275. H-Index II

与上类似，不同在于citations已排序，且是升序。

179. Largest Number

从一串数字中，找出能拼成的最大整数；相当于对整数字符串的排序。

public String largestNumber(int[] nums) {
  int len = nums.length;
  String[] strs = new String[len];
  for (int i = 0; i < len; i++) {
    strs[i] = String.valueOf(nums[i]);
  }
  Arrays.sort(strs, this::compareNum);
  // special case
  if (strs[0].charAt(0) == '0') return "0";
  StringBuilder builder = new StringBuilder();
  for (String str : strs) {
    builder.append(str);
  }
  return builder.toString();
}

// compare two number-strings
private int compareNum(String num1, String num2) {
  String cat1 = num1 + num2;
  String cat2 = num2 + num1;
  return cat2.compareTo(cat1);
}

349. Intersection of Two Arrays

求解两个数组的交集，并去重。思路：排序两个数组，然后做依次比较，用pre保存上一次添加元素（用于去重）。

public int[] intersection(int[] nums1, int[] nums2) {
  if (nums1 == null || nums2 == null) return null;
  Arrays.sort(nums1);
  Arrays.sort(nums2);
  int len1 = nums1.length, len2 = nums2.length, pre = 0;
  boolean hasAdded = false;
  ArrayList<Integer> common = new ArrayList<>();
  for (int i = 0, j = 0; i < len1 && j < len2; ) {
    if (nums1[i] < nums2[j])
      i++;
    else if (nums1[i] > nums2[j])
      j++;
    else {
      if (nums1[i] != pre || !hasAdded) {
        common.add(nums1[i]);
        pre = nums1[i];
        hasAdded = true;
      }
      i++;
      j++;
    }
  }
  int[] result = new int[common.size()];
  for (int i = 0; i < common.size(); i++) {
    result[i] = common.get(i);
  }
  return result;
}

350. Intersection of Two Arrays II

同上求交集，不需要做去重。