hdu_2604Queuing(快速幂矩阵)

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2604

Queuing

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4428    Accepted Submission(s): 1961

Problem Description

Queues and Priority Queues are data structures which are known to most computer scientists. The Queue occurs often in our daily life. There are many people lined up at the lunch time. 

  Now we define that ‘f’ is short for female and ‘m’ is short for male. If the queue’s length is L, then there are 2^L numbers of queues. For example, if L = 2, then they are ff, mm, fm, mf . If there exists a subqueue as fmf or fff, we call it O-queue else it is a E-queue.
Your task is to calculate the number of E-queues mod M with length L by writing a program.

 

Input

Input a length L (0 <= L <= 10 ⁶) and M.

 

Output

Output K mod M(1 <= M <= 30) where K is the number of E-queues with length L.

 

Sample Input

3 8
4 7
4 8

 

Sample Output

6
2
1

 

Author

WhereIsHeroFrom

 

Source

HDU 1st “Vegetable-Birds Cup” Programming Open Contest

 

 

注释：在思考一个递推公式的时候几乎都可以分类讨论一下然后写成一个矩阵乘的形式，然后递推得到结果。

 

题意：

用f(n)表示n个人满足条件的结果，那么如果最后一个人是m的话，那么前n-1个满足条件即可，就是f(n-1)； 
如果最后一个是f那么这个还无法推出结果，那么往前再考虑一位：那么后三位可能是：mmf, fmf, mff, fff，其中fff和fmf不满足题意所以我们不考虑，但是如果是 
mmf的话那么前n-3可以找满足条件的即：f(n-3)；如果是mff的话，再往前考虑一位的话只有mmff满足条件即：f(n-4) 
所以f(n)=f(n-1)+f(n-3)+f(n-4)，递推会跪，可用矩阵快速幂 
构造一个矩阵。

用f(n)表示n个人满足条件的结果，那么如果最后一个人是m的话，那么前n-1个满足条件即可，就是f(n-1)； 
如果最后一个是f那么这个还无法推出结果，那么往前再考虑一位：那么后三位可能是：mmf, fmf, mff, fff，其中fff和fmf不满足题意所以我们不考虑，但是如果是 
mmf的话那么前n-3可以找满足条件的即：f(n-3)；如果是mff的话，再往前考虑一位的话只有mmff满足条件即：f(n-4) 
所以f(n)=f(n-1)+f(n-3)+f(n-4)，递推会跪，可用矩阵快速幂 
构造一个矩阵：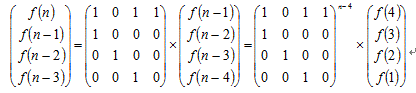 

 //快速幂矩阵
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 struct Mat
 {
     int mat[][];
 };
 int m;
 Mat operator *(Mat a, Mat b)
 {
     Mat c;
     memset(c.mat,,sizeof(c.mat));
     int i, j, k;
     //这儿的顺序按照
     for(i = ; i < ; i++)
         for(j = ; j < ; j++)
             for(k = ; k < ; k++)
                 c.mat[i][j] = (c.mat[i][j] + a.mat[i][k]*b.mat[k][j])%m;
     return c;
 }
 Mat multi(int n)//计算一个已知矩阵的n次方%m
 {
     Mat ans;
     for(int i = ; i < ; i++)
     {
         for(int j = ; j < ; j++)
         {
             if(i==j)
                 ans.mat[i][j] = ;
             else ans.mat[i][j] = ;
         }
 
     }
     Mat a;
     memset(a.mat,,sizeof(a.mat));
     a.mat[][] = a.mat[][] = a.mat[][] = a.mat[][] = a.mat[][] = a.mat[][] = ;
 
     while(n>)
     {
         if(n&) ans = ans*a;
         a = a*a;
         n>>=;
     }
     return ans;
 }
 int main()
 {
     int n;
     while(~scanf("%d%d",&n,&m))
     {
         if(n==) printf("%d\n",%m);
         else if(n==) printf("%d\n",%m);
         else if(n==) printf("%d\n",%m);
         else if(n==) printf("%d\n",%m);
         else
         {
             Mat t;
             t = multi(n-);
             int sol = ((t.mat[][]*)%m+(t.mat[][]*)%m+(t.mat[][]*)%m+(t.mat[][]*)%m)%m;
             printf("%d\n",sol);
         }
     }
     return ;
 }