[CSP-S模拟测试]:夜鹰与玫瑰（数学）

题目描述

红晕爬上了白玫瑰的花瓣，花刺还没有到达夜莺的心脏，玫瑰的心依旧苍白如终年不化的积雪。由生命铸就的玫瑰不允许存在一丝一毫的瑕疵，假设玫瑰的一片花瓣可以抽象成一个点，一朵玫瑰我们用一个$N\times M$的点阵表示，任意选择其中两个点可以构造出一条$"dead\ line"$。我们需要知道，对于一朵玫瑰，有多少条不同的$"dead\ line"$。两
条$"dead\ line"$不同当且仅当它们不重合，即两条$"dead\ line"$的交点数是有穷的。

---

输入格式

第一行一个正整数$T$表示数据组数，接下来$T$行，每行两个正整数$N,M$，意义如题。

---

输出格式

共$T$行，表示这一组数据的答案，答案对$2^{30}$取模。

---

样例

样例输入：

4
22
7 10
23 34
100 100

样例输出：

6
1111
139395
22791174

---

数据范围与提示

对于$40%$的数据T≤5,2≤N,M≤40$
对于另外$20%的数据T≤10,2≤N,M≤200$
对于$100%$的数据$T≤10,000,2≤N,M≤4,000$

---

题解

首先，解释一下题意，$"dead\ line"$是直线，而不是线段。

也就是对于下面这张图，所有的线段是：

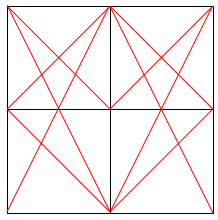
所以，我们先来考虑朴素算法。

那么我们发现，只有那些长和宽的$GCD$为$1$的矩形才有可能对答案造成贡献。

但是这样会有重复的，所以我们还要减去$GCD$为$2$的矩形的数量。

也就是说答案是：$\sum \limits_{i=1}^{n-1}\sum \limits_{j=1}^{m-1}[gcd(i,j)=1]((n-i)(m-j)-\max(n-2\times i,0)\times \max(m-2\times j,0))$

$60\%$算法：

每次暴力求上面那个式子。

时间复杂度：$\Theta(T\times n\times m)$。

期望得分：$60$分。

实际得分：$60$分。

$100\%$算法$1$：

通过前缀和预处理出来答案，然后$\Theta(1)$查询即可。

时间复杂度：$\Theta(T+4000\times 4000)$。

期望得分：$100$分。

实际得分：$100$分。

$100\%$算法$2$：

我也不太会，大概讲两句：

化简？上面那个式子：

$\sum \limits_{i=1}^{n-1}\sum \limits_{j=1}^{m-1}[gcd(i,j)=1]((n-i)(m-j)-\max(n-2\times i,0)\times \max(m-2\times j,0)) \\ =\sum \limits_{i=1}^{n-1}\sum \limits_{j=1}^{m-1}\sum \limits_{d|gcd(i,j)}\mu (d)\times ((n-i)(m-j)-\max(n-2\times i,0)\times \max(m-2\times j,0)) \\ =\sum \limits_{d=1}{n-1}\mu (d)\times \sum \limits_{i=1}^{\left \lfloor \dfrac{n-1}{d} \right \rfloor}\sum \limits_{j=1}^{\left \lfloor \dfrac{m-1}{d} \right \rfloor}\sum \limits_{x=1}^{n-i\times d}\sum \limits_{y=1}^{m-j\times d}[x\leqslant i\times d\ or\ y\leqslant j\times d] \\ =\sum \limits_{d=1}^{n-1}\mu (d)\times \sum \limits_{i=1}^{\left \lfloor \dfrac{n-1}{d} \right \rfloor}\sum \limits_{j=1}^{\left \lfloor \dfrac{m-1}{d} \right \rfloor}(\sum \limits_{x=1}^{n-i\times d}[x\leqslant i\times d]\times (m-j\times d)) \\ +(\sum \limits_{y=1}^{m-j\times d}[y\leqslant j\times d]\times (n-i\times d)) \\ -(\sum \limits_{x=1}^{n-i\times d}\sum \limits_{y=1}^{m-i\times d}[x\leqslant i\times d\ and\ y\leqslant j\times d]) \\ =\sum \limits_{d=1}^{n-1}\mu (d)\times (\sum \limits_{i=1}^{\left \lfloor \dfrac{n-1}{d}\right \rfloor}\sum \limits_{x=1}^{n-i\times d}[x\leqslant i\times d]\times \sum \limits_{j=1}^{\left \lfloor \dfrac{m-1}{d}\right \rfloor}(m-j\times d)) \\ +(\sum \limits_{j=1}^{\left \lfloor \dfrac{m-1}{d} \right \rfloor}\sum \limits_{y=1}^{m-j\times d}[y\leqslant j\times d]\times \sum \limits_{i=1}^{\left \lfloor \dfrac{n-1}{d}\right \rfloor}(n-i\times d)) \\ -\sum \limits_{i=1}^{\left \lfloor \dfrac{n-1}{d}\right \rfloor}\sum \limits_{x=1}^{n-i\times d}[x\leqslant i\times d]\times \sum \limits_{j=1}^{\left \lfloor \dfrac{m-1}{d}\right \rfloor}\sum \limits_{y=1}^{m-j\times d}[y\leqslant j\times d])$

希望我上面那么长的$\LaTeX$没有打错吧，毕竟它……

时间复杂度：$\Theta(T\times n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

$60\%$算法：

#include<bits/stdc++.h>
using namespace std;
int n,m;
unsigned int ans;
int main()
{
	int T;
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&n,&m);
		ans=0;
		for(int i=1;i<n;i++)
			for(int j=1;j<m;j++)
				if(__gcd(i,j)==1)
					ans+=(n-i)*(m-j)-(max((n-(i<<1)),0)*max(m-(j<<1),0));
		printf("%d\n",(n+m+(ans<<1))&1073741823);
	}
	return 0;
}

$100\%$算法$1$：

#include<bits/stdc++.h>
using namespace std;
int n,m;
pair<unsigned int,unsigned int> s[4001][4001];
int main()
{
	for(int i=1;i<=4000;i++)
		for(int j=1;j<=4000;j++)
		{
			s[i][j].first=(s[i-1][j].first+s[i][j-1].first-s[i-1][j-1].first+(__gcd(i,j)==1))&1073741823;
			s[i][j].second=(s[i-1][j].second+s[i][j-1].second-s[i-1][j-1].second+s[i][j].first-s[i>>1][j>>1].first)&1073741823;
		}
	int T;scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&n,&m);
		printf("%d\n",(n+m+(s[n-1][m-1].second<<1))&1073741823);
	}
	return 0;
}

$100\%$算法$2$：

#include<bits/stdc++.h>
using namespace std;
int n,m;
int phi[4001],mu[4001];
bool vis[4001];
unsigned int ans;
void pre_work()
{
	mu[1]=1;
	for(int i=2;i<=4000;i++)
	{
		if(!vis[i]){phi[++phi[0]]=i;mu[i]=-1;}
		for(int j=1;j<=phi[0];j++)
		{
			if(i*phi[j]>4000)break;
			vis[i*phi[j]]=1;
			if(!(i%phi[j])){mu[i*phi[j]]=0;break;}
			mu[i*phi[j]]=-mu[i];
		}
	}
}
int main()
{
	pre_work();
	int T;scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&n,&m);
		ans=0;
		for(int i=1;i<n;i++)
			ans+=2*mu[i]*(((n/(2*i)+1)*(n/(2*i))*i/2+n*((n-1)/i-n/(2*i))-((n-1)/i+n/(2*i)+1)*((n-1)/i-n/(2*i))*i/2)*(m*((m-1)/i)-((m-1)/i)*((m-1)/i+1)*i/2)+((m/(i*2)+1)*(m/(i*2))*i/2+m*((m-1)/i-m/(i*2))-((m-1)/i+m/(i*2)+1)*((m-1)/i-m/(i*2))*i/2)*(n*((n-1)/i)-((n-1)/i)*((n-1)/i+1)*i/2)-((n/(2*i)+1)*(n/(2*i))*i/2+n*((n-1)/i-n/(2*i))-((n-1)/i+n/(2*i)+1)*((n-1)/i-n/(2*i))*i/2)*((m/(i*2)+1)*(m/(i*2))*i/2+m*((m-1)/i-m/(i*2))-((m-1)/i+m/(i*2)+1)*((m-1)/i-m/(i*2))*i/2));
		printf("%d\n",(n+m+ans)&1073741823);
	}
	return 0;
}

---

rp++